1.1.1 数

1.1.1.1 自然数、整数和有理数

1. 定义和记号

正整数、负整数、分数和零统称为有理数. 相关的符号有 (参见第 439 页5.2.1,1.)

• 自然数集: $\mathbb{N}=\{0,1,2,3,\cdots \}$ ,

• 整数集: $\mathbb{Z}=\{\cdots ,-2,-1,0,1,2,\cdots \}$ ,

• 有理数集: $\mathbb{Q}=\left\{x\mid x=\frac{p}{q},p\in \mathbb{Z},q\in \mathbb{Z},q\ne 0\right\}$ .

自然数的概念来源于计数和排序. 自然数也被称为非负整数.

2. 有理数集的性质

• 有理数集是无限的.

• 有理数集是有序的,即任意给定两个不同的有理数 $a$ 和 $b$ ,总可以确定何者小,何者大.

• 有理数集是处处稠密的,即在任意两个不同的有理数 $a$ 和 $b\left(a<b\right)$ 之间,至少存在一个有理数 $c\left(a<c<b\right)$ . 从而,在任意两个不同的有理数之间,存在着无限多个其他的有理数.

3. 算术运算

算术运算 (加、减、乘、除) 可以在任意两个有理数之间执行, 结果仍是一个有理数. 唯一的例外是被零除,这是不可能的. 被写成 $a:0$ 的运算是无意义的,因为其不能得到任何结果: 如果 $a\ne 0$ ,那么不存在任何有理数 $b$ 能使 $b\cdot 0=a$ 成立; 而如果 $a=0$ ,则 $b$ 可以是任意有理数. 常常出现的表达式 $a:0=\mathrm{\infty }$ (无限大) 并不意味这一除法是可能的, 这只是一种记号, 其意义是: 当除数趋近于零, 而被除数不趋于零时, 那么商的绝对值 (大小) 可以大于任何有限的数.

4. 十进小数和连分数

每个有理数都可以表示为一个有限的或无限循环的十进小数, 或者表示为一个有限的连分数 (参见第 3 页 1.1.1.4).

5. 几何表示

在一条直线上确定一个原点作为零点, 确定一个正的方向作为定向, 确定一个长度单位 $l$ 作为量尺(参见第 149 页 2.17.1 和图 1.1),那么每一个有理数都对应此直线上一个确定的点. 该点具有坐标 $a$ ,并称为有理点. 该直线称为数轴. 因为有理数集处处稠密, 所以在任意两个有理点之间存在无限多个其他有理点.

1.1.1.2 无理数和超越数

有理数在运算中并不够用. 虽然有理数是处处稠密的, 但它却不能覆盖整个数轴. 例如,让单位正方形的对角线 $AB$ 绕点 $A$ 旋转,使 $B$ 落在数轴上的点 $K$ 处, 那么其坐标将不是任何有理数 (图 1.2).

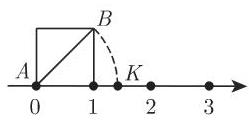
首先, 代数方程

$$x^n+a_{n-1}{x}^{n-1}+\cdots +a_{1}x+a_0=0\left(n>1\text{,整数; 方程系数均为整数}\right)$$

的非整数实根属于无理数, 这些根称为代数无理数.

无理数的引进使数轴上每个点都有一个与之对应的数. 一般教科书中对无理数都有精确的定义, 比如借助区间套的定义. 而这里则仅限于指出: 无理数填充了数轴上所有的非有理点, 每一个无理数都对应于数轴上的一个点, 每个无理数都可以用一个无限不循环的十进小数来表示.

$◼\mathbf{A}$: 代数无理数最简单的例子是方程 $x^n-a=0\left(a>0\right)$ 的非有理实根,记作 $\sqrt[n]{a}$ .

$◼\mathbf{B}$: $\sqrt[2]{2}=1.414\cdots ,\sqrt[3]{10}=2.154\cdots$ 是代数无理数.

不是代数无理数的无理数称为超越数.

$◼\mathbf{A}$: $\pi =3.141592\cdots ,\mathrm{e}=2.718281\cdots$ 是超越数.

$◼\mathbf{B}$: 形如 ${10}^n$ 以外的所有整数的以 10 为底的对数都是超越数.

二次方程

$$\begin{array}{}\text{(1.1b)}& x^2+a_{1}x+a_0=0(a_1,a_0\text{为整数})\end{array}$$

的非整数根称为二次无理数,它们具有 $\frac{a+b\sqrt{D}}{c}(a,b,c$ 均为整数, $c\ne 0;D>0$ ,是非平方数) 形式.

一条线段按黄金比例 $x/a=\left(a-x\right)/x$ (参见第 260 页 3.5.2.3,(3)) 所作的分割,当 $a=1$ 时导出方程 $x^2+x-1=0$ . 解 $x=\left(\sqrt{5}-1\right)/2$ 是一个二次无理数,其包含了无理数 $\sqrt{5}$ .

1.1.1.3 实数

有理数与无理数合起来形成实数集,记为 $\mathbb{R}$ .

1. 最重要的性质

实数集有下列重要性质 (亦可参见第 1 页 1.1.1.1, 2.):

• 无限性.

• 有序性.

• 处处稠密.

• 封闭性, 即数轴上任意一点都对应于一个实数. 有理数不具有这一性质.

2. 算术运算

任意两个实数之间都可以进行算术运算, 其结果仍为实数. 唯一的例外是不能被零除 (参见第 1 页 1.1.1.1, 3.). 实数可以进行乘方及其逆运算, 任一正实数都可以求其任意次开方根. 每一个正实数都有一个以除 1 外任意正数为底的对数.

数概念的进一步推广将导出复数的概念 (参见第 43 页 1.5).

3. 数区间

一个具有端点 $a$ 和 $b$ 的连通的实数集称为以 $a$ 和 $b$ 为端点的数区间,此处 $a<b,a$ 允许为 $-\mathrm{\infty },b$ 允许为 $+\mathrm{\infty }$ . 如果区间不包含端点,则称其为开区间,反之, 则称之为闭区间.

一个区间用置于括号内的端点来表示: 方括号表示闭区间, 圆括号表示开区间. 两个端点都不属内的开区间记为(a, b); 只有一个端点属内的半开 (半闭)区间记为 $[a,b)$ 或 $(a,b]$ ; 两个端点都属内的闭区间记为 $\left[a,b\right]$ . 有时会用 $a,b$ 替代(a, b)来标记开区间,类似地用 $[a,b$ 来替代 $[a,b)$ . 在图示情形,本书中以圆箭头表示区间的开端, 以实点表示其闭端.

1.1.1.4 连分数

连分数是具有套式结构的分数, 有理数和无理数都可以用它来表示并获得比十进小数更好的逼近 (参见第 1300 页 19.8.1.1 和第 5 页 $◼\mathbf{A}$ 与 $◼\mathbf{B}$ ).

1. 有理数

一个有理数的连分数是有限的表示式. 大于 1 的正有理数的连分数形如 (1.2)

$$\begin{array}{}\text{(1.2)}& \frac{p}{q}=a_0+\frac{1}{a_1+\frac{1}{a_2+\frac{1}{\ddots +\frac{1}{a_{n-1}+\frac{1}{a_n}}}}}.\end{array}$$

上式可以缩写为 $\frac{p}{q}=\left[a_0;a_1,a_2,\cdots ,a_n\right]$ ,其中 $a_k\ge 1\left(k=1,2,\cdots ,n\right)$ .

数 $a_k$ 可以借助欧几里得算法来计算:

$$\begin{array}{}\text{(1.3a)}& \frac{p}{q}=a_0+\frac{r_1}{q}\left(0<\frac{r_1}{q}<1\right),\end{array}$$$$\begin{array}{}\text{(1.3b)}& \frac{q}{r_1}=a_1+\frac{r_2}{r_1}\left(0<\frac{r_2}{r_1}<1\right),\end{array}$$$$\begin{array}{}\text{(1.3c)}& \frac{r_1}{r_2}=a_2+\frac{r_3}{r_2}\left(0<\frac{r_3}{r_2}<1\right),\end{array}$$$$\begin{array}{}\text{(1.3d)}& \frac{r_{n-2}}{r_{n-1}}=a_{n-1}+\frac{r_n}{r_{n-1}}\left(0<\frac{r_n}{r_{n-1}}<1\right),\end{array}$$$$\begin{array}{}\text{(1.3e)}& \frac{r_{n-1}}{r_n}=a_n\left(r_{n+1}=0\right).\end{array}$$$$◼\frac{61}{27}=2+\frac{7}{27}=2+\frac{1}{3+\frac{6}{7}}=2+\frac{1}{3+\frac{1}{1+\frac{1}{6}}}=\left[2;3,1,6\right].$$

2. 无理数

无理数的连分数是不中断的,它们称为无限连分数,记作 $\left[a_0;a_1,a_2,\cdots \right]$ .

如果在一个连分数表示式中有某个 $a_k$ 重复出现,就称此分数为循环连分数或循环链分数(recurring chain franction). 每个循环连分数都表示一个二次无理数, 反之, 每个二次无理数都可以表示为循环连分数.

$◼\sqrt{2}=1.4142135\cdots$ 是一个二次无理数,它有循环连分数表示式 $\sqrt{2}=[1;2,2$ , $2,\cdots ]$ .

3. 实数的逼近

如果 $\alpha =\left[a_0;a_1,a_2,\cdots \right]$ 是任一实数,则每一个有限连分数

$$\begin{array}{}\text{(1.4)}& {\alpha }_k=\left[a_0;a_1,a_2,\cdots ,a_k\right]=\frac{p}{q}\end{array}$$

表示 $\alpha$ 的一个逼近. 连分数 ${\alpha }_k$ 称为 $\alpha$ 的 $k$ 阶逼近. 它可以通过递推公式

$$\begin{array}{}\text{(1.5)}& {\alpha }_k=\frac{p_k}{q_k}=\frac{a_k{p}_{k-1}+p_{k-2}}{a_k{q}_{k-1}+q_{k-2}}\left(k\ge 1;p_{-1}=1,p_0=a_0;q_{-1}=0,q_0=1\right)\end{array}$$

来计算. 根据刘维尔逼近定理, 下列误差估计式成立

$$\begin{array}{}\text{(1.6)}& \left|\alpha -{\alpha }_k\right|=\left|\alpha -\frac{p_k}{q_k}\right|<\frac{1}{q_k^2}\end{array}$$

还可以进一步证明: 该近似式以渐增的精度上下交替地逼近实数 $\alpha$ . 当 (1.4) 中的 $a_i\left(i=1,2,\cdots ,k\right)$ 具有大数值时,近似式迅速收敛于 $\alpha$ . 因此,对于数 $\left[1;1,1,\cdots \right]$ 而言, 收敛是最差的.

$◼\mathbf{A}$: 通过 (1.3a)-(1.3e) 可以从 $\pi$ 的十进小数表示得到其连分数表示 $\pi =[3;7,15$ , $1,292,\cdots ]$ . 相应的近似值 (1.5) 及根据 (1.6) 得到的误差估计为: ${\alpha }_1=\frac{22}{7}$ 和 $\left|\pi -{\alpha }_1\right|<\frac{1}{7^2}\approx 2\cdot {10}^{-2},{\alpha }_2=\frac{333}{106}$ 和 $\left|\pi -{\alpha }_2\right|<\frac{1}{{106}^2}\approx 9\cdot {10}^{-5},{\alpha }_3=\frac{355}{113}$ 和 $\left|\pi -{\alpha }_3\right|<\frac{1}{{113}^2}\approx 8\cdot {10}^{-5}$ . 实际误差更小些,对 ${\alpha }_1$ 而言小于 $1.3\cdot {10}^{-3}$ ,对 ${\alpha }_2$ 而言小于 $8.4\cdot {10}^{-5}$ ,对 ${\alpha }_3$ 而言小于 $2.7\cdot {10}^{-7}$ . 近似值 ${\alpha }_1,{\alpha }_2$ 和 ${\alpha }_3$ 是对 $\pi$ 的比相应位数的小数表示更好的逼近.

$◼\mathbf{B}$: 黄金分割公式 $x/a=\left(a-x\right)/x$ (参见第 260 页 3.5.2.3,(3)) 可由以下两个连分数来表示: $x=a\left[1;1,1,\cdots \right]$ 和 $x=\frac{a}{2}\left(1+\sqrt{5}\right)=\frac{a}{2}\left(1+\left[2;4,4,4,\cdots \right]\right)$ . 第一个表示式中近似值 ${\alpha }_4$ 的精确度为 $0.018a$ ,第二个表示式的精确度则达到 $0.000001a$ .

1.1.1.5 可公度性

一个表示式中如果两个数 $a$ 和 $b$ 分别为第三个数 $c$ 的整数倍,则称它们为可公度的,即可以被同一个数量度. 由 $a=mc,b=nc\left(m,n\in \mathbb{Z}\right)$ 可得

$$\begin{array}{}\text{(1.7)}& \frac{a}{b}=x\left(x\text{ 是有理数 }\right),\end{array}$$

否则就称 $a$ 和 $b$ 为不可公度的.

$◼\mathbf{A}$:一个正方形边长与其对角线长是不可公度的,因为它们的比是无理数 $\sqrt{2}$ .

$◼\mathbf{B}$:黄金分割线段是不可公度的,因为它们的比包含有无理数 $\sqrt{5}$ (参见第 260 页 $3.5.2.3,\left(3\right))$ . 因此,一个正五边形的边长与其对角线长是不可公度的 (参见第 182 页 3.1.5.3). 现在认为梅塔蓬图姆的希帕索斯 (Hippasos of Metapontum, 公元前 450 年) 正是通过这一例子发现了无理数.