4.4.1 四元数

4.4.1.1 定义和表示

1. 虚数单位

四元数是形如

\begin{matrix} (4.106) & w + i x + j y + k z \end{matrix}

的广义复数,其中 $w, x, y, z$ 是实数, $i, j, k$ 是广义虚数单位,它们满足下列乘法法则:

\begin{matrix} (4.107) & i^{2} = j^{2} = k^{2} = - 1, i j = k = - ji, jk = i = - kj, ki = j = - ik, \end{matrix}

广义虚数单位的乘法法则见所附的乘法表. 这个法则也可用图 4.4 中的圈表示. 按箭头方向做乘法得到正号, 反箭头方向产生负号.

乘法表

	i	$j$	$k$
i	-1	$k$	-j
j	k	-1	i
$k$	$j$	$- i$	-1

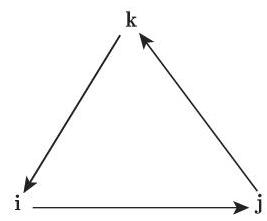
019363af-d8ae-7006-ac42-15a9aafbc2ce_27_687_737_267_221_0.jpg

因此, 乘法不可交换, 但可结合. 为纪念哈密顿, 将定义了四元数乘法的四维欧氏向量空间 $R^{4}$ 记作 $H$ . 四元数形成一个代数,称作四元数除环.

2. 四元数的表示

四元数有不同的表示:

作为超复数 $q = w + i x + j y + k z = q_{0} + \underset{―}{q}$ ,其中标量部分 $q_{0} = Sc q$ ,向量部分 $\underset{―}{q} = Vec q .$
作为由数 $w \in R$ 和向量 ${(x, y, z)}^{T} \in R^{3}$ 组成的四维向量 $q = {(w, x, y, z)}^{T} =$ ${(q_{0}, \underset{―}{q})}^{T}$ .
三角式 $q = r (\cos φ + {\underset{―}{n}}_{\underset{―}{q}} \sin φ)$ ,其中 $r = | q | = \sqrt{w^{2} + x^{2} + y^{2} + z^{2}}$ 是 $R^{4}$ 中四维向量的长度,并且 $\cos φ = \frac{w}{| q |}$ ,以及 ${\underset{―}{n}}_{\underset{―}{q}} = \frac{1}{| {(x, y, z)}^{T} |} {(x, y, z)}^{T} \cdot {\underset{―}{n}}_{\underset{―}{q}}$ 是 $R^{3}$ 中与 $\underset{―}{q}$ 有关的单位向量.

注四元数的乘法法则不同于通常在 $R^{3}$ 和 $R^{4}$ 中引进的法则 (参见 (4.109b), (4.114), (4.115)).

3. 超复数与三角式间的关系

如果 $| \underset{―}{q} | \neq 0$ ,那么

\begin{matrix} (4.108a) & q = q_{0} + \underset{―}{q} = | q | (\frac{q_{0}}{| q |} + \frac{q}{| q |}) = | q | (\frac{q_{0}}{| q |} + \frac{q}{| \underset{―}{q} |} \frac{| \underset{―}{q} |}{| q |}) = r (\cos φ + \underset{―}{n_{\underset{―}{q}}} \sin φ) \end{matrix}

如果 $| \underset{―}{q} | = 0$ ,那么当 $q_{0} \neq 0$ 时有

\begin{matrix} (4.108b) & q = q_{0} = | q_{0} | \frac{q_{0}}{| q_{0} |} = {\begin{cases} | q_{0} | = | q_{0} | \cos 0, & q_{0} > 0, \\ | q_{0} | (- 1) = | q_{0} | \cos π, & q_{0} < 0. \end{cases} \end{matrix}

4. 纯四元数

纯四元数的标量部分为零: $q_{0} = 0$ . 纯四元数的集合记作 $H_{0}$ . 我们经常将纯四元数 $\underset{―}{q}$ 等同于几何向量 $\vec{q} \in R^{3}$ ,即

\begin{matrix} (4.109a) & q = q_{0} + {\begin{cases} \underset{―}{q}, & 若 \underset{―}{q} 表示纯四元数, \\ \vec{q}, & 若 \underset{―}{q} 解释为几何向量. \end{cases} \end{matrix}

对于 $\underset{―}{p}, \underset{―}{q} \in H_{0}$ ,乘法法则是

\begin{matrix} (4.109b) & \underset{―}{p} \underset{―}{q} = - \vec{p} \cdot \vec{q} + \vec{p} \times \vec{q}, \end{matrix}

其中 $\cdot$ 和 $\times$ 分别表示 $R^{3}$ 中的点积和叉积. (4.109b) 的结果解释为一个四元数.

令 $\nabla = \frac{\partial}{\partial x} \vec{i} + \frac{\partial}{\partial y} \vec{j} + \frac{\partial}{\partial z} \vec{k}$ 是纳勃拉算子 (参见第 933 页 13.2.6.1),并令 $\vec{v} = v_{1} (x, y, z) \vec{i} + v_{2} (x, y, z) \vec{j} + v_{3} (x, y, z) \vec{k}$ 是一个向量场. 这里 $\vec{i}, \vec{j}, \vec{k}$ 是笛卡儿坐标系中平行于坐标轴的单位向量. 如果 $\nabla$ 和 $\vec{v}$ 解释为纯四元数,那么依据 (4.107), 它们的积是

\nabla \vec{v} = - \frac{\partial v_{1}}{\partial x} - \frac{\partial v_{2}}{\partial y} - \frac{\partial v_{3}}{\partial z} + \vec{i} (\frac{\partial v_{3}}{\partial y} - \frac{\partial v_{2}}{\partial z})

+ \vec{j} (\frac{\partial v_{1}}{\partial z} - \frac{\partial v_{3}}{\partial x}) + \vec{k} (\frac{\partial v_{2}}{\partial x} - \frac{\partial v_{1}}{\partial y}) .

这个四元数可以在向量解释下, 写成

\nabla \vec{v} = - div \tilde{v} + rot \tilde{v}

但这个结果应该看作四元数.

5. 单位四元数

如果 $| q | = 1$ ,那么四元数 $q$ 是单位四元数. 单位四元数的集合记作 $H_{1} . H_{1}$ 是所谓乘法李群. 集合 $H_{1}$ 可以等同于三维球 $S^{3} = {\underset{―}{x} \in R^{4} : | \underset{―}{x} | = 1}$ .

4.4.1.2 四元数的矩阵表示

1. 实矩阵

如果数 1 等同于恒等矩阵

\begin{matrix} (4.110a) & 1 ≜ (\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}) \end{matrix}

以及

i ≜ (\begin{matrix} 0 & - 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & - 1 & 0 \end{matrix}), j ≜ (\begin{matrix} 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & - 1 \\ 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \end{matrix}), k ≜ (\begin{matrix} 0 & 0 & 0 & 1 \\ 0 & 0 & - 1 & 0 \\ 0 & 1 & 0 & 0 \\ - 1 & 0 & 0 & 0 \end{matrix}),

(4.110b)

那么四元数 $q = w + i x + j y + k z$ 可以表示为矩阵

\begin{matrix} (4.110c) & q ≜ (\begin{matrix} w & - x & - y & z \\ x & w & - z & - y \\ y & z & w & x \\ - z & y & - x & w \end{matrix}) \end{matrix}

2. 复矩阵

四元数可以通过复矩阵

\begin{matrix} (4.111a) & i ≜ (\begin{matrix} 0 & - i \\ - i & 0 \end{matrix}), j ≜ (\begin{matrix} 0 & - 1 \\ 1 & 0 \end{matrix}), k ≜ (\begin{matrix} - i & 0 \\ 0 & i \end{matrix}) \end{matrix}

表示. 于是

\begin{matrix} (4.111b) & q = w + i x + j y + k z ≜ (\begin{matrix} w - i z & i x - y \\ i x + y & w + i z \end{matrix}) . \end{matrix}

注 (1) 在方程 (4.111a, 4.111b) 的右边, i 表示复数的虚数单位.

(2) 四元数的矩阵表示并不唯一, 即有可能给出与 (4.110b, 4.110c) 及 (4.111a, 4.111b) 不同的表示.

3. 共轭与逆元素

四元数 $q = w - i x + j y + k z$ 的共轭是四元数

\begin{matrix} (4.112a) & \bar{q} = w - i x - j y - k z . \end{matrix}

显然,

\begin{matrix} (4.112b) & {| q |}^{2} = q \bar{q} = \bar{q} q = w^{2} + x^{2} + y^{2} + z^{2} . \end{matrix}

因此每个四元数 $q \in H ∖ {0}$ 都有逆元素

\begin{matrix} (4.112c) & q^{- 1} = \frac{\bar{q}}{{| q |}^{2}} . \end{matrix}

4.4.1.3 计算法则

1. 加法和减法

两个或多个四元数的加法和减法定义为

q_{1} + q_{2} - q_{3} + \dots

= (w_{1} + i x_{1} + j y_{1} + k z_{1}) + (w_{2} + i x_{2} + j y_{2} + k z_{2})

- (w_{3} + i x_{3} + j y_{3} + k z_{3}) + \dots

= (w_{1} + w_{2} - w_{3} + \dots) + i (x_{1} + x_{2} - x_{3} + \dots)

\begin{matrix} (4.113) & + j (y_{1} + y_{2} - y_{3} + \dots) + k (z_{1} + z_{2} - z_{3} + \dots) . \end{matrix}

四元数的加减与 $R^{4}$ 中的向量或矩阵的加减相同.

2. 乘法

乘法是结合的, 所以

q_{1} q_{2} = (w_{1} + i x_{1} + j y_{1} + k z_{1}) (w_{2} + i x_{2} + j y_{2} + k z_{2})

= (w_{1} w_{2} - x_{1} x_{2} - y_{1} y_{2} - z_{1} z_{2}) + i (w_{1} x_{2} + w_{2} x_{1} + y_{1} z_{2} - z_{1} y_{2})

+ j (w_{1} y_{2} + w_{2} y_{1} + z_{1} x_{2} - z_{2} x_{1}) + k (w_{1} z_{2} + w_{2} z_{1} + x_{1} y_{2} - x_{2} y_{1}) .

(4.114)

应用通常 $R^{3}$ 中的向量积 (参见第 247 页 3.5.1.5),它可以写成

\begin{matrix} (4.115) & q_{1} q_{2} = (q_{01} + {\underset{―}{q}}_{1}) (q_{02} + {\underset{―}{q}}_{2}) = q_{01} q_{02} - {\vec{q}}_{1} \cdot {\vec{q}}_{2} + {\vec{q}}_{1} \times {\vec{q}}_{2}, \end{matrix}

其中 ${\vec{q}}_{1} \cdot {\vec{q}}_{2}$ 和 ${\vec{q}}_{1} \times {\vec{q}}_{2}$ 是向量 ${\vec{q}}_{1}, {\vec{q}}_{2} \in R^{3}$ 的点积和叉积. 其次是 $R^{3}$ 等同于纯四元数的空间 $H_{0}$ .

注四元数的乘法不可交换!

乘积 $q_{1} q_{2}$ 对应于矩阵 $L_{q_{1}}$ 与向量 $q_{2}$ 的矩阵乘法,并且它等于矩阵 $R_{q_{2}}$ 与向量 $q_{1}$ 的积:

q_{1} q_{2} = L_{q_{1}} q_{2} = (\begin{matrix} w_{1} & - x_{1} & - y_{1} & - z_{1} \\ x_{1} & w_{1} & - z_{1} & y_{1} \\ y_{1} & z_{1} & w_{1} & - x_{1} \\ z_{1} & - y_{1} & x_{1} & w_{1} \end{matrix}) (\begin{array}{l} w_{2} \\ x_{2} \\ y_{2} \\ z_{2} \end{array})

\begin{matrix} (4.116) & = R_{q_{2}} q_{1} = (\begin{matrix} w_{2} & - x_{2} & - y_{2} & - z_{2} \\ x_{2} & w_{2} & z_{2} & - y_{2} \\ y_{2} & - z_{2} & w_{2} & x_{2} \\ z_{2} & y_{2} & - x_{2} & w_{2} \end{matrix}) (\begin{array}{l} w_{1} \\ x_{1} \\ y_{1} \\ z_{1} \end{array}) \end{matrix}

3. 除法

两个四元数相除是基于乘法定义的: $q_{1}, q_{2} \in H, q_{2} \neq 0$ ,

\begin{matrix} (4.117) & \frac{q_{1}}{q_{2}} := q_{1} q_{2}^{- 1} = q_{1} \frac{{\bar{q}}_{2}}{{| q_{2} |}^{2}} . \end{matrix}

因子的次序是重要的.

令 $q_{1} = 1 + j, q_{2} = \frac{1}{\sqrt{2}} (1 - k)$ ,那么 $| q_{2} | = 1, {\bar{q}}_{2} = \frac{1}{\sqrt{2}} (1 + k)$ ,因而

\frac{q_{1}}{q_{2}} := q_{1} \frac{{\bar{q}}_{2}}{{| q_{2} |}^{2}} = \frac{1}{\sqrt{2}} (1 + i + j + k) \neq \frac{{\bar{q}}_{2}}{{| q_{2} |}^{2}} q_{1} = \frac{1}{\sqrt{2}} (1 - i + j + k) .

4. 广义棣莫弗公式

设 $q \in H, q = q_{0} + \underset{―}{q} = r (\cos φ + {\underset{―}{n}}_{\underset{―}{q}} \sin φ)$ ,其中 $r = | q |, φ = \arccos \frac{q_{0}}{| q |}, \cos φ =$ $\frac{q_{0}}{| q |}, \sin φ = \frac{| q |}{| q |}$ ,那么对于任何 $k \in N :$

\begin{matrix} (4.118) & q^{k} = r^{k} e^{\underset{―}{n} \cdot {\underset{―}{q}}^{k φ}} = r^{k} (\cos (k φ) + {\underset{―}{n}}_{\underset{―}{q}} \sin (k φ)) . \end{matrix}

5. 指数函数

对于 $q = q_{0} + \underset{―}{q} \in H$ ,它的指数函数定义为

\begin{matrix} (4.119) & e^{q} = \sum_{k = 0}^{\infty} \frac{q^{k}}{k!} = e^{q_{0}} (\cos | \underset{―}{q} | + {\underset{―}{n}}_{\underset{―}{q}} \sin | \underset{―}{q} |) . \end{matrix}

指数函数的性质对于 $q \in H$ ,有

\begin{matrix} (4.120a) & e^{- q} e^{q} = 1, \end{matrix}

$e^{q} \neq 0$ (4.120b)

\begin{matrix} (4.120c) & e^{q} = e^{q_{0} + \underset{―}{q}} = e^{q_{0}} e^{\underset{―}{q}}, \end{matrix}

$e^{\underset{―}{n} {\underset{―}{q}}^{π}} = - 1$ ,特别 $e^{i π} = e^{j π} = e^{k π} = - 1$ .(4.120d)

对于单位四元数 $u$ 和 $ϑ \in R : e^{ϑ u} = \cos ϑ + u \sin ϑ$ .(4.120e)

如果 $q_{1} q_{2} = q_{2} q_{1}$ ,那么 $e^{q_{1} + q_{2}} = e^{q_{1}} e^{q_{2}}$ . 但是,由 $e^{q_{1} + q_{2}} = e^{q_{1}} e^{q_{2}}$ 推不出 $q_{1} q_{2} = q_{2} q_{1}$

因为 $(i π) (j π) = k π^{2} \neq - k π^{2} = (j π) (i π)$ ,所以也有

e^{i π} e^{j π} = (\cos π) (\cos π) = (- 1) (- 1) = 1,

但是,

e^{i π + j π} = (\cos (\sqrt{2} π) + \frac{i + j}{\sqrt{2}} \sin (\sqrt{2} π)) \neq 1.

6. 三角函数

对于 $q \in H$ ,令

\begin{matrix} (4.121) & \cos q := \frac{1}{2} (e^{\underset{―}{n} {\underset{―}{q}}^{q}} + e^{- \underset{―}{n} {\underset{―}{q}}^{q}}), \sin q := - \underset{―}{n_{\underset{―}{q}}} (e^{\underset{―}{n} {\underset{―}{q}}^{q}} - e^{- \underset{―}{n} {\underset{―}{q}}^{q}}) . \end{matrix}

$\cos q$ 是偶函数,与此相反, $\sin q$ 是奇函数.

加法公式对于任何 $q = q_{0} + \underset{―}{q} \in H$ ,有

\begin{matrix} (4.122) & \cos q = \cos q_{0} \cos \underset{―}{q} - \sin q_{0} \sin \underset{―}{q}, \sin q = \sin q_{0} \cos \underset{―}{q} + \cos q_{0} \sin \underset{―}{q} . \end{matrix}

7. 双曲线函数

对于 $q \in H$ ,令

\begin{matrix} (4.123) & \cosh q := \frac{1}{2} (e^{q} + e^{- q}), \sinh q := - \underset{―}{n_{\underset{―}{q}}} (e^{q} - e^{- q}) . \end{matrix}

$\cosh q$ 是偶函数,与此相反, $\sinh q$ 是奇函数.

加法公式对于任何 $q = q_{0} + \underset{―}{q} \in H$ 有

$\cosh q = \cosh q_{0} \cos \underset{―}{q} - \sinh q_{0} \sinh \underset{―}{q}, \sinh q = \sinh q_{0} \cos \underset{―}{q} + \cosh q_{0} \sinh \underset{―}{q}$ (4.124)

8. 对数函数

对于 $q = q_{0} + \underset{―}{q} = r (\cos φ + \underset{―}{n_{q}} \sin φ) \in H$ ,以及 $k \in Z$ ,对数函数的第 $k$ 个分支定义为

\begin{matrix} (4.125) & \log_{k} q := {\begin{cases} \ln r + {\underset{―}{n}}_{\underset{―}{q}} (φ + 2 k π), & | \underset{―}{q} | \neq 0, 或 | \underset{―}{q} | = 0, 并且 q_{0} \\ 无定义, & | \underset{―}{q} | \neq 0, 并且 q_{0} < 0. \end{cases} \end{matrix}

对数函数的性质

$e^{\log_{k} q} = q$ ,对于任何使得 $\log_{k} q$ 有定义的 $q \in H$ ,(4.126a)

$\log_{0} e^{q} = q$ ,对于任何使得 $| \underset{―}{q} | \neq (2 l + 1) π (l \in Z)$ 的 $q \in H$ ,(4.126b)

$\log_{k} 1 = 0,$ (4.126c)

$\log_{0} i = \frac{π}{2} i, \log_{0} j = \frac{π}{2} j, \log_{0} k = \frac{π}{2} k .$ (4.126d)

在 $\log q_{1}$ 与 $\log q_{2}$ 或 $q_{1}$ 与 $q_{2}$ 交换的情形下,则当适当定义 $k$ 时,下面熟知的等式 (4.127) 成立:

\begin{matrix} (4.127) & \log (q_{1} q_{2}) = \log q_{1} + \log q_{2} . \end{matrix}

对于单位四元数 $q \in H_{1}$ ,有 $| q | = 1$ 和 $q = \cos φ + \underset{―}{n_{q}} \sin φ$ ,因而

\begin{matrix} (4.128) & \log q := \log_{0} q = \underset{―}{n_{\underset{―}{q}}} φ (当 q \neq - 1) . \end{matrix}

9. 幂函数

设 $q \in H$ 及 $α \in R$ ,则

\begin{matrix} (4.129) & q^{α} := e^{α \log q} . \end{matrix}

4.4.1 四元数 ​

4.4.1.1 定义和表示 ​

1. 虚数单位 ​

2. 四元数的表示 ​

3. 超复数与三角式间的关系 ​

4. 纯四元数 ​

5. 单位四元数 ​

4.4.1.2 四元数的矩阵表示 ​

1. 实矩阵 ​

2. 复矩阵 ​

3. 共轭与逆元素 ​

4.4.1.3 计算法则 ​

1. 加法和减法 ​

2. 乘法 ​

3. 除法 ​

4. 广义棣莫弗公式 ​

5. 指数函数 ​

6. 三角函数 ​

7. 双曲线函数 ​

8. 对数函数 ​