17.1.3 离散动力系统

17.1.3.1 稳态、周期轨和极限集

1. 平衡点类型

当 $M\subset {\mathbb{R}}^n$ 时,设 $x_0$ 是方程 (17.3) 的平衡点. 在特定假设下,迭代系统 (17.3) 在 $x_0$ 附近的局部行为可由变分方程 $y_{t+1}=D\phi \left(x_0\right)y_t,t\in \mathrm{\Gamma }$ 刻画. 若 $D\left(x_0\right)$ 没有特征值 ${\lambda }_i$ 满足 $\left|{\lambda }_i\right|=1$ ,则类似于微分方程情形,平衡点 $x_0$ 称为双曲平衡点. 双曲平衡点 $x_0$ 是(m, k)型的,如果 $Df\left(x_0\right)$ 在复单位圆周内恰有 $m$ 个特征值,在复单位圆周外恰有 $k=n-m$ 个特征值.(m, k)型双曲平衡点,当 $m=n$ 时,称为汇; 当 $k=n$ 时,称为源; 当 $m>0$ 且 $k>0$ 时,称为鞍点. 汇是渐近稳定的; 源和鞍点是不稳定的 (离散系统一阶近似的稳定性定理).

2. 周期轨

令 $\gamma \left(x_0\right)=\left\{{\phi }^k\left(x_0\right),k=0,\cdots ,T-1\right\}$ 是方程 (17.3) 的 $T$ 周期解 $\left(T\ge 2\right)$ . 若 $x_0$ 是映射 ${\phi }^T$ 的双曲平衡点,则 $\gamma \left(x_0\right)$ 称为双曲的.

矩阵 $D{\phi }^T\left(x_0\right)=D\phi \left({\phi }^{T-1}\left(x_0\right)\right)\cdots D\phi \left(x_0\right)$ 称为单值矩阵, $D{\phi }^T\left(x_0\right)$ 的特征值 ${\rho }_i$ 是 $\gamma \left(x_0\right)$ 的乘子.

若 $\gamma \left(x_0\right)$ 所有乘子 ${\rho }_i$ 的绝对值都小于 1,则周期轨 $\gamma \left(x_0\right)$ 是渐近稳定的.

3. $\omega$ 极限集的性质

当 $M={\mathbb{R}}^n$ 时,系统 (17.3) 的任意 $\omega$ 极限集是闭集,并且 $\omega \left(\phi \left(x\right)\right)=\omega \left(x\right)$ . 若正半轨 ${\gamma }^{+}\left(x\right)$ 有界,则 $\omega \left(x\right)\ne \varnothing$ 并且 $\omega \left(x\right)$ 是 $\phi$ 的不变集. 对于 $\alpha$ 极限集,也有类似的性质.

假设在 $\mathbb{R}$ 上 $\phi \left(x\right)=-x$ ,此时差分方程为 $x_{t+1}=-x_t,t=0,\pm 1,\cdots$ 显然,当 $x=1$ 时,有 $\omega \left(1\right)=\{1,-1\},\omega \left(\phi \left(1\right)\right)=\omega \left(-1\right)=\omega \left(1\right)$ ,并且 $\phi \left(\omega \left(1\right)\right)=\omega \left(1\right)$ . 注意: $\omega \left(1\right)$ 不是连通集,这与微分方程情形不同.

17.1.3.2 不变流形

1. 分界面

设 $x_0$ 是系统 (17.3) 的平衡点. 那么, $W^s\left(x_0\right)=\{y\in M:{\phi }^i\left(y\right)\to x_0$ 当 $i\to$ $+\mathrm{\infty }\}$ 称为稳定流形, $W^u\left(x_0\right)=\left\{y\in M:{\phi }^i\left(y\right)\to x_0\text{,当}i\to -\mathrm{\infty }\right\}$ 称为不稳定流形. 稳定流形和不稳定流形也称为分界面.

2. 阿达马-佩龙 (Hadamard-Perron) 定理

阿达马-佩龙定理给出了当 $M\subset {\mathbb{R}}^n$ 时,离散系统分界面的重要性质.

若 $x_0$ 是系统 (17.3) 中(m, k)型双曲平衡点,则 $W^s\left(x_0\right)$ 和 $W^u\left(x_0\right)$ 分别是 $m$ 维和 $k$ 维的广义 $C^r$ 光滑曲面,其局部类似 $C^r$ 光滑基本曲面. 若当 $i\to +\mathrm{\infty }$ 或对应地, $i\to -\mathrm{\infty }$ 时,方程 (17.3) 中一条轨道不收敛到 $x_0$ ,则当 $i\to +\mathrm{\infty }$ 或对应地, $i\to -\mathrm{\infty }$ 时,该轨道会离开 $x_0$ 的某个充分小的邻域. 曲面 $W^s\left(x_0\right)$ 和 $W^u\left(x_0\right)$ 在 $x_0$ 处分别相切于系统 $y_{i+1}=D\phi \left(x_0\right)y_i$ 的稳定向量子空间

$$E^s=\left\{y\in {\mathbb{R}}^n:{\left[D\phi \left(x_0\right)\right]}^{i}y\to 0\text{ 当 }i\to +\mathrm{\infty }\right\}$$

和不稳定向量子空间

$$E^u=\left\{y\in {\mathbb{R}}^n:{\left[D\phi \left(x_0\right)\right]}^{i}y\to 0\text{ 当 }i\to -\mathrm{\infty }\right\}$$

考虑埃农映射族导出的离散动力系统

$$\begin{array}{}\text{(17.23)}& x_{i+1}=x_i^2+y_i-2,y_{i+1}=x_i,i\in \mathbb{Z}.\end{array}$$

系统 (17.23) 的两个双曲平衡点是 $P_1=\left(\sqrt{2},\sqrt{2}\right)$ 和 $P_2=\left(-\sqrt{2},-\sqrt{2}\right)$ .

$P_1$ 局部稳定流形和不稳定流形的确定: 利用变量替换 $x_i={\xi }_i+\sqrt{2},y_i=$ ${\eta }_i+\sqrt{2}$ ,系统 (17.23) 转化为 ${\xi }_{i+1}={\xi }_i^2+2\sqrt{2}{\xi }_i+{\eta }_i,{\eta }_{i+1}={\xi }_i$ ,其平衡点为 (0,0). 雅可比矩阵 $Df\left(\left(0,0\right)\right)$ 对应于特征值 ${\lambda }_{1,2}=\sqrt{2}\pm \sqrt{3}$ 的特征向量为 $a_1=$ $\left(\sqrt{2}+\sqrt{3},1\right)$ 和 $a_2=\left(\sqrt{2}-\sqrt{3},1\right)$ . 于是, $E^s=\left\{t{a}_2,t\in \mathbb{R}\right\},E^u=\left\{t{a}_1,t\in \mathbb{R}\right\}$ . 假设 $W_{\text{loc }}^u\left(\left(0,0\right)\right)=\{\left(\xi ,\eta \right):\eta =\beta \left(\xi \right),\left|\xi \right|<\mathrm{\Delta },\beta :\left(-\mathrm{\Delta },\mathrm{\Delta }\right)\to \mathbb{R}$ 可微 $\}$ ,我们来确定 $\beta$ 的幂级数形式 $\beta \left(\xi \right)=\left(\sqrt{3}-\sqrt{2}\right)\xi +k{\xi }^2+\cdots$ . 由 $\left({\xi }_i,{\eta }_i\right)\in W_{\text{loc }}^u\left(\left(0,0\right)\right)$ , 得 $\left({\xi }_{i+1},{\eta }_{i+1}\right)\in W_{\text{loc }}^u\left(\left(0,0\right)\right)$ . 由此可导出关于 $\beta$ 展开系数的方程,其中 $k<0$ . 图 17.11(a) 给出了稳定流形和不稳定流形的形状.

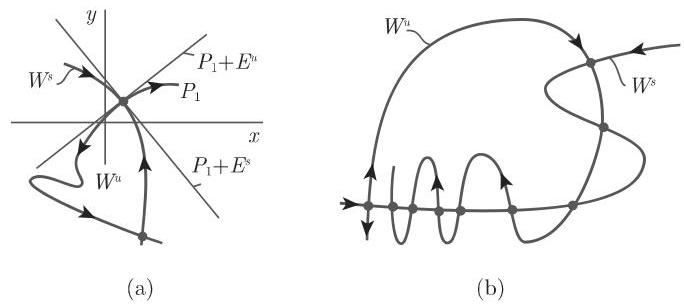
3. 横截同宿点

系统 (17.3) 中双曲平衡点 $x_0$ 的分界面 $W^s\left(x_0\right)$ 和 $W^u\left(x_0\right)$ 可能相交. 若交集 $W^s\left(x_0\right)\cap W^u\left(x_0\right)$ 是横截的,则任意点 $y\in W^s\left(x_0\right)\cap W^u\left(x_0\right)$ 称为横截同宿点.

事实上,若 $y$ 是横截同宿点,则可逆系统 (17.3) 的轨道 $\left\{{\phi }_i\left(y\right)\right\}$ 仅由这些横截同宿点构成.

17.1.3.3 离散系统的拓扑共轭

1. 定义

除了系统 (17.3), 假设还有一个离散系统

$$\begin{array}{}\text{(17.24)}& x_{t+1}=\psi \left(x_t\right),\end{array}$$

其中, $N\subset {\mathbb{R}}^n,\psi :N\to N$ 是连续映射 ( $M$ 和 $N$ 可以是一般度量空间). 离散系统 (17.3) 和 (17.24) (或映射 $\phi$ 和 $\psi$ ) 称为拓扑共轭,如果存在同胚映射 $h:M\to N$ 使得 $\phi =h^{-1}\circ \psi \circ h$ . 若离散系统 (17.3) 和 (17.24) 是拓扑共轭的,则同胚映射 $h$ 将系统 (17.3) 的轨道映射为方程 (17.24) 的轨道.

2. 格罗布曼-哈特曼定理

设系统 (17.3) 中 $\phi :{\mathbb{R}}^n\to {\mathbb{R}}^n$ 是同胚映射, $x_0$ 是系统 (17.3) 的双曲平衡点. 那么,在 $x_0$ 的某个邻域内,系统 (17.3) 与其线性化方程 $y_{t+1}=D\phi \left(x_0\right)y_t$ 拓扑共轭.