17.1.1 动力系统

17.1.1.1 基本概念

1. 动力系统与轨道的概念

动力系统是数学上的一个概念, 描述了物理、生物或其他现实系统随时间演化的情况. 设 $M$ 为相空间, $t$ 为时间参数,定义动力系统是一个单参数映射族 ${\phi }^t$ : $M\to M$ . 在下面的讨论中,相空间一般取 ${\mathbb{R}}^n$ ,或 ${\mathbb{R}}^n$ 的某一子集,或一个度量空间. 时间参数 $t$ 的取值范围是 $\mathbb{R}$ (时间连续系统),或是 $\mathbb{Z},{\mathbb{Z}}_{+}$ (时间离散系统). 进一步, 对任意 $x\in M$ ,我们要求

**a) ${\phi \ast \ast }^0\left(x\right)=x$ 并且

b) 对任意 $t,s$ ,有 ${\phi }^t\left({\phi }^s\left(x\right)\right)={\phi }^{t+s}\left(x\right)$ . 映射 ${\phi }^1$ 简记为 $\phi$ .

以后,时间集合记为 $\mathrm{\Gamma }$ ,那么 $\mathrm{\Gamma }=\mathbb{R},\mathrm{\Gamma }={\mathbb{R}}_{+},\mathrm{\Gamma }=\mathbb{Z}$ ,或者 $\mathrm{\Gamma }={\mathbb{Z}}_{+}$ . 若 $\mathrm{\Gamma }=\mathbb{R}$ , 则该动力系统也称为流; 若 $\mathrm{\Gamma }=\mathbb{Z}$ 或 $\mathrm{\Gamma }={\mathbb{Z}}_{+}$ ,则动力系统是离散的. 在 $\mathrm{\Gamma }=\mathbb{R}$ 或 $\mathrm{\Gamma }=\mathbb{Z}$ 的情况下,因为对任意 $t\in \mathrm{\Gamma }$ ,性质 a) 和性质 b) 成立,所以逆映射 ${\left({\phi }^t\right)}^{-1}={\phi }^{-t}$ 也存在,该动力系统称为可逆动力系统.

如果动力系统不可逆,那么对任意集合 $A\subset M$ 和任意 $t>0,{\phi }^{-t}\left(A\right)$ 表示集合 $A$ 在映射 ${\phi }^t$ 下的原像,即 ${\phi }^{-t}\left(A\right)=\left\{x\in M:{\phi }^t\left(x\right)\in A\right\}$ . 若对任意 $t\in \mathrm{\Gamma }\left(M\subset {\mathbb{R}}^n\right)$ ,映射 ${\phi }^t:M\to M$ 连续或 $k$ 阶连续可微,则称动力系统分别是连续的或是 $C^k$ 光滑的.

给定 $x\in M$ ,映射 $t\to {\phi }^t\left(x\right)$ 定义了动力系统中的一个运动,该运动当 $t=0$ 时, 初始值是 $x$ . 以 $x$ 为初始值的运动的像 $\gamma \left(x\right)$ 称为 $x$ 的轨道,即 $\gamma \left(x\right)=\left\{{\phi }^t\left(x\right)\right\}t\in \mathrm{\Gamma }$ . 类似地,定义 ${\gamma }^{+}\left(x\right)={\left\{{\phi }^t\left(x\right)\right\}}_{t\ge 0}$ 为 $x$ 的正半轨. 若 $\mathrm{\Gamma }\ne {\mathbb{R}}_{+}$ 或 $\mathrm{\Gamma }\ne {\mathbb{Z}}_{+}$ ,则定义 ${\gamma }^{-}\left(x\right)={\left\{{\phi }^t\left(x\right)\right\}}_{t\le 0}$ 为 $x$ 的负半轨.

若 $\gamma \left(x\right)=\{x\}$ ,则称轨道 $\gamma \left(x\right)$ 是稳态的(平衡点,不动点). 若存在 $T\in \mathrm{\Gamma },T>$ 0,使得对任意 $t\in \mathrm{\Gamma }$ ,有 ${\phi }^{t+T}\left(x\right)={\phi }^t\left(x\right)$ 并且 $T\in \mathrm{\Gamma }$ 是满足上述性质的最小整数,则称轨道 $\gamma \left(x\right)$ 是 $T$ 周期的. 常数 $T$ 称为周期.

2. 微分方程的流

考虑微分方程

$$\begin{array}{}\text{(17.1)}& \dot{x}=f\left(x\right),\end{array}$$

其中, $f:M\to {\mathbb{R}}^n$ (向量场) 是 $r$ 阶连续可微的, $M={\mathbb{R}}^n$ 或者 $M$ 是 ${\mathbb{R}}^n$ 中的开子集. 以后,在 ${\mathbb{R}}^n$ 中采用欧几里得范数,即对任意 $x\in {\mathbb{R}}^n,x=\left(x_1,\cdots ,x_n\right)$ ,模 $\parallel x\parallel =\sqrt{\sum _{i=1}^n{x}_i^2}$ . 如果将映射 $f$ 写成分量形式 $f=\left(f_1,\cdots ,f_n\right)$ ,则 (17.1) 是由 $n$ 个标量微分方程 ${\dot{x}}_i=f_i\left(x_1,\cdots ,x_n\right),i=1,2,\cdots ,n$ 构成的方程组.

根据微分方程解的存在唯一性定理 (皮卡-林德勒夫定理) 和解对初值的 $r$ 阶可微性定理,我们有对任意 $x_0\in M$ ,存在常数 $\epsilon >0$ ,球面 $B_{\delta }\left(x_0\right)=\{x:\Vert \begin{array}{c}x-x_0\end{array}\Vert <$ $\delta \}\subset M$ 和映射 $\phi :\left(-\epsilon ,\epsilon \right)\times B_{\delta }\left(x_0\right)\to M$ ,使得

(1) $\phi \left(\cdot ,\cdot \right)$ 关于第一个变量 (时间) 是 $r+1$ 阶连续可微的,关于第二个变量 (相变量) 是 $r$ 阶连续可微的;

(2) 给定 $x\in B_{\delta }\left(x_0\right),\phi \left(\cdot ,x\right)$ 是方程 (17.1) 在时间区间 $\left(-\epsilon ,\epsilon \right)$ 上,满足当 $t=0$ 时,初始值为 $x$ 的局部唯一解,也就是说,对任意 $t\in \left(-\epsilon ,\epsilon \right)$ ,有 $\frac{\partial \phi }{\partial t}\left(t,x\right)=$ $\dot{\phi }\left(t,x\right)=f\left(\phi \left(t,x\right)\right),\phi \left(0,x\right)=x$ ,并且任意一个当 $t=0$ 时,初始值为 $x$ 的解在 $\left|t\right|$ 很小范围内与 $\phi \left(t,x\right)$ 重合.

假设方程 (17.1) 的每个局部解均可唯一延拓至整个 $\mathbb{R}$ . 那么存在一个映射 $\phi$ : $\mathbb{R}\times M\to M$ 满足下面的性质:

(1) 对任意 $x\in M$ ,有 $\phi \left(0,x\right)=x$ .

(2) 对任意 $t,s\in \mathbb{R},x\in M$ ,有 $\phi \left(t+s,x\right)=\phi \left(t,\phi \left(s,x\right)\right)$ .

(3) $\phi \left(\cdot ,\cdot \right)$ 关于第一个变量是 $r+1$ 阶连续可微的,关于第二个变量是 $r$ 阶连续可微的.

(4) 给定 $x\in M,\phi \left(\cdot ,x\right)$ 是方程 (17.1) 在整个实数 $\mathbb{R}$ 上的一个解.

从而,定义 ${\phi }^t\text{:=}\phi \left(t,\cdot \right)$ 是由方程 (17.1) 诱导出的 $C^r$ 光滑流. 方程 (17.1) 中流的运动 $\phi \left(\cdot ,x\right):\mathbb{R}\to M$ 称为积分曲线.

口方程

$$\begin{array}{}\text{(17.2)}& \dot{x}=\sigma \left(y-x\right),\dot{y}=rx-y-xz,\dot{z}=xy-bz\end{array}$$

称为对流湍流的洛伦茨 (Lorenz) 系统(参见第 1153 页 17.2.4.3). 其中,参数 $\sigma >$ $0,r>0,b>0.M={\mathbb{R}}^3$ 上的 $C^{\mathrm{\infty }}$ 流对应于洛伦茨系统.

3. 离散动力系统

考虑差分方程

$$\begin{array}{}\text{(17.3)}& x_{t+1}=\phi \left(x_t\right),\end{array}$$

也可记为 $x\to \phi \left(x\right)$ . 其中, $\phi :M\to M$ 是连续映射,或者当 $M\subset {\mathbb{R}}^n$ 时, $\phi :M\to$ $M$ 是 $r$ 阶连续可微映射. 若 $\phi$ 可逆,则通过 $\phi$ 的迭代,方程 (17.3) 可定义可逆离散动力系统. 具体地说,

$$\text{当}t>0\text{时,}{\phi }^t=\underset{t\text{次}}{\underbrace{\phi \circ \cdots \circ \phi }}\text{,}$$$$\begin{array}{}\text{(17.4)}& \text{当}t<0\text{时,}{\phi }^t=\underset{-t\text{次 }}{\underbrace{{\phi }^{-1}\circ \cdots \circ {\phi }^{-1}}},{\phi }^0=id\text{.}\end{array}$$

若 $\phi$ 不可逆,则仅当 $t\ge 0$ 时,可定义映射 ${\phi }^t$ .

$◼\mathbf{A}$: 差分方程

$$\begin{array}{}\text{(17.5)}& x_{t+1}=\alpha x_t\left(1-x_t\right),t=0,1,\cdots \end{array}$$

称为逻辑斯谛(logistic) 方程,其中参数 $\alpha \in (0,4]$ . 这里, $M=\left[0,1\right]$ ,并且对给定的 $\alpha ,\phi :\left[0,1\right]\to \left[0,1\right]$ 定义为 $\phi \left(x\right)=\alpha x\left(1-x\right)$ . 显然, $\phi$ 是无穷阶可微的,但是不可逆. 因此, 方程 (17.5) 定义了一个不可逆动力系统.

$◼\mathbf{B}$: 差分方程

$$\begin{array}{}\text{(17.6)}& x_{t+1}=y_t+1-a{x}_t^2,y_{t+1}=b{x}_t,t=0,\pm 1,\cdots ,\end{array}$$

称为埃农(Hénon) 映射,其中参数 $a>0,b\ne 0$ . 在方程 (17.6) 中,映射 $\phi :{\mathbb{R}}^2\to {\mathbb{R}}^2$ 定义为 $\phi \left(x,y\right)=\left(y+1-a{x}^2,bx\right)$ . 该映射无穷阶可微并且可逆.

4. 积收缩系统和保体积系统

$M\subset {\mathbb{R}}^n$ 上的可逆动力系统 ${\left\{{\phi }^t\right\}}_{t\in \mathrm{\Gamma }}$ 称为体积收缩或耗散的(保体积或保守的),如果对任意具有正 $n$ 维体积 $\mathrm{vol}\left(A\right)$ 的集合 $A\subset M$ ,任意 $t>0\left(t\in \mathrm{\Gamma }\right)$ ,有$\mathrm{vol}\left({\phi }^t\left(A\right)\right)<\mathrm{val}\left(A\right)\left(\mathrm{vol}\left({\phi }^t\left(A\right)\right)=\mathrm{val}\left(A\right)\right).$

$◼\mathbf{A}$: 在方程 (17.3) 中,设 $\phi$ 是 $C^r$ 微分同胚(即 $\phi :M\to M$ 可逆, $M\subset {\mathbb{R}}^n$ 是开集, $\phi$ 和 ${\phi }^{-1}$ 是 $C^r$ 光滑). 令 $D\phi \left(x\right)$ 是 $\phi$ 在 $x\in M$ 处的雅可比矩阵. 若对任意 $x\in M,\left|detD\phi \left(x\right)\right|<1$ ,则离散系统 (17.3) 是耗散系统. 若在 $M$ 中 $\left|detD\phi \left(x\right)\right|\equiv 1$ ,则离散系统 (17.3) 是保守系统.

$◼\mathbf{B}$: 对于系统 (17.6), $D\phi \left(x,y\right)=\left(\begin{array}{cc}-2ax& 1\\ b& 0\end{array}\right)$ ,于是 $\left|detD\phi \left(x,y\right)\right|\equiv b$ . 因此, 若 $\left|b\right|<1$ ,系统 (17.6) 是耗散系统; 若 $\left|b\right|=1$ ,系统 (17.6) 是保守系统.

埃农映射可以分解成三个映射 (图 17.1): 首先,保面积映射 $x^{\prime }=x,y^{\prime }=y+$ $1-a{x}^2$ 将初始区域伸展和弯曲; 然后,映射 $x^{\prime \prime }=b{x}^{\prime },y^{\prime \prime }=y^{\prime }$ 将区域沿 $x^{\prime }$ 轴压缩 (当 $\left|b\right|<1$ ); 最后,映射 $x^{\prime \prime \prime }=y^{\prime \prime },y^{\prime \prime \prime }=x^{\prime \prime }$ 将区域以直线 $y^{\prime \prime }=x^{\prime \prime }$ 为轴作反射.

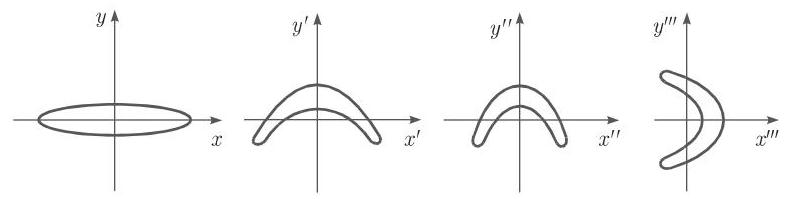
17.1.1.2 不变集

1. $\alpha$ 极限集、 $\omega$ 极限集、吸收集

令 ${\left\{{\phi }^t\right\}}_{t\in \mathrm{\Gamma }}$ 是 $M$ 上的动力系统. 若集合 $A\subset M$ 满足对任意 $t\in \mathrm{\Gamma }$ ,有 ${\phi }^t\left(A\right)=A$ ,则称 $A$ 是 $\left\{{\phi }^t\right\}$ 的不变集. 若集合 $A\subset M$ 满足对任意 $t\ge 0,t\in \mathrm{\Gamma }$ , 有 ${\phi }^t\left(A\right)\subset A$ ,则称 $A$ 是 $\left\{{\phi }^t\right\}$ 的正向不变集. 对任意 $x\in M,x$ 的轨道的 $\omega$ 极限集定义为下面的集合:

$$\begin{array}{}\text{(17.7)}& \omega \left(x\right)=\left\{y\in M:\mathrm{\exists }{t}_n\in \mathrm{\Gamma },t_n\to +\mathrm{\infty },{\phi }^{t_n}\left(x\right)\to y\text{ 当 }n\to +\mathrm{\infty }\right\}.\end{array}$$

$\omega \left(x\right)$ 中的点称为轨道的 $\omega$ 极限点. 若动力系统是可逆的,则对任意 $x\in M$ ,集合

$$\begin{array}{}\text{(17.8)}& \alpha \left(x\right)=\left\{y\in M:\mathrm{\exists }{t}_n\in \mathrm{\Gamma },t_n\to -\mathrm{\infty },{\phi }^{t_n}\left(x\right)\to y\text{ 当 }n\to +\mathrm{\infty }\right\}\end{array}$$

称为 $x$ 的轨道的 $\alpha$ 极限集; $\alpha \left(x\right)$ 中的点称为轨道的 $\alpha$ 极限点.

对于体积收缩的动力系统, 在相平面上存在一个有界集合使得随着时间的推移, 到达此集合的条轨道将留在这个集合内. 一个有界连通开集 $U\subset M$ 称为 ${\left\{{\phi }^t\right\}}_{t\in \mathrm{\Gamma }}$ 的吸收集,如果对任意 $t>0,t\in \mathrm{\Gamma }$ ,有 ${\phi }^t\left(\overline{U}\right)\subset U.(\overline{U}$ 表示 $U$ 的闭包. $)$

• 考虑平面微分方程

$$\begin{array}{}\text{(17.9a)}& \dot{x}=-y+x\left(1-x^2-y^2\right),\dot{y}=x+y\left(1-x^2-y^2\right)\end{array}$$

根据极坐标变换 $x=r\cos \theta ,y=r\sin \theta$ ,方程 (17.9a) 满足当 $t=0$ 时,初始状态为 $\left(r_0,v_0\right)$ 的解具有下面的形式:

$$\begin{array}{}\text{(17.9b)}& r\left(t,r_0\right)={[1+(r_0^{-2}-1){\mathrm{e}}^{-2t}]}^{-1/2},v\left(t,v_0\right)=t+v_0.\end{array}$$

上述解的形式表明方程 (17.9a) 的流中存在周期为 $2\pi$ 的周期轨,它可表示为 $\gamma$ $\left(\left(1,0\right)\right)=\{\left(\cos t,\sin t\right),t\in \left[0,2\pi \right]\}$ . 点 $p$ 的轨道的极限集是

$$\alpha \left(p\right)=\{\begin{array}{ll}\left(0,0\right),& \parallel p\parallel <1,\\ \gamma \left(\left(1,0\right)\right),& \parallel p\parallel =1,\\ \varnothing ,& \parallel p\parallel >1\end{array}\text{ 和 }\omega \left(p\right)=\{\begin{array}{ll}\gamma \left(\left(1,0\right)\right),& p\ne \left(0,0\right),\\ \left(0,0\right),& p=\left(0,0\right).\end{array}$$

对于系统 (17.9a),给定 $r>1$ ,任意开集 $B_r=\left\{\left(x,y\right):x^2+y^2<r^2\right\}$ 是吸收集.

2. 不变集的稳定性

设 $A$ 是空间 $\left(M,\rho \right)$ 上动力系统 ${\left\{{\phi }^t\right\}}_{t\in \mathrm{\Gamma }}$ 的一个不变集. 若对 $A$ 的任意邻域 $U$ ,存在 $A$ 的另一个邻域 $U_1\subset U$ ,使得对任意 $t>0$ ,有 ${\phi }^t\left(U_1\right)\subset U$ ,则称 $A$ 是稳定的. 设 $A$ 是 $\left\{{\phi }^t\right\}$ 的不变集,若 $A$ 是稳定的并且满足

$$\begin{array}{}\text{(17.10)}& \mathrm{\exists }\mathrm{\Delta }>0,\begin{array}{l}\mathrm{\forall }x\in M\\ \mathrm{dist}\left(x,A\right)<\mathrm{\Delta }\end{array}\}:\text{ 当 }t\to +\mathrm{\infty }\text{,有 }\mathrm{dist}\left({\phi }^t\left(x\right),A\right)\to 0,\end{array}$$

其中, $\mathrm{dist}\left(x,A\right)=\underset{y\in A}{inf}\rho \left(x,y\right)$ ,则称 $A$ 是渐近稳定的.

3. 紧致集

设 $\left(M,\rho \right)$ 是度量空间. 一族开集 ${\left\{U_i\right\}}_{i\in I}$ 称为 $M$ 的开覆盖,如果 $M$ 中对任意一点都至少属于某个 $U_i$ . 度量空间 $\left(M,\rho \right)$ 称为紧致的,如果任意 $M$ 的开覆盖 ${\left\{U_i\right\}}_{i\in I}$ 都存在有限多个集合 $U_{i_1},\cdots ,U_{i_r}$ 使得 $M=U_{i_1}\cup \cdots \cup U_{i_r}$ . 集合 $K\subset M$ 称为紧致的,如果 $K$ 作为子空间是紧致的.

4. 吸引子、吸引域

设 ${\left\{{\phi }^t\right\}}_{t\in \mathrm{\Gamma }}$ 是 $\left(M,\rho \right)$ 上的动力系统, $A$ 是 $\left\{{\phi }^t\right\}$ 的不变集. 那么, $W\left(A\right)=\{x\in$ $M:\omega \left(x\right)\subset A\}$ 称为 $A$ 的吸引域. 紧致集 $\mathrm{\Lambda }\subset M$ 称为 $M$ 上动力系统 ${\left\{{\phi }^t\right\}}_{t\in \mathrm{\Gamma }}$ 的吸引子,如果 $\mathrm{\Lambda }$ 是 $\left\{{\phi }^t\right\}$ 的不变集,并且存在 $\mathrm{\Lambda }$ 的开邻域 $U$ ,使得对几乎处处的 (勒贝格测度意义下 $)x\in U$ ,有 $\omega \left(x\right)=\mathrm{\Lambda }$ .

$◼\mathrm{\Lambda }=\gamma \left(\left(1,0\right)\right)$ 是方程(17.9a)中流的一个吸引子. 其中, $W\left(\mathrm{\Lambda }\right)={\mathbb{R}}^2\setminus \{\left(0,0\right)\}$ . 在某些动力系统中,吸引子有更广泛的含义. 存在这样的不变集 $\mathrm{\Lambda }$ ,它的任意邻域都含有周期轨,这些周期轨没有被 $\mathrm{\Lambda }$ 吸引,例如费根鲍姆 (Feigenbaum) 吸引子. 集合 $\mathrm{\Lambda }$ 可能不仅由单个 $\omega$ 极限集组成. 紧致集合 $\mathrm{\Lambda }$ 称为 $M$ 上动力系统 ${\left\{{\phi }^t\right\}}_{t\in \mathrm{\Gamma }}$ 的米尔诺(Milnor) 吸引子,如果 $\mathrm{\Lambda }$ 是 $\left\{{\phi }^t\right\}$ 的不变集,并且 $\mathrm{\Lambda }$ 的吸引域包含一个正的勒贝格测度集.