5.3.7 环和域

这一节讨论具有两个二元运算的代数结构.

5.3.7.1 定义

1. 环

具有两个二元运算 + 和 $\ast$ 的集合 $R$ 称为环(记作 $\left(R,+,\ast \right)$ ),如果

• $\left(R,+\right)$ 是一个阿贝尔群;

• $\left(R,\ast \right)$ 是一个半群;

• 分配律成立:

$$\begin{array}{}\text{(5.173)}& a\ast \left(b+c\right)=\left(a\ast b\right)+\left(a\ast c\right),\left(b+c\right)\ast a=\left(b\ast a\right)+\left(c\ast a\right).\end{array}$$

如果 $\left(R,\ast \right)$ 是交换的或者 $\left(R,\ast \right)$ 有中性元素,那么 $\left(R,+,\ast \right)$ 分别称作交换环或有恒等元素环 (有单位元素环).

有单位元素并且没有零因子的交换环称作整区.

环的非零元称为零因子或奇异元素, 如果存在环的非零元使得它们的积等于零.

在有零因子的环中下列的蕴涵关系一般是错误的: $a\ast b=0\Rightarrow \left(a=0\vee b=0\right)$ .

如果 $R$ 是有单位元素环,那么最小的使得 $k1=1+1+\cdots +1=0(k$ 乘 1 等于零) 的自然数 $k$ 称为环 $R$ 的特征,并记为 $\mathrm{char}R=k$ . 如果这样的 $k$ 不存在,那么 $\mathrm{char}R=0$ .

$\mathrm{char}R=k$ 意味着加群 $\left(R,+\right)$ 的由 1 生成的循环子群 $⟨1⟩$ 有阶 $k$ ,因而每个元素的阶都是 $k$ 的因子.

如果 $\mathrm{char}R=k$ ,那么对于所有 $r\in R,r+r+\cdots +r\left(k\right)$ 次) 等于零. 整区的特征是零或素数.

2. 除环、域

如果 $\left(R\setminus \{0\},\ast \right)$ 是一个群,那么环 $R$ 称为除环或斜域. 如果 $\left(R\setminus \{0\},\ast \right)$ 是交换群,那么 $R$ 是一个域. 因此,每个域是一个整区,并且也是一个除环. 反之,每个有限整区以及每个有限除环是一个域. 这个命题称作韦德伯恩 (Wedderburn) 定理.

环和域的例子

$◼\mathbf{A}$ : 数集 $\mathbb{Z},\mathbb{Q},\mathbb{R}$ 和 $\mathbb{C}$ 对于加法和乘法是有恒等元环; $\mathbb{Q},\mathbb{R}$ 和 $\mathbb{C}$ 也是域. 偶数集是没有恒等元的环的例子.

$◼\mathbf{B}$ : 所有 $n$ 阶实 (或复) 元素方阵的集合 $M_n$ 对于矩阵加法和乘法是一个非交换环. 它有单位元,即恒等矩阵. $M_n$ 有零因子,例如,当 $n=2$ 时, $\left(\begin{array}{ll}1& 0\\ 1& 0\end{array}\right)\left(\begin{array}{ll}0& 0\\ 1& 1\end{array}\right)$ $=\left(\begin{array}{ll}0& 0\\ 0& 0\end{array}\right)$ ,即矩阵 $\left(\begin{array}{ll}1& 0\\ 1& 0\end{array}\right)$ 和 $\left(\begin{array}{ll}0& 0\\ 1& 1\end{array}\right)$ 是 $M_n$ 中的零因子.

$◼\mathbf{C}$: 实多项式 $p\left(x\right)=a_n{x}^n+a_{n-1}{x}^{n-1}+\cdots +a_{1}x+a_0$ 的集合对于多项式的通常加法和乘法形成一个环,即多项式环 $\mathbb{R}\left[x\right]$ . 更一般些,代替 $\mathbb{R}$ 上的多项式,可以考虑任意有恒等元的交换环上的多项式环.

$◼\mathbf{D}$: 模 $n$ 剩余类环 ${\mathbb{Z}}_n$ 是有限环的例子. ${\mathbb{Z}}_n$ 由所有除以 $n$ 时有相同余数的整数的类 ${\left[a\right]}_n$ 组成 $({\left[a\right]}_n$ 是在 447 页 5.2.4,1. 引进的由自然数 $a$ 对于关系 ${\sim }_R$ 定义的等价类). ${\mathbb{Z}}_n$ 上的环运算 $\oplus ,\odot$ 定义为

$$\begin{array}{}\text{(5.174)}& {\left[a\right]}_n\oplus {\left[b\right]}_n={[a+b]}_n\text{ 和 }{\left[a\right]}_n\odot {\left[b\right]}_n={[a\cdot b]}_n.\end{array}$$

如果自然数 $n$ 是素数,那么 $\left({\mathbb{Z}}_n,\oplus ,\odot \right)$ 是一个域. 不然 ${\mathbb{Z}}_n$ 有零因子,例如,在 ${\mathbb{Z}}_6$ 中 ${\left[3\right]}_6\cdot {\left[2\right]}_6={\left[0\right]}_6$ . 通常 ${\mathbb{Z}}_n$ 看作 ${\mathbb{Z}}_n=\{0,1,\cdots ,n-1\}$ ,即用代表元 (参见第 505 页 $5.4.3,3.)$ 代替剩余类.

3. 域扩张

设 $K$ 和 $L$ 是域,并且 $K\subseteq L$ ,那么 $L$ 是 $K$ 的扩域或扩张域. 此时 $L$ 可看作 $K$ 上的向量空间.

如果 $L$ 是 $K$ 上的有限维空间,那么 $L$ 称为一个有限扩域. 如果这个维数是 $n$ , 那么 $L$ 也称为 $K$ 的 $n$ 次扩张(记号: $\left[L:K\right]=n$ ).

例如, $\mathbb{C}$ 是 $\mathbb{R}$ 的有限扩张. $\mathbb{C}$ 在 $\mathbb{R}$ 上是 2 维的,并且 $\{1,\mathrm{i}\}$ 是基. $\mathbb{R}$ 是 $\mathbb{Q}$ 上的无限维空间.

对于集合 $M\subseteq L,K\left(M\right)$ 表示含有域 $K$ 及集合 $M$ 的最小的域 $(K$ 的一个扩域).

特别重要的是单代数扩张 $K\left(\alpha \right)$ ,这里 $\alpha \in L$ 是 $K\left[x\right]$ 中一个多项式的根. 以 $\alpha$ 为根的最低次数并且首项系数为 1 的多项式称为 $\alpha$ 在 $K$ 上的极小多项式. 如果 $\alpha \in L$ 的极小多项式的次数是 $n$ ,那么 $K\left(\alpha \right)$ 是 $n$ 次扩张,即极小多项式的次数等于 $L$ 作为 $K$ 上向量空间的维数.

例如, $\mathbb{C}=\mathbb{R}\left(\mathrm{i}\right)$ ,并且 $\mathrm{i}\in \mathbb{C}$ 是多项式 $x^2+1\in \mathbb{R}\left[x\right]$ 的根,即 $\mathbb{C}$ 是单代数扩张, 并且 $\left[\mathbb{C}:\mathbb{R}\right]=2$ .

没有任何真子域的域称作素域.

每个域 $k$ 都含有一个最小的子域,即 $K$ 的素域.

除同构外, $\mathbb{Q}$ (对于特征 0 的域),以及 ${\mathbb{Z}}_p\left(p\text{是素数}\right)$ (对于特征 $p$ 的域) 是单素域.

5.3.7.2 子环、理想

1. 子环

设 $R=\left(R,+,\ast \right)$ 是一个环,以及 $U\subseteq R$ . 如果 $U$ 对于+和 $\ast$ 也是一个环,那么 $U=\left(U,+,\ast \right)$ 称作 $R$ 的子环.

环 $\left(R,+,\ast \right)$ 的非空子集 $U$ 形成 $R$ 的子环,当且仅当对于所有 $a,b\in U,a+\left(-b\right)$ 和 $a\ast b$ 也在 $R$ 中 (子环判别法).

2. 理想

子环 $I$ 称为理想,如果对于所有 $a\in I$ 和 $a\in R,r\ast a$ 和 $a\ast r$ 也在 $I$ 中. 这些特殊的子环是形成商环的基础 (参见第 486 页 5.3.7.3).

平凡子环 $\{0\}$ 和 $R$ 总是 $R$ 的理想. 域只有平凡子环.

3. 主理想

如果一个理想的所有元素可以由一个元素依据子环判别法生成, 那么它称为主理想. $\mathbb{Z}$ 的所有理想都是主理想. 它们可以写作 $m\mathbb{Z}=\{mg\mid g\in \mathbb{Z}\}$ 的形式,并且将它们记作(m).

5.3.7.3 同态、同构、同态定理

1. 环同态和环同构

(1) 环同态 设 $R_1=\left(R_1,+,\ast \right)$ 和 $R_2=\left(R_2,{\circ }_{+},{\circ }_{\ast }\right)$ 是两个环. 映射 $h$ : $R_1\to R_2$ 称为环同态,如果对于所有 $a,b\in R_1$ ,

$$\begin{array}{}\text{(5.175)}& h\left(a+b\right)=h\left(a\right){\circ }_{+}h\left(b\right)\text{ 及 }h\left(a\ast b\right)=h\left(a\right){\circ }_{\ast }h\left(b\right)\end{array}$$

成立.

(2) 核 $h$ 的核是 $R_1$ 的在 $h$ 作用下的象是 $\left(R_2,+\right)$ 的中性元素 0 的那些元素的集合,并且记作 $\ker h$ :

$$\begin{array}{}\text{(5.176)}& \ker h=\left\{a\in R_1\mid h\left(a\right)=0\right\}.\end{array}$$

这里 $\ker h$ 是 $R_1$ 的一个理想.

(3) 环同构 如果 $h$ 还是双射,那么 $h$ 称为环同构,并且称环 $R_1$ 和 $R_2$ 是同构的.

(4) 商环 如果 $I$ 是环 $\left(R,+,\ast \right)$ 的理想,那么 $I$ 在环 $R$ 的加群 $\left(R,+\right)$ 中的陪集 $\{a+I\mid a\in R\}$ (参见第 452 页 5.3.3,1.) 的集合对于运算

$$\begin{array}{}\text{(5.177)}& \left(a+I\right){\circ }_{+}\left(b+I\right)=\left(a+b\right)+I\text{ 和 }\left(a+I\right){\circ }_{\ast }\left(b+I\right)=\left(a\ast b\right)+I\end{array}$$

形成一个环. 这个环称为 $R$ 对于 $I$ 的商环,并将它记作 $R/I$ .

$\mathbb{Z}$ 对于主理想(m)的商环是剩余类环 ${\mathbb{Z}}_m=Z/\left(m\right)$ (参见第 484 页的环和域的例子).

2. 环同态定理

如果在群同态定理中用理想的概念代替正规子群的概念, 那么就可得到环同态定理: 环同态 $h:R_1\to R_2$ 定义 $R_1$ 的一个理想,即 $\ker h=\left\{a\in R_1\mid h\left(a\right)=0\right\}$ . 商环 $R_1/\ker h$ 同构于同态象 $h\left(R_1\right)=\left\{h\left(a\right)\mid a\in R_1\right\}$ . 反之, $R_1$ 的每个理想 $I$ 定义一个同态映射 ${\mathrm{nat}}_I:R_1\to R_2/I$ ,并且 ${\mathrm{nat}}_I\left(a\right)=a+I$ . 映射 ${\mathrm{nat}}_I$ 称为自然同态.

5.3.7.4 有限域与移位寄存器

1. 有限域

下列的论述给出有限域结构的概要.

(1) 伽罗瓦 (Galois) 域 GF 对于每个素数幂 $p^n$ 存在唯一的含 $p^n$ 个元素的域 (不计同构),并且每个有限域有 $p^n$ 个元素. 含 $p^n$ 个元素的域记作 $\mathrm{GF}\left(p^n\right)$ (伽罗瓦域).

注意: 对于 $n>1,\mathrm{GF}\left(p^n\right)$ 与 ${\mathbb{Z}}_{p^n}$ 是不同的.

在构造含 $p^n$ 个元素 $\left(p\text{是素数,}n>1\right)$ 时,需要 ${\mathbb{Z}}_p$ 上的多项式环 (参见第 484 页 5.3.7.1, $2.,◼\mathrm{C})$ 和不可约多项式: ${\mathbb{Z}}_p\left[x\right]$ 由所有的系数属于 ${\mathbb{Z}}_p$ 的多项式组成. 这些系数按模 $p$ 计算.

(2) 带余除法和欧几里得算法 在多项式环 $K\left[x\right]$ 中可以应用带余除法 (带有余数的多项式相除),即对于 $f\left(x\right),g\left(x\right)\in K\left[x\right],\mathrm{deg}f\left(x\right)\le \mathrm{deg}g\left(x\right)$ ,存在 $q\left(x\right),r\left(x\right)\in$ $K\left[x\right]$ ,使得

$$\begin{array}{}\text{(5.178)}& g\left(x\right)=q\left(x\right)\cdot f\left(x\right)+r\left(x\right),\text{ 并且 }\mathrm{deg}r\left(x\right)\le \mathrm{deg}f\left(x\right).\end{array}$$

这个关系式记作 $r\left(x\right)=g\left(x\right)\left(\mathrm{mod}f\left(x\right)\right)$ . 带余除法的重复实施称作多项式环的欧几里得算法,并且最后的非零余数给出 $f\left(x\right)$ 和 $g\left(x\right)$ 的最大公因子.

(3) 不可约多项式 若多项式 $f\left(x\right)\in K\left[x\right]$ 不能表示为较低次数的多项式之积, 即 (类似于 $\mathbb{Z}$ 中的素数) $f\left(x\right)$ 是 $K\left[x\right]$ 中的素元素,则称它是不可约的. 例如,对于二次或三次多项式,不可约性意味着它们在 $K$ 中没有根.

可以证明, $K\left[x\right]$ 中存在任意次数的不可约多项式. 如果 $f\left(x\right)\in K\left[x\right]$ 是不可约多项式, 那么

$$\begin{array}{}\text{(5.179)}& K\left[x\right]/f\left(x\right)\text{:=}\{p\left(x\right)\in K\left[x\right]\mid \mathrm{deg}p\left(x\right)<\mathrm{deg}f\left(x\right)\}\end{array}$$

是一个域,这里加法和乘法由模 $f\left(x\right)$ 实施,即 $g\left(x\right)\ast h\left(x\right)=g\left(x\right)\cdot h\left(x\right)\left(\mathrm{mod}f\left(x\right)\right)$ .

如果 $K={\mathbb{Z}}_p$ ,并且 $\mathrm{deg}f\left(x\right)=n$ ,那么 $K\left[x\right]/f\left(x\right)$ 有 $p^n$ 个元素,即 $\mathrm{GF}\left(p^n\right)=$ ${\mathbb{Z}}_p/f\left(x\right)$ ,其中 $f\left(x\right)$ 是 $n$ 次不可约多项式.

(4) $\mathrm{GF}\left(p^n\right)$ 中的计算法则 在 $\mathrm{GF}\left(p^n\right)$ 中下列有用的法则成立:

$$\begin{array}{}\text{(5.180)}& {(a+b)}^{p^r}=a^{p^r}+b^{p^r},r\in \mathbb{N}.\end{array}$$

于是在 $\mathrm{GF}\left(p^n\right)={\mathbb{Z}}_p/f\left(x\right)$ 中存在一个元素 $\alpha =x$ 是 ${\mathbb{Z}}_p\left(x\right)$ 中不可约多项式 $f\left(x\right)$ 的一个根,并且 $\mathrm{GF}\left(p^n\right)={\mathbb{Z}}_p/f\left(x\right)={\mathbb{Z}}_p\left(\alpha \right)$ . 可以证明 ${\mathbb{Z}}_p\left(\alpha \right)$ 是 $f\left(x\right)$ 的分裂域. ${\mathbb{Z}}_p\left(\alpha \right)$ 中多项式的分裂域是 ${\mathbb{Z}}_p$ 的含 $f\left(x\right)$ 所有根的最小的扩张.

(5) 代数闭包、代数学基本定理 域 $K$ 是代数闭的,如果 $K\left[x\right]$ 中所有多项式的根都在 $K$ 中. 代数学基本定理是说,复数域 $\mathbb{C}$ 是代数闭的. $K$ 的代数扩张 $L$ 称为 $K$ 的代数闭包,如果 $L$ 是代数闭的. 有限域的代数闭包并不有限. 所以存在特征 $p$ 的无限域.

(6) 循环群和乘法群 有限域 $K$ 的乘法群 $K^{\ast }=K\setminus \{0\}$ 是循环的,即存在元素 $a\in K$ 使得 $K^{\ast }$ 的每个元素都是 $a$ 的幂: $K^{\ast }=\left\{1,a,a^2,\cdots ,a^{q-1}\right\}$ (若 $K$ 有 $q$ 个元素).

不可约多项式 $f\left(x\right)\in K\left[x\right]$ 称为本原的,如果 $x$ 的幂表示 $L\text{:=}K\left[x\right]/f\left(x\right)$ 的所有非零元素,即 $L$ 的乘法群 $L^{\ast }$ 可由 $x$ 生成.

应用 $n$ 次本原多项式 $f\left(x\right)$ 有可能从 $\mathrm{GF}\left(p\right)\left[x\right]$ 中构造一个 $\mathrm{GF}\left(p^n\right)$ 的 “对数表”, 这个表使计算简化.

• $\mathrm{GF}\left(2^3\right)$ 的构造和它的对数表.

$f\left(x\right)=1+x+x^3$ 在 $\mathbb{Z}\left[x\right]$ 上不可约,因为无论 0 还是 1 都不是它的根:

$$\begin{array}{}\text{(5.181)}& \mathrm{GF}\left(2^3\right)={\mathbb{Z}}_2\left[x\right]/f\left(x\right)=\left\{a_0+a_{1}x+a_2{x}^2\mid a_0,a_1,a_2\in {\mathbb{Z}}_2\wedge x^3=1+x\right\}.\end{array}$$

$f\left(x\right)$ 是本原的,所以对数表可以从 $\mathrm{GF}\left(2^3\right)$ 中产生.

${\mathbb{Z}}_2\left[x\right]/f\left(x\right)$ 中每个多项式 $a_0+a_{1}x+a_2{x}^2$ 都可以确定两个表达式. 系数向量 $a_0,a_1,a_2$ 和所谓对数,后者乃是使得对于模 $1+x+x^3$ 有 $x^i=a_0+a_{1}x+a_2{x}^2$ 的自然数 $i$ . 对数表是

	KE	KV			Log.
	1	1	0	0	0
	$x$	0	1	0	1
	$x^2$	0	0	1	2
	$x^3$	1	1	0	3
	$x^4$	0	1	1	4
	$x^5$	1	1	1	5
	$x^6$	1	0	1	6

• $\mathrm{GF}\left(8\right)$ 中域元素(KE)的加法:

• 按分量模 2(一般情形模 $p$ ) 坐标向量 (KV) 的加法.

GF(8) 中域元素 (KE) 的乘法:

对数 (Log) 模 7(一般情形模 $\left(p^n-1\right)$ ) 的加法.

例: $\frac{x^2+x^4}{x^3+x^4}=\frac{x}{x^6}=x^{-5}=x^2$ .

注 有限域在编码理论中如线性码是极其重要的,其中考虑 ${\left(\mathrm{GF}\left(q\right)\right)}^n$ 形式的向量空间. 这样的向量空间的子空间称作线性码(参见第 515 页 5.4.6.2,3.). 线性码的元素 (码字) 也是有限域 $\mathrm{GF}\left(q^n\right)$ 的元素形成的 $n$ 组. 应用于码的理论时重要的是要知道 $X^n-1$ 的因子. $X^n-1\in K\left[X\right]$ 的分裂域称为 $K$ 上的第 $n$ 个分圆域. 如果 $K$ 的特征不是 $n$ 的因子,并且 $\alpha$ 是本原 $n$ 次单位根,那么:

a) 扩域 $K\left(\alpha \right)$ 是 $X^n-1$ 在 $K$ 上的分裂域.

b) 在 $K\left(\alpha \right)$ 中, $X^n-1$ 恰有 $n$ 个两两互异的根,它们形成一个循环群,并且其中有 $\phi \left(n\right)$ 个本原 $n$ 次单位根,此处 $\phi \left(n\right)$ 表示欧拉函数 (参见第 509 页 5.4.4,1.). 由一个本原 $n$ 次单位根 $\alpha$ 的 $k$ 次幂 $\left(k<n,gcd\left(k,n\right)=1\right)$ 可得到所有单位根.

2. 移位寄存器的应用

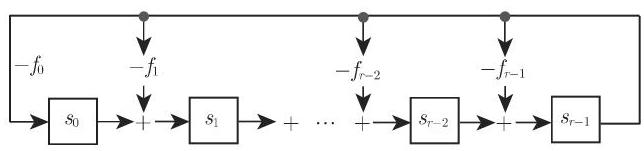
多项式的计算可以由线性反馈移位寄存器 (图 5.18) 很好地实施. 对于基于反馈多项式 $f\left(x\right)=f_0+f_{1}x+\cdots +f_{r-1}{x}^{r-1}+x^r$ 的线性反馈移位寄存器,我们由状态多项式 $s\left(x\right)=s_0+s_{1}x+\cdots +s_{r-1}{x}^{r-1}$ 可得到状态多项式

$$s\left(x\right)\cdot x-s_{r-1}\cdot f\left(x\right)=s\left(x\right)\cdot x\left(\mathrm{mod}f\left(x\right)\right).$$

特别地,如果 $s\left(x\right)=1,i$ 步 (应用 $i$ 次) 后状态多项式是 $x^i\left(\mathrm{mod}f\left(x\right)\right)$ .

对 487 页的例子的证明: 选取本原多项式 $f\left(x\right)=1+x+x^3\in {\mathbb{Z}}_2\left[x\right]$ 作为反馈多项式. 那么长度为 3 的移位寄存器有下列状态序列:

从初始状态开始: $100\widehat{=}1$ $\left(\mathrm{mod}f\left(x\right)\right)$

得到状态如下: $010\widehat{=}x$ $\left(\mathrm{mod}f\left(x\right)\right)$

$001\triangleq x^2$ $\left(\mathrm{mod}f\left(x\right)\right)$

$110\triangleq x^3\equiv 1+x$ $\left(\mathrm{mod}f\left(x\right)\right)$

$011\triangleq x^4\equiv x+x^2$ $\left(\mathrm{mod}f\left(x\right)\right)$

$$111\widehat{=}{x}^5\equiv 1+x+x^2\left(\mathrm{mod}f\left(x\right)\right)$$$$\begin{array}{rlrlr}101& \geqq x^6\equiv 1+x^2& & \left(\mathrm{mod}f\left(x\right)\right)& \\ 100& \geqq x^7& \equiv 1& & \left(\mathrm{mod}f\left(x\right)\right)\end{array}$$

这些状态可以看作状态多项式 $s_0+s_{1}x+s_2{x}^2$ 的系数向量.

一般地: 长度为 $r$ 的线性反馈移位寄存器给出具有极大周期长度 $2^r-1$ 的状态序列,当且仅当反馈多项式是 $r$ 次本原多项式.