16.3.2 描述性统计学

16.3.2.1 对给定数据的统计汇总与分析

为了对某元素的性质进行统计描述,该性质必须用随机变量 $X$ 来刻画. 性质 $X$ 的 $n$ 个测量或观察值 $x_i$ 通常是统计调查的起点,用于探寻 $X$ 的分布的某些参数或 $X$ 的分布本身.

如果试验或测量在相同条件下可重复进行无数次,则每个容量为 $n$ 的测量序列可视为无限总体的随机样本. 测量序列的容量 $n$ 可以很大,统计调查过程如下.

1. 规则、主要记法

测量或观察值 $x_i$ 记录在规则表中.

2. 区间或分组

把样本的 $n$ 个测量数据 $x_i\left(i=1,2,\cdots ,n\right)$ 分到 $k$ 个子区间,即所谓的分组, 或者是长度或宽度为 $h$ 的等组距分组,通常分成 $10\sim 20$ 组.

3. 频率和频率分布

绝对频率 $h_j\left(j=1,2,\cdots ,k\right)$ 指落在给定区间 $\mathrm{\Delta }{x}_j$ 的数据 (占有数) 的个数 $h_j$ . 比值 $h_j/n$ (用 $\mathrm{\%}$ 表示) 称为相对频率. 如果值 $h_j/n$ 用矩形表示分组,则得到给定频率分布的图形表示,也称为直方图(图 16.13(a)). $h_j/n$ 可看作概率或密度函数 $f\left(x\right)$ 的实证数值.

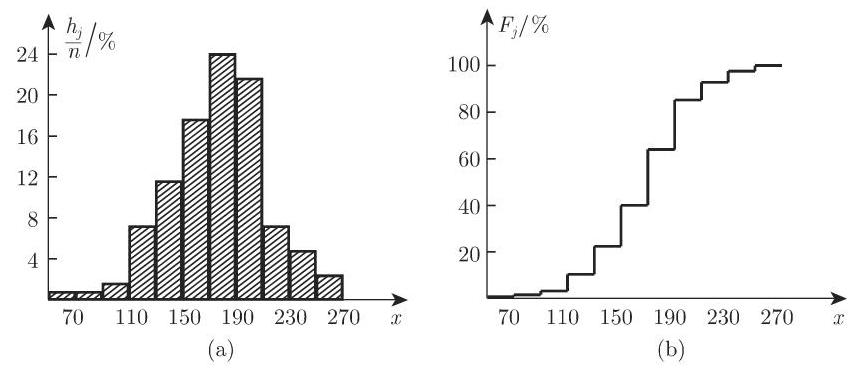
4. 累计频率

把绝对频率或相对频率加起来得到累计绝对频率或累计相对频率

$$\begin{array}{}\text{(16.125)}& F_j=\frac{h_1+h_2+\cdots +h_j}{n}\mathrm{\%}\left(j=1,2,\cdots ,k\right).\end{array}$$

图 16.13(b) 给出了实证分布函数图, 可看作未知基本分布函数的近似.

$◼$ 设某研究进行了 $n=125$ 次测量,结果分散于区间 $\left[50,270\right]$ 内,把区间分组为组数 $k=11$ 、长度 $h=20$ 是合理的. 频率表见表 16.3.

表 16.3 频率表

分组	$h_i$	$\left(h_i/n\right)/\mathrm{\%}$	$F_i/\mathrm{\%}$
50—70	1	0.8	0.8
71—90	1	0.8	1.6
91—110	2	1.6	3.2
111—130	9	7.2	10.4
$131-150$	15	12.0	22.4
151—170	22	17.6	40.0
171—190	30	24.0	64.0
191—210	27	21.6	85.6
211—230	9	7.2	92.8
$231-250$	6	4.8	97.6
251—270	3	2.4	100.0

16.3.2.2 统计参数

在总结和分析了 16.3.2.1 给定的样本数据后, 可推知下述参数是随机变量分布参数的近似值.

1. 均值

直接使用所有的样本测量数据, 样本均值是

$$\begin{array}{}\text{(16.126a)}& \overline{x}=\frac{1}{n}\sum _{i=1}^n{x}_i.\end{array}$$

使用均值 ${\overline{x}}_j$ 和分组频数 $h_j$ ,则

$$\begin{array}{}\text{(16.126b)}& \overline{x}=\frac{1}{n}\sum _{j=1}^k{h}_j{\overline{x}}_j.\end{array}$$

2. 方差

直接使用所有测量数据, 样本方差是

$$\begin{array}{}\text{(16.127a)}& s^2=\frac{1}{n-1}\sum _{i=1}^n{(x_i-\overline{x})}^2.\end{array}$$

使用均值 ${\overline{x}}_j$ 和分组频数 $h_j$ ,则

$$\begin{array}{}\text{(16.127b)}& s^2=\frac{1}{n-1}\sum _{j=1}^k{h}_j{({\overline{x}}_j-\overline{x})}^2.\end{array}$$

组中点 $u_j$ (对应区间的中点) 也经常用来代替 ${\overline{x}}_j$ .

3. 中位数

分布的分位数 $\tilde{x}$ 定义为

$$\begin{array}{}\text{(16.128a)}& P\left(X<\tilde{x}\right)=\frac{1}{2}.\end{array}$$

分位数可能并非唯一确定的点. 样本分位数是

$$\begin{array}{}\text{(16.128b)}& \tilde{x}=\{\begin{array}{ll}{x}_{m+1},& n=2m+1,\\ \frac{x_{m+1}+x_m}{2},& n=2m.\end{array}\end{array}$$

4. 极差

$$\begin{array}{}\text{(16.129)}& R=x_{max}-x_{min}.\end{array}$$

5. 众数或最可能值

它指以最大频率出现的数值,用 $D$ 表示.