2.10.1 定义

面积函数是双曲函数的反函数,即反双曲函数. 函数 $\sinh x,\tanh x$ 和 $\coth x$ 均严格单调,因此没有任何限制地具有唯一反函数; 函数 $\cosh x$ 有两个单调区间, 因此存在两个反函数. 面积一词意指这些函数的几何意义是某些双曲线扇形的面积 (参见第 172 页 3.1.2.2).

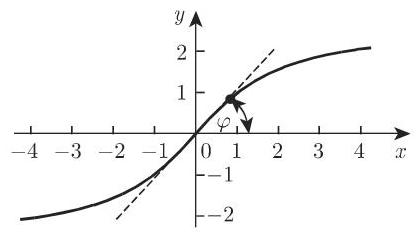
2.10.1.1 面积正弦

函数

$$\begin{array}{}\text{(2.207)}& y=\mathrm{Arsinh}x\end{array}$$

(图 2.53) 为严格单调递增的奇函数, 定义域和值域见表2.8. 该函数等价于表达式 $x=\sinh y$ ,原点为曲线的对称中心和拐点,此处切线的倾斜角 $\phi =\frac{\pi }{4}$ .

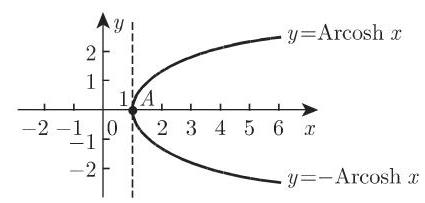
2.10.1.2 面积余弦

函数

$$\begin{array}{}\text{(2.208)}& y=\mathrm{Arcosh}x\text{ 和 }y=-\mathrm{Arcosh}x\end{array}$$

(图 2.54) 或 $x=\cosh y$ 的定义域和值域见表 2.8; 仅当 $x\ge 1$ 时,函数有定义. 函数曲线的起点为 $A\left(1,0\right)$ ,此处有一条垂直切线, $y=\mathrm{Arcosh}x$ 和 $y=-\mathrm{Arcosh}x$ 分别严格单调递增和严格单调递减.

面积函数	定义域	值域	具有相同意义的双曲函数
面积正弦 $y=\mathrm{Arsinh}x$ 面积余弦	$-\mathrm{\infty }<x<\mathrm{\infty }$	$-\mathrm{\infty }<y<\mathrm{\infty }$	$x=\sinh y$
$y=\mathrm{Arcosh}x$		$0\le y<\mathrm{\infty }$
$y=-\mathrm{Arcosh}x$ 面积正切	$1\le x<\mathrm{\infty }$	$-\mathrm{\infty }<y\le 0$	$x=\cosh y$
$y=\mathrm{Artanh}x$ 面积余切	$\left|x\right|<1$	$-\mathrm{\infty }<y<\mathrm{\infty }$	$x=\tanh y$
$y=\mathrm{Arcoth}x$	$\left|x\right|>1$	$-\mathrm{\infty }<y<0$ $0<y<\mathrm{\infty }$	$x=\coth y$

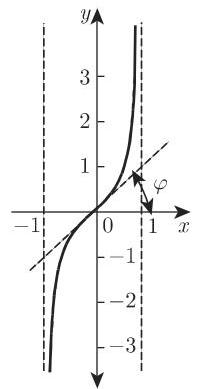
2.10.1.3 面积正切

函数

$$\begin{array}{}\text{(2.209)}& y=\mathrm{Artanh}x\end{array}$$

(图 2.55) 或 $x=\tanh y$ 为奇函数,仅在 $\left|x\right|\le 1$ 时有定义,定义域和值域见表 2.8. 原点为曲线的对称中心和拐点,此处切线的倾斜角 $\phi =\frac{\pi }{4}$ . 函数具有铅直渐近线 $x=\pm 1$ .

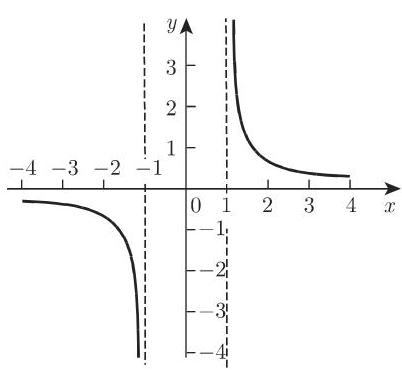
2.10.1.4 面积余切

函数

$$\begin{array}{}\text{(2.210)}& y=\mathrm{Arcoth}x\end{array}$$

(图 2.56) 或 $x=\coth y$ 为奇函数,仅在 $\left|x\right|>1$ 时有定义,定义域和值域见表 2.8. 在区间 $\left(-\mathrm{\infty },-1\right)$ 上,函数从 0 到 $-\mathrm{\infty }$ 严格单调递减,在区间 $\left(1,+\mathrm{\infty }\right)$ 上,函数从 $+\mathrm{\infty }$ 到 0 严格单调递减. 函数有三条渐近线,分别为 $y=0$ 和 $x=\pm 1$ .