Appearance
14.5.3 曲线用复形式的描述
一个实变量
当
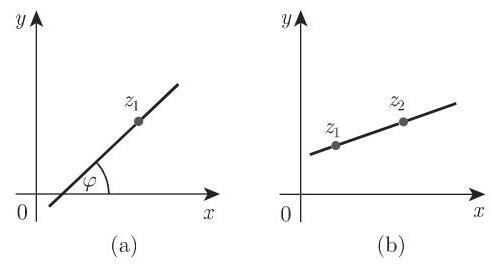
1. 直线
a) 直线,通过一个点
b) 直线,通过两个点
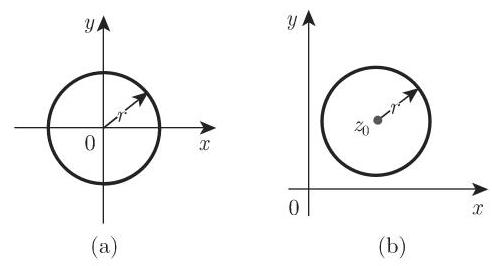
2. 圆周
a) 圆周,半径为
b) 圆周,半径为
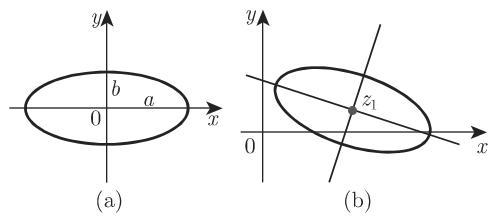
3. 椭圆
a) 椭圆,范式
或
其中
即
b) 椭圆,一般形式 (图 14.51(b)): 中心在
这里
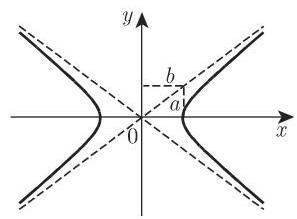
4. 双曲线
双曲线、范式
或
其中
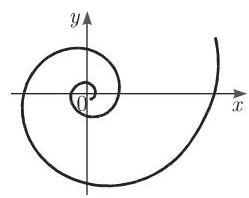
5. 对数螺线 (图 14.53)
其中
Appearance
一个实变量
当
a) 直线,通过一个点
b) 直线,通过两个点
a) 圆周,半径为
b) 圆周,半径为


a) 椭圆,范式
或
其中
即
b) 椭圆,一般形式 (图 14.51(b)): 中心在
这里

双曲线、范式
或
其中
其中

