Appearance
18.2.8 罚函数法和障碍函数法
这些方法的基本原理是通过修正目标函数将约束优化问题转换成一列无约束优化问题. 修正后的问题, 例如, 可以通过 18.2.5 给出的方法求解. 通过适当构造修正的目标函数, 这一修正问题解点列的每个聚点都是原问题的一个解.
18.2.8.1 罚函数法
问题
用如下一列无约束问题代替:
这里
即让可行集
如果
并且序列
例如,如下函数是
或
如果函数
图 18.11 为罚函数方法的示意图.
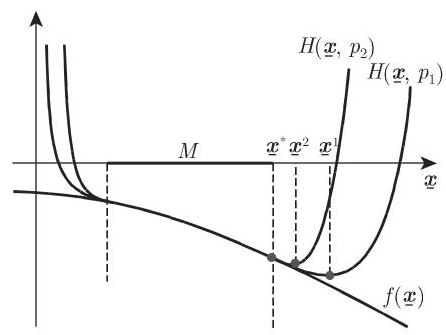
这里
18.2.8.2 障碍函数法
在障碍函数法中, 考虑如下一列修正问题:
这里的项
必须满足,即
并且序列
或
是
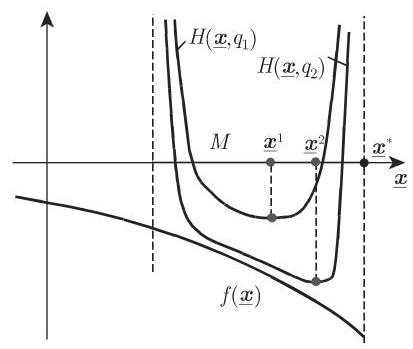
问题 (18.108) 和 (18.113) 第