Appearance
13.2.1 方向导数和空间导数
13.2.1.1 一个标量场的方向导数
一个标量场
如果向量场
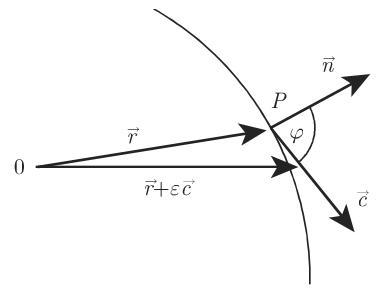
关于单位向量
(13.29)
此后, 方向导数总是指关于一个单位向量的方向导数.
13.2.1.2 一个向量场的方向导数
与标量场的方向导数类似地定义向量场的方向导数. 一个向量场
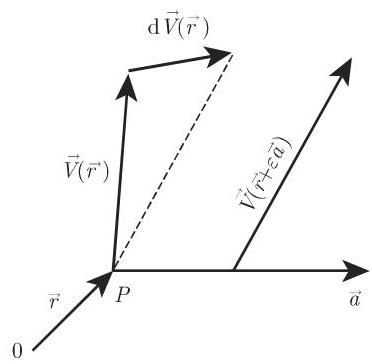
如果向量场
在笛卡儿坐标系中,即对于
在一般坐标系中, 有
(13.32b)
13.2.1.3 体积导数
一个标量场
(1)用一个闭曲面
(2) 在闭曲面上求曲面积分. 这里, 可以考虑以下 3 种类型的积分:
(3) 确定下列极限 (如果它们存在)
这里
(13.33c) 中诸极限被称为体积导数. 从这些导数按给定的次序可以导出一个标量场的梯度 (gradient of a scalar field) 与一个向量场的散度 (divergence) 和旋度 (rotation). 在下一节中, 将详细地讨论这些概念 (甚至重新定义它们).