2.1.3 某些类型的函数

2.1.3.1 单调函数

若对定义域内的任意自变量 $x_1,x_2$ ,当 $x_2>x_1$ 时,函数满足关系

$$\begin{array}{}\text{(2.7a)}& f\left(x_2\right)\ge f\left(x_1\right)\text{ 或 }f\left(x_2\right)\le f\left(x_1\right),\end{array}$$

则称函数为单调递增函数或单调递减函数(图 2.3(a), (b)).

若上述关系 (2.7a) 并非对函数定义域内的每个 $x$ 都成立,而是在其中一个区间或半轴上成立, 则称该函数为此区域内的单调函数. 若函数满足关系

$$\begin{array}{}\text{(2.7b)}& f\left(x_2\right)>f\left(x_1\right)\text{ 或 }f\left(x_2\right)<f\left(x_1\right),\end{array}$$

即 (2.7a) 中的等号恒不成立, 则称函数为严格单调递增函数或严格单调递减函数. 图 2.3(a) 表示一个严格单调递增函数; 图 2.3(b) 表示一个在 $x_1,x_2$ 之间为常数的单调递减函数.

_____ $y={\mathrm{e}}^{-x}$ 是严格单调递减函数, $y=\ln x$ 是严格单调递增函数.

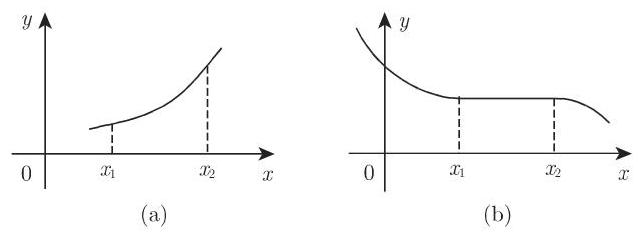
2.1.3.2 有界函数

函数称为有上界函数, 若存在一个数 (称为上界), 使得所有函数值都不超过该数. 函数称为有下界函数, 若存在一个数 (称为下界), 使得所有函数值都不小于该数. 若一个函数既有上界又有下界, 则简称它为有界函数.

A. $y=1-x^2$ 有上界 $\left(y\le 1\right)$ . III $\mathrm{B}:y={\mathrm{e}}^x$ 有下界 $\left(y>0\right)$ .

• $\mathbf{C}:y=\sin x$ 有界 $\left(-1\le y\le +1\right)$ . D. $y=\frac{4}{1+x^2}$ 有界 $\left(0<y\le 4\right)$ .

2.1.3.3 函数的极值

设函数 $f\left(x\right)$ 的定义域为 $D$ ,若对 $\mathrm{\forall }x\in D$ ,有

$$\begin{array}{}\text{(2.8a)}& f\left(a\right)\ge f\left(x\right),\end{array}$$

则称 $f\left(x\right)$ 在点 $a$ 取得绝对极大值或全局极大值. 若不等式 (2.8a) 仅在点 $a$ 的周围,即 $a-\epsilon <x<a+\epsilon ,\epsilon >0,x\in D$ 时成立,则称函数 $f\left(x\right)$ 点 $a$ 取得相对极大值或局部极大值.

类似地, 通过不等式

$$\begin{array}{}\text{(2.8b)}& f\left(a\right)\le f\left(x\right),\end{array}$$

可以定义绝对极小值或全局极小值以及相对极小值或局部极小值.

注 (1) 极大值和极小值也称为极值, 它们与函数的可微性无关, 即定义域内函数不可微的点也可能为极值点. 如曲线的间断点 (参见 75 页图 2.9 和 595 页图 $6.10\left(\mathrm{b}\right),\left(\mathrm{c}\right))$ .

(2) 可微函数中极值的判定准则参见第 595 页 6.1.5.2.

2.1.3.4 偶函数

偶函数(图 2.4(a)) 满足关系

$$\begin{array}{}\text{(2.9a)}& f\left(-x\right)=f\left(x\right).\end{array}$$

若 $f$ 的定义域为 $D$ ,则

$$\begin{array}{}\text{(2.9b)}& \left(x\in D\right)\Rightarrow \left(-x\in D\right).\end{array}$$

2.1.3.5 奇函数

奇函数(图 2.4(b)) 满足关系

$$\begin{array}{}\text{(2.10a)}& f\left(-x\right)=-f\left(x\right).\end{array}$$

若 $f$ 的定义域为 $D$ ,则

$$\begin{array}{}\text{(2.10b)}& \left(x\in D\right)\Rightarrow \left(-x\in D\right).\end{array}$$

$◼\mathbf{A}$: $y=\sin x$ ,

$◼\mathbf{B}$: $y=x^3-x$ .

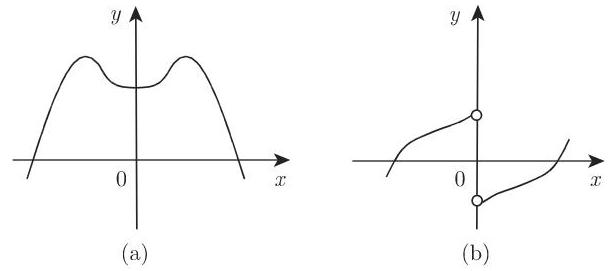
2.1.3.6 偶函数和奇函数的表示

设函数 $f$ 的定义域为 $D$ ,若由 $x\in D$ ,有 $-x\in D$ ,则 $f$ 可写成偶函数 $g$ 与奇函数 $u$ 之和:

$f\left(x\right)=g\left(x\right)+u\left(x\right)$ ,其中 $g\left(x\right)=\frac{1}{2}\left[f\left(x\right)+f\left(-x\right)\right],u\left(x\right)=\frac{1}{2}\left[f\left(x\right)-f\left(-x\right)\right]$ .(2.11)

$f\left(x\right)={\mathrm{e}}^x=\frac{1}{2}\left({\mathrm{e}}^x+{\mathrm{e}}^{-x}\right)+\frac{1}{2}\left({\mathrm{e}}^x-{\mathrm{e}}^{-x}\right)=\cosh x+\sinh x$ (参见第 115 页2.9.1).

2.1.3.7 周期函数

周期函数满足关系

$$\begin{array}{}\text{(2.12)}& f\left(x+T\right)=f\left(x\right),T\text{为非零常数.}\end{array}$$

显然,若上式对于某一常数 $T$ 成立,则对 $T$ 的倍数也成立,满足如上关系的最小正整数称为周期(图 2.5).

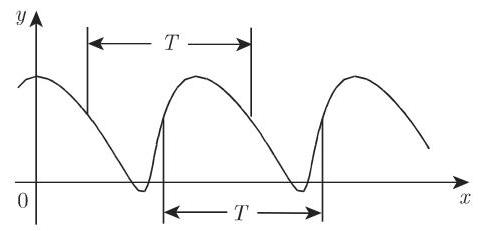
2.1.3.8 反函数

设函数 $y=f\left(x\right)$ 的定义域和值域分别为 $D$ 和 $W$ ,则对于任一 $x\in D$ ,存在唯一的 $y\in W$ . 反之,若对任一 $y\in W$ ,存在唯一的 $x\in D$ ,则可以定义 $f$ 的反函数, 记为 $\phi$ 或 $f^{-1}$ . 其中 $f^{-1}$ 是一个函数符号,并不是 $f$ 的幂.

为求 $f$ 的反函数,交换公式 $f$ 中 $x,y$ 的位置,再利用 $x=f\left(y\right)$ 把 $y$ 表示出来,就得到 $y=\phi \left(x\right)$ . 又表达式 $y=f\left(x\right)$ 与 $x=\phi \left(y\right)$ 等价,由此可以得到如下重要公式:

$$\begin{array}{}\text{(2.13)}& f\left(\phi \left(y\right)\right)=y\text{ 和 }\phi \left(f\left(x\right)\right)=x.\end{array}$$

反函数 $y=\phi \left(x\right)$ 的图像可由 $y=f\left(x\right)$ 的图像沿直线 $y=x$ 反射得到 (图 2.6).

$◼$ 函数 $y=f\left(x\right)={\mathrm{e}}^x\left(D:-\mathrm{\infty }<x<+\mathrm{\infty },W:y>0\right)$ 显然与 $x=\phi \left(y\right)=\ln y$ 等价, 且每个严格单调函数都有反函数.

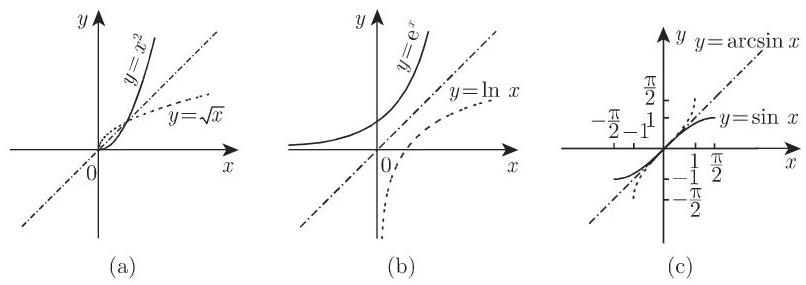
反函数举例:

$◼\mathbf{A}$: $y=f\left(x\right)=x^2$ ,其中 $D:x\ge 0,W:y\ge 0$ ;

$$y=\phi \left(x\right)=\sqrt{x}\text{,其中}D:x\ge 0,W:y\ge 0\text{.}$$

$◼\mathbf{B}$: $y=f\left(x\right)={\mathrm{e}}^x$ ,其中 $D:-\mathrm{\infty }<x<+\mathrm{\infty },W:y>0$ ;

$$y=\phi \left(x\right)=\ln x\text{,其中}D:x>0,W:-\mathrm{\infty }<y<+\mathrm{\infty }\text{.}$$

$◼\mathbf{C}$: $y=f\left(x\right)=\sin x$ ,其中 $D:-\frac{\pi }{2}\le x\le \frac{\pi }{2},W:-1\le y\le 1$ ;

$$y=\phi \left(x\right)=\arcsin x\text{,其中}D:-1\le x\le 1,W:-\frac{\pi }{2}\le y\le \frac{\pi }{2}\text{.}$$

注 (1) 若函数 $f$ 在区间 $I\subset D$ 上严格单调,则在此区间存在反函数 $f^{-1}$ .

(2) 若非单调函数在严格单调部分能够进行分割, 则在这些部分存在相应的反函数.