8.3.3 一般类型的线积分

8.3.3.1 定义

一般类型的线积分是沿一条曲线所有投影的第二类线积分之和. 设沿已知曲线 $C$ 给出两个二元函数 $P\left(x,y\right)$ 和 $Q\left(x,y\right)$ ,或三个三元函数 $P\left(x,y,z\right),Q\left(x,y,z\right)$ 和 $R\left(x,y,z\right)$ ,且相应的第二类线积分存在,则对平面曲线或空间曲线,下面公式成立.

1. 平面曲线

$$\begin{array}{}\text{(8.118a)}& {\int }_{\left(C\right)}\left(P\mathrm{d}x+Q\mathrm{d}y\right)={\int }_{\left(C\right)}P\mathrm{d}x+{\int }_{\left(C\right)}Q\mathrm{d}y.\end{array}$$

2. 空间曲线

$$\begin{array}{}\text{(8.118b)}& {\int }_{\left(C\right)}\left(P\mathrm{d}x+Q\mathrm{d}y+R\mathrm{d}z\right)={\int }_{\left(C\right)}P\mathrm{d}x+{\int }_{\left(C\right)}Q\mathrm{d}y+{\int }_{\left(C\right)}R\mathrm{d}z.\end{array}$$

在向量分析一章 (参见第 938 页 13.3.1.1) 将会讨论一般类型线积分的向量表示及其在力学中的应用.

8.3.3.2 一般类型线积分的性质

1. 积分路径的分解

用曲线 $\stackrel{⏜}{AB}$ 上的一点 $M$ ,甚至是 $\stackrel{⏜}{AB}$ 外一点 $M$ (图 8.26),可以把积分分解成两部分:

$$\begin{array}{}\text{(8.119)}& {\int }_{\stackrel{⏜}{AB}}\left(P\mathrm{d}x+Q\mathrm{d}y\right)={\int }_{\stackrel{⏜}{AM}}\left(P\mathrm{d}x+Q\mathrm{d}y\right)+{\int }_{\stackrel{⏜}{MB}}\left(P\mathrm{d}x+Q\mathrm{d}y\right).\end{array}$$

2. 积分路径反向

积分变号:

$$\begin{array}{}\text{(8.120)}& {\int }_{\stackrel{⏜}{AB}}\left(P\mathrm{d}x+Q\mathrm{d}y\right)=-{\int }_{\stackrel{⏜}{BA}}{(P\mathrm{d}x+Q\mathrm{d}y)}^{\left(1\right)}\end{array}$$

3. 路径的相关性

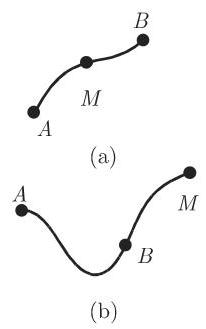
一般地, 线积分的值不仅与起点有关, 还和积分路径有关 (图 8.27):

$$\begin{array}{}\text{(8.121)}& {\int }_{\stackrel{⏜}{AMB}}\left(P\mathrm{d}x+Q\mathrm{d}y\right)\ne {\int }_{\stackrel{⏜}{ADB}}{(P\mathrm{d}x+Q\mathrm{d}y)}^{\text{②}}\end{array}$$

$◼\mathbf{A}$: $I={\int }_{\left(C\right)}\left(xy\mathrm{d}x+yz\mathrm{d}y+zx\mathrm{d}z\right)$ ,其中 $C$ 为螺旋线 $x=a\cos t,y=a\sin t,z=$ $bt$ (参见第 348 页螺旋线) 从 $t_0=0$ 到 $T=2\pi$ 的一圈:

$$I={\int }_0^{2\pi }\left(-a^3{\sin }^{2}t\cos t+a^{2}bt\sin t\cos t+a{b}^{2}t\cos t\right)\mathrm{d}t=-\frac{\pi a^{2}b}{2}.$$

$◼\mathbf{B}$: $I={\int }_{\left(C\right)}\left[y^2\mathrm{d}x+\left(xy-x^2\right)\mathrm{d}y\right]$ ,其中 $C$ 为抛物线 $y^2=9x$ 上位于点 $A\left(0,0\right)$ 和 $B\left(1,3\right)$ 间的弧段:

$$I={\int }_0^3\left[\frac{2}{9}{y}^3+\left(\frac{y^3}{9}-\frac{y^4}{81}\right)\right]\mathrm{d}y=6\frac{3}{20}.$$

---

① 对三元函数有类似公式成立.

② 同①.

---

8.3.3.3 沿闭曲线的积分

(1) 沿闭曲线积分的概念 环路积分也称为沿曲线的围道积分, 它是沿闭合的积分路径 $C$ 的线积分,即积分路径的起点 $A$ 和终点 $B$ 相同,通常记为

$$\begin{array}{}\text{(8.122)}& {\oint }_{\left(C\right)}\left(P\mathrm{d}x+Q\mathrm{d}y\right)\text{ 或 }{\oint }_{\left(C\right)}\left(P\mathrm{d}x+Q\mathrm{d}y+R\mathrm{d}z\right).\end{array}$$

一般而言, 该积分不等于 0 , 但是如它满足 (8.127) 中的条件或者积分在一个守恒场中进行 (参见第 941 页 13.3.1.6), 积分值等于 0. (也可参见第 941 页 13.3.1.6 中的零值围道积分. )

(2) 平面图形面积 $S$ 的计算 是应用沿闭曲线积分的典型例子,形式如下:

$$\begin{array}{}\text{(8.123)}& S=\frac{1}{2}{\oint }_{\left(C\right)}\left(x\mathrm{d}y-y\mathrm{d}x\right),\end{array}$$

其中 $C$ 为平面图形的边界曲线. 若积分路径逆时针方向,则积分为正.