19.6.1 多项式插值

插值的基本问题是通过一系列点 $\left(x_v,y_v\right)\left(v=0,1,\cdots ,n\right)$ 来拟合曲线. 它可以通过曲线拟合小段图示,或通过在所谓插值点 $x_v$ 取 $y_v$ 值的函数 $g\left(x\right)$ 数值化,即 $g\left(x\right)$ 满足插值条件

$$\begin{array}{}\text{(19.159)}& g\left(x_{\nu }\right)=y_{\nu }\left(\nu =0,1,2,\cdots ,n\right).\end{array}$$

插值函数最早用多项式, 对周期函数或用所谓三角多项式. 后一种情况为三角插值 (参见第 1287 页 19.6.4.1,2.). 有 $n+1$ 个插值点,插值阶为 $n$ ,则插值多项式的最高阶至多为 $n$ . 因为随着次数增加,多项式可能产生强烈的振荡,故通常不需要高阶插值. 插值区间能划分为子区间进行样条插值 (参见第 1293 页 19.7).

19.6.1.1 牛顿插值公式

为解插值问题 (19.159),考虑如下形式的 $n$ 次多项式

$$g\left(x\right)=p_n\left(x\right)=a_0+a_1\left(x-x_0\right)+a_2\left(x-x_0\right)\left(x-x_1\right)+\cdots$$$$\begin{array}{}\text{(19.160)}& +a_n\left(x-x_0\right)\left(x-x_1\right)\cdots \left(x-x_{n-1}\right).\end{array}$$

这称为牛顿插值公式, 因为插值条件 (19.159) 导致三角矩阵的线性方程组, 故容易计算系数 $a_i\left(i=0,1,\cdots ,n\right)$ .

$◼$ 对于 $n=2$ ,由 (19.159) 得到附加的方程组. 插值多项式 $p_n\left(x\right)$ 由插值条件 (19.159) 唯一确定.

$$p_2\left(x_0\right)=a_0=y_0,$$$$p_2\left(x_1\right)=a_0+a_1\left(x_1-x_0\right)=y_1,$$$$p_2\left(x_2\right)=a_0+a_1\left(x_1-x_0\right)+a_2\left(x_1-x_0\right)\left(x_2-x_1\right)=y_2.$$

函数值的计算可以由霍纳格式 (参见第 1237 页 19.1.2.1) 简化.

19.6.1.2 拉格朗日插值公式

$n$ 次多项式可以用 $n+1$ 个点 $\left(x_v,y_v\right)\left(v=0,1,\cdots ,n\right)$ 的拉格朗日公式来拟合:

$$\begin{array}{}\text{(19.161)}& g\left(x\right)=p_n\left(x\right)=\sum _{\mu =0}^n{y}_{\mu }{L}_{\mu }\left(x\right).\end{array}$$

这里 $L_{\mu }\left(x_v\right)\left(v=0,1,\cdots ,n\right)$ 为拉格朗日插值多项式. 方程 (19.161) 满足插值条件 (19.159), 因为

$$\begin{array}{}\text{(19.162)}& L_{\mu }\left(x_v\right)={\delta }_{\mu v}=\{\begin{array}{ll}1,& \mu =\nu ,\\ 0,& \mu \ne \nu ,\end{array}\end{array}$$

其中 ${\delta }_{\mu \nu }$ 为克罗内克 (Kronecker) 记号. 拉格朗日插值多项式定义为

$$L_{\mu }=\frac{\left(x-x_0\right)\left(x-x_1\right)\cdots \left(x-x_{\mu -1}\right)\left(x-x_{\mu +1}\right)\cdots \left(x-x_n\right)}{\left(x_{\mu }-x_0\right)\left(x_{\mu }-x_1\right)\cdots \left(x_{\mu }-x_{\mu -1}\right)\left(x_{\mu }-x_{\mu +1}\right)\cdots \left(x_{\mu }-x_n\right)}$$$$\begin{array}{}\text{(19.163)}& =\prod _{\begin{array}{c}\nu =0\\ \nu \ne \mu \end{array}}^n\frac{x-x_{\nu }}{x_{\mu }-x_{\nu }}\end{array}$$

• 由下表中给出的点来拟合多项式.

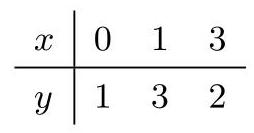
利用拉格朗日插值多项式 (19.161):

$$L_0\left(x\right)=\frac{\left(x-1\right)\left(x-3\right)}{\left(0-1\right)\left(0-3\right)}=\frac{1}{3}\left(x-1\right)\left(x-3\right),$$$$L_1\left(x\right)=\frac{\left(x-0\right)\left(x-3\right)}{\left(1-0\right)\left(1-3\right)}=-\frac{1}{2}x\left(x-3\right),$$$$L_2\left(x\right)=\frac{\left(x-0\right)\left(x-1\right)}{\left(3-0\right)\left(3-1\right)}=\frac{1}{6}x\left(x-1\right);$$$$p_2\left(x\right)=1\cdot L_0\left(x\right)+3\cdot L_1\left(x\right)+2\cdot L_2\left(x\right)=-\frac{5}{6}{x}^2+\frac{17}{6}x+1.$$

拉格朗日插值多项式显式且线性依赖于函数值 $y_{\mu }$ . 这在理论上是重要的 (例如参见第 1262 页 19.4.1.3,3. 亚当斯-巴什福斯法则). 但在实际计算中, 拉格朗日插值公式并不常用.

19.6.1.3 艾特肯-内维尔插值

在许多实际情况中,我们并不需要多项式 $p_n\left(x\right)$ 的显形式,只需要插值区域内给定点 $x$ 处的值就可以. 这些函数值可以由艾特肯 (Aitken) 和内维尔 (Neville) 发展的递推方法得到. 记号

$$\begin{array}{}\text{(19.164)}& p_n\left(x\right)=p_{0,1,\cdots ,n}\left(x\right)\end{array}$$

表示以 $x_0,x_1,\cdots ,x_n$ 为插值点的 $n$ 次多项式. 注意到

$$\begin{array}{}\text{(19.165)}& p_{0,1,\cdots ,n}\left(x\right)=\frac{\left(x-x_0\right)p_{1,2,\cdots ,n}\left(x\right)-\left(x-x_n\right)p_{0,1,2,\cdots ,n-1}\left(x\right)}{x_n-x_0},\end{array}$$

即函数值 $p_{0,1,\cdots ,n}\left(x\right)$ 可由两个次数低于 $n-1$ 的多项式 $p_{1,2,\cdots ,n}\left(x\right)$ 和 $p_{0,1,\cdots ,n-1}\left(x\right)$ 的线性组合得到. 应用 (19.165),对于 $n=4$ 的情况有

$$\begin{array}{}\text{(19.166)}& \begin{array}{l}{x}_0\mid y_0=p_0\\ x_1\mid y_1=p_1{p}_{01}\\ x_2\mid y_2=p_2{p}_{12}{p}_{012}\\ x_3\mid y_3=p_3{p}_{23}{p}_{123}{p}_{0123}\\ x_4\mid y_4=p_4{p}_{34}{p}_{234}{p}_{11234}{p}_{01234}{p}_{01234}=p_4\left(x\right).\end{array}\end{array}$$

逐列计算 (19.166) 的元素. 格式中的新值由其左边及左上的数值得到.

$$\begin{array}{}\text{(19.167a)}& p_{23}=\frac{\left(x-x_2\right)p_3-\left(x-x_3\right)p_2}{x_3-x_2}=p_3+\frac{x-x_3}{x_3-x_2}\left(p_3-p_2\right),\end{array}$$$$\begin{array}{}\text{(19.167b)}& p_{123}=\frac{\left(x-x_1\right)p_{23}-\left(x-x_3\right)p_{12}}{x_3-x_1}=p_{23}+\frac{x-x_3}{x_3-x_1}\left(p_{23}-p_{12}\right),\end{array}$$$$\begin{array}{}\text{(19.167c)}& p_{1234}=\frac{\left(x-x_1\right)p_{234}-\left(x-x_4\right)p_{123}}{x_4-x_1}=p_{234}+\frac{x-x_4}{x_4-x_1}\left(p_{234}-p_{123}\right).\end{array}$$

为在计算机上实施艾特肯-内维尔 (Aitken-Neville) 算法,只需引进有 $n+1$ 个分量的向量 $\underset{―}{p}$ (见 [19.7]),根据规则依次取 (19.166) 中的列值,第 $k$ 列的值 $p_{i-k,i-k+1,\cdots ,i}$ $\left(i=k,k+1,\cdots ,n\right)$ 正是 $\underset{―}{p}$ 的第 $i$ 个分量 $p_i$ . 由于必须向下计算 (19.166) 的列, 故 $\underset{―}{p}$ 包含所有必要的数值. 算法有如下两步:

(1) 对 $i=0,1,\cdots ,n$ ,设 $p_i=y_i$ .(19.168a)

(2) 对 $k=1,2,\cdots ,n$ 及 $i=n,n-1,\cdots ,k$ ,计算 $p_i=p_i+\frac{x-x_i}{x_i-x_{i-k}}\left(p_i-p_{i-1}\right)$ .(19.168b)

在结束 (19.168b) 的计算后,我们得到元素 $p_n$ 在点 $x$ 处要求的函数值 $p_n\left(x\right)$ .