Appearance
2.1.2 实函数的定义方法
2.1.2.1 函数的定义
函数可以按不同方式来定义, 如值表、图示 (曲线)、公式 (解析表达式), 或不同公式构成的分段函数. 其中的自变量只有在属于解析表达式的定义域时, 函数才有意义, 即函数取得唯一有限实值. 当没有给出定义域时, 认为定义域为使得该函数有意义的最大集合.
2.1.2.2 函数的解析表示
通常采用如下三种形式:
1. 显形式
2. 隐形式
此时对每个
3. 参数形式
注 参数形式的函数有时并不能表示为不含参数的显方程或隐方程.
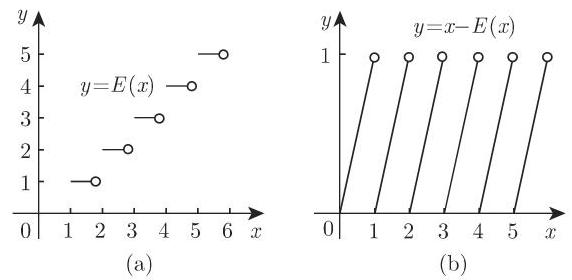
分段函数举例:
函数
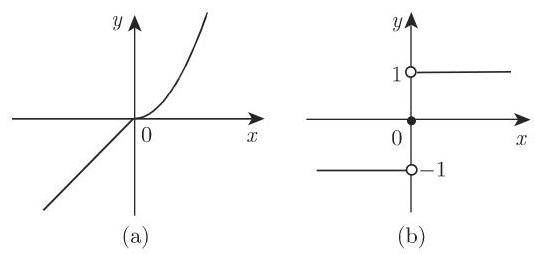
号函数.