16.3.5 蒙特卡罗方法

16.3.5.1 模拟

模拟法立足于构建等价的数学模型. 通过计算机分析这些模型很容易. 在这种情形下, 可使用数字模拟. 当一定数量的模型被随机选取时, 蒙特卡罗方法给出了一个特殊案例. 这些随机元素可使用随机数选取.

16.3.5.2 随机数

随机数是满足特定分布的某些随机量的实现 (参见第 1061 页 16.2.2). 通过这种方式可区分不同类型的随机数.

1. 均匀分布的随机数

均匀分布于区间 $\left[0,1\right]$ 的随机数,是密度函数为 $f_0\left(x\right)$ 、分布函数为 $F_0\left(x\right)$ 的随机变量 $X$ 的实现:

$$\begin{array}{}\text{(16.168)}& f_0\left(x\right)=\{\begin{array}{ll}1,& 0\le x\le 1,\\ 0,& \text{ 其他,}\end{array}{F}_0\left(x\right)=\{\begin{array}{ll}0,& 0\le x,\\ x,& 0<x\le 1,\\ 1,& x\ge 1.\end{array}\end{array}$$

(1)平方取中法 冯・诺伊曼提出了一种产生随机数的简便方法, 也称为平方取中法,它从一个 $2n$ 位小数 $z\in \left(0,1\right)$ 开始. 首先构造 $z^2$ ,得到一个 $4n$ 位小数. 去掉其前 $n$ 位数字和后 $n$ 位数字,再次得到一个 $2n$ 位数. 重复上述程序,进一步产生新数. 通过这种方式即产生了 $\left[0,1\right]$ 区间上的 $2n$ 位小数,可视为服从均匀分布的随机数. 根据计算机可表示的最大数选取 $2n$ 的值,比如 $2n=10$ . 由于该程序产生了比它更小的数字, 故很少使用, 目前已发展了其他一些不同的方法.

$◼2n=4$

$$z=z_0=0,1234,z_0^2=0.01522756,$$$$z=z_1=0,5227,z_0^2=0.27321529,$$$$z=z_2=0,3215\text{等.}$$

最初的三个随机数是 $z_0,z_1$ 和 $z_2$ .

(2) 同余法 所谓的同余法应用广泛: 整数序列 $z_i\left(i=0,1,2,\cdots \right)$ 由递推公式

$$\begin{array}{}\text{(16.169)}& z_{i+1}\equiv c\cdot z_i\mathrm{mod}m\end{array}$$

生成,其中, $z_0$ 是任意正数, $c$ 和 $m$ 表示正整数,必须合理选取. 对于 $z_{i+1}$ ,可取满足同余式 (16.169) 的最小非负整数. 数 $\frac{z_i}{m}$ 位于 0 到 1 之间,可作为均匀分布随机数.

(3) 注 a) 选取 $m=2^r$ ,其中 $r$ 是计算机语言中的二进制数,例如 $r=40$ ,则依 $\sqrt{m}$ 的次序选取数 $c$ .

b) 随机数生成器使用特定算法, 可产生所谓伪随机数.

c) 计算器以及计算机中的 “ran” 或 “rand” 键用于生成随机数.

2. 服从其他分布的随机数

为得到服从任意分布函数 $F\left(x\right)$ 的随机数,可使用下述程序: 对于区间 $\left[0,1\right]$ 上的均匀分布随机数序列 ${\xi }_1,{\xi }_2,\cdots$ ,利用它们构造数 ${\eta }_i=F^{-1}\left({\xi }_i\right),i=1,2,\cdots$ ,其中 $F^{-1}\left(x\right)$ 是分布函数 $F\left(x\right)$ 的逆函数,则可得到

$$\begin{array}{}\text{(16.170)}& P\left({\eta }_i\le x\right)=P\left(F^{-1}\left({\xi }_i\right)\le x\right)=P\left({\xi }_i\le F\left(x\right)\right)={\int }_0^{F\left(x\right)}{f}_0\left(t\right)\mathrm{d}t=F\left(x\right),\end{array}$$

即随机数 ${\eta }_1,{\eta }_2,\cdots$ 服从分布函数为 $F\left(x\right)$ 的分布.

3. 随机数表及其应用

(1) 构造 可通过下述方式构造随机数表. 在 10 个完全相同的筹码上标注数字 $0,1,2,\cdots ,9$ ,把它们放在一个盒子中并摇匀. 选取其中之一,将其对应的号码写到表格中, 然后把筹码再次放到盒子中摇匀, 选取第二个. 通过这种方式即产生一个随机数序列, 可作为一组记录到表格中 (使用更方便). 在 1464 页表 21.21 中, 4 位随机数形成一组.

在程序中,必须保证数字 $0,1,2,\cdots ,9$ 总是等概率出现.

(2)随机数表的应用 举例说明随机数表的应用.

• 假设从 $N=250$ 项的总体中随机选取 $n=20$ 项. 总体中的对象记数为 000 到 249. 然后在 1464 页表 21.21 的任意列或行中选取一个数, 明确如何选取其余 19 个数的规则, 如纵向、横向或对角线方向. 只要最初的 3 个数字取自于随机数, 且生成的数小于 250 个, 该方法即可使用.

16.3.5.3 蒙特卡罗模拟举例

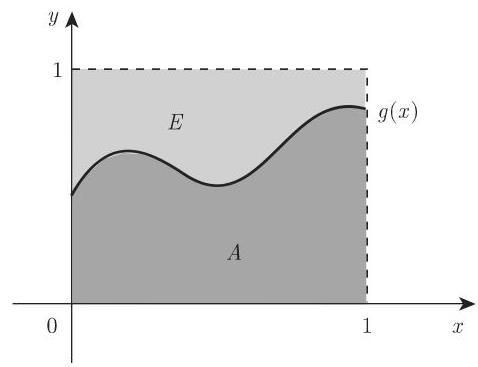
求积分

$$\begin{array}{}\text{(16.171)}& I={\int }_0^{1}g\left(x\right)\mathrm{d}x\end{array}$$

的近似值是模拟中应用均匀分布随机数的一个实例. 下面讨论两种求解方法.

1. 运用频率

设 $0\le g\left(x\right)\le 1$ . 通过积分变换总可保证该条件成立 (参见第 1103 页 (16.175)) 则积分 $I$ 是单位正方形 $E$ 内的区域面积 (图 16.16). 考虑区间 $\left[0,1\right]$ 内均匀分布随机数序列的数值,把它们成对地作为单位正方形 $E$ 内点的坐标,可得到 $n$ 个点 $P_i\left(i=1,2,\cdots ,n\right)$ . 用 $m$ 表示区域 $A$ 内点的数量,则可使用频率把积分表示为 (参见第 1057 页 16.2.1.2)

$$\begin{array}{}\text{(16.172)}& {\int }_0^{1}g\left(x\right)\mathrm{d}x\approx \frac{m}{n}.\end{array}$$

使用 (16.172) 的比值, 欲得到较好的精确度, 需要大量随机数. 这正是人们探究有可能提高精度的原因. 方法之一是下述蒙特卡罗方法, 另外一些方法可查阅相关文献 (参见文献 [16.19]).

2. 利用均值逼近

为求解式 (16.171),可从 $n$ 个均匀分布随机数 ${\xi }_1,{\xi }_2,\cdots ,{\xi }_n$ 出发,作为均匀分布随机变量 $X$ 的实现. 则 $g_i=g\left({\xi }_i\right)\left(i=1,2,\cdots ,n\right)$ 是随机变量 $g\left(X\right)$ 的实现, 根据第 1063 页的公式 (16.49a,16.49b), $g\left(X\right)$ 的期望是

$$\begin{array}{}\text{(16.173)}& E\left(g\left(X\right)\right)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}g\left(x\right)f_0\left(x\right)\mathrm{d}x={\int }_0^{1}g\left(x\right)\mathrm{d}x\approx \frac{1}{n}\sum _{i=1}^n{g}_i.\end{array}$$

这种方法使用样本得到均值, 也称为普通蒙特卡罗方法.

16.3.5.4 在数值数学中应用蒙特卡罗方法

1. 估计多重积分

首先说明如何把单变量的定积分 (16.174a) 变换为包含积分 (16.174b) 的式子.

$$\begin{array}{}\text{(16.174a)}& I^{\ast }={\int }_a^{b}h\left(x\right)\mathrm{d}x\end{array}$$$$\begin{array}{}\text{(16.174b)}& I={\int }_0^{1}g\left(x\right)\mathrm{d}x\text{ 且 }0\le g\left(x\right)\le 1.\end{array}$$

引入下述记号:

$$\begin{array}{}\text{(16.175)}& x=a+\left(b-a\right)u,m=\underset{x\in \left[a,b\right]}{min}h\left(x\right),M=\underset{x\in \left[a,b\right]}{max}h\left(x\right),\end{array}$$

即可使用 16.3.5.3 中给出的蒙特卡罗方法, 则 (16.174a) 变形为

$$\begin{array}{}\text{(16.176)}& I^{\ast }=\left(M-m\right)\left(b-a\right){\int }_0^1\frac{h\left(a+\left(b-a\right)u\right)-m}{M-m}\mathrm{d}u+\left(b-a\right)m,\end{array}$$

其中被积函数 $\frac{h\left(a+\left(b-a\right)u\right)-m}{M-m}=g\left(u\right)$ 满足 $0\le g\left(u\right)\le 1$ .

$◼$ 通过双重积分

$$\begin{array}{}\text{(16.177)}& V={\iint }_{S}h\left(x,y\right)\mathrm{d}x\mathrm{d}y\text{ 且 }h\left(x,y\right)\ge 0\end{array}$$

的例子,说明如何使用蒙特卡罗方法近似估计多重积分. $S$ 表示由不等式 $a\le x\le b$ 和 ${\phi }_1\left(x\right)\le y\le {\phi }_2\left(x\right)$ 所围成的平面区域,其中 ${\phi }_1\left(x\right)$ 和 ${\phi }_2\left(x\right)$ 表示已知函数. 则 $V$ 可视为与 $xy$ 平面垂直、上表面为 $h\left(x,y\right)$ 的圆柱体的体积. 若 $h\left(x,y\right)\le e$ ,则圆柱体位于由不等式 $a\le x\le b,c\le y\le d,0\le z\le e\left(a,b,c,d,e\text{为常数}\right)$ 所围成的立体 $Q$ 内. 类似于 (16.175) 进行变换,由 (16.177) 可得到包含积分的表达式

$$\begin{array}{}\text{(16.178)}& V^{\ast }={\iint }_{S^{\ast }}g\left(u,v\right)\mathrm{d}u\mathrm{d}v\text{ 且 }0\le g\left(u,v\right)\le 1,\end{array}$$

其中 $V^{\ast }$ 是三维立方体内柱体 $K^{\ast }$ 的体积. 利用蒙特卡罗方法按照下述方式可求积分 (16.178) 的近似值:

区间 $\left[0,1\right]$ 内均匀分布随机数序列的三元数组,可视为立方体内点 $P_i(i=$ $1,2,\cdots ,n)$ 的坐标,查找 $P_i$ 中位于柱体 $K^{\ast }$ 内点的个数. 若 $m$ 个点在 $K^{\ast }$ 内,与 (16.172) 类似, 可得

$$\begin{array}{}\text{(16.179)}& V^{\ast }\approx \frac{m}{n}\end{array}$$

注 当定积分中只有一个积分变量时, 可使用第 1252 页 19.3 中的方法. 若估计多重积分, 仍常推荐用蒙特卡罗方法.

2. 使用随机游动过程求解偏微分方程

借助随机游动过程, 蒙特卡罗方法可用于近似求解偏微分方程.

a) 边值问题举例 考虑下述边值问题作为例子:

$$\begin{array}{}\text{(16.180a)}& \mathrm{\Delta }u=\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}=0,\left(x,y\right)\in G,\end{array}$$$$\begin{array}{}\text{(16.180b)}& u\left(x,y\right)=f\left(x,y\right),\left(x,y\right)\in \mathrm{\Gamma }.\end{array}$$

$G$ 是 $xy$ 平面内的单连通区域; $\mathrm{\Gamma }$ 表示 $G$ 的边界 (图 16.17). 与第 1268 页 19.5.1 中的差分法类似,用二次格覆盖 $G$ ,不失一般性,此处可假定步长 $h=1$ .

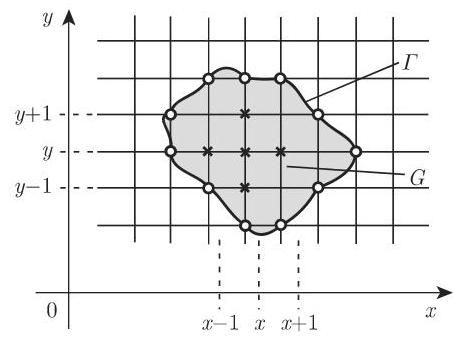
通过这种方式可得到内部格点 $P\left(x,y\right)$ 和边界点 $R_i$ . 边界点 $R_i$ 同时也是格点, 在下面的讨论中可视为 $G$ 的边界 $\mathrm{\Gamma }$ 的点,即

$$\begin{array}{}\text{(16.181)}& u\left(R_i\right)=f\left(R_i\right)\left(i=1,2,\cdots ,N\right).\end{array}$$

b) 求解原则 设想粒子从内部点 $P\left(x,y\right)$ 开始随机游动,也就是说:

(1)粒子从 $P\left(x,y\right)$ 向四个临近点中的某一个随机移动. 假设移向每一个格点的概率是 $1/4$ .

(2) 如果粒子到达边界点 $R_i$ ,则随机游动以概率 1 终止.

可以证明,无论粒子从哪一内部格点 $P$ 开始,经过一定步数后,都将以概率 1 到达边界点 $R_i$ . 用

$$\begin{array}{}\text{(16.182)}& p\left(P,R_i\right)=p\left(\left(x,y\right),R_i\right)\end{array}$$

表示始于 $P\left(x,y\right)$ 、将在边界点 $R_i$ 终止的随机游动的概率,则可得到

$$\begin{array}{}\text{(16.183)}& p\left(R_i,R_i\right)=1,p\left(R_i,R_j\right)=0,i\ne j,\end{array}$$$$p\left(\left(x,y\right),R_i\right)$$$$=\frac{1}{4}\left[p\left(\left(x-1,y\right),R_i\right)+p\left(\left(x+1,y\right),R_i\right)+p\left(\left(x,y-1\right),R_i\right)+p\left(\left(x,y+1\right),R_i\right)\right]$$

(16.184)

(16.184) 是关于 $p\left(\left(x,y\right),R_i\right)$ 的差分方程. 若 $n$ 个随机游动从点 $P\left(x,y\right)$ 开始. 其中 $m_i$ 个在 $R_i\left(m_i\le n\right)$ 终止,则

$$\begin{array}{}\text{(16.185)}& p\left(\left(x,y\right),R_i\right)\approx \frac{m_i}{n}.\end{array}$$

(16.185) 给出了差分方程 (16.180a) 的近似解, 其边界条件为 (16.181). 若进行替换

$$\begin{array}{}\text{(16.186)}& v\left(P\right)=v\left(x,y\right)=\sum _{i=1}^{N}f\left(R_i\right)p\left(\left(x,y\right),R_i\right),\end{array}$$

则满足边界条件 (16.180b). 根据 (16.184),有 $v\left(R_j\right)=\sum _{i=1}^{N}f\left(R_i\right)p\left(R_j,R_i\right)=f\left(R_j\right)$ .

为计算 $v\left(x,y\right)$ ,用 $f\left(R_i\right)$ 乘以(16.184),求和将得到下述关于 $v\left(x,y\right)$ 的差分方程:

$$\begin{array}{}\text{(16.187)}& v\left(x,y\right)=\frac{1}{4}\left[v\left(x-1,y\right)+v\left(x+1,y\right)+v\left(x,y-1\right)+v\left(x,y+1\right)\right].\end{array}$$

若 $n$ 个随机游动从点 $P\left(x,y\right)$ 开始,其中 $m_j$ 个终止于边界点 $R_i(i=1,2,\cdots$ , $N)$ ,则在点 $P\left(x,y\right)$ 处边值问题(16.180a,16.180b)的近似值为

$$\begin{array}{}\text{(16.188)}& v\left(x,y\right)\approx \frac{1}{n}\sum _{i=1}^n{m}_{i}f\left(R_i\right).\end{array}$$

16.3.5.5 蒙特卡罗方法的进一步应用

作为随机模拟, 蒙特卡罗方法有时也称为统计试验方法 广泛应用于诸多不同领域. 例如:

• 核技术: 穿过材料层的中子数.

• 通信: 分离信号和噪声.

• 运筹学: 排队系统, 过程设计, 库存控制, 服务系统.

对这些问题的细节讨论可参见文献 [16.19], [16.23].