2.18.1 定义及其表示

2.18.1.1 多元函数的表示

设函数 $u$ 含有 $n$ 个独立的变元 $x_1,x_2,\cdots ,x_n$ ,若对于任意一组给定的值, $u$ 都有唯一确定的值与之对应,则称 $u$ 为 $n$ 元函数. 根据变量的个数,如两个、三个或 $n$ 个,可以写成

$$\begin{array}{}\text{(2.276)}& u=f\left(x,y\right),u=f\left(x,y,z\right),u=f\left(x_1,x_2,\cdots ,x_n\right).\end{array}$$

赋予这 $n$ 个独立变量值后,得到一个变量数组,它可看成 $n$ 维空间中的一个点. 单个的独立变量称为自变量; 有时整个 $n$ 元数组也称为函数的自变量.

函数值举例:

$◼\mathbf{A}$: 当 $x=2,y=3$ 时,函数 $u=f\left(x,y\right)=x{y}^2$ 的值 $f\left(2,3\right)=2\cdot 3^2=18$ .

$◼\mathbf{B}$: 当 $x=3,y=4,z=3,t=1$ 时,函数 $u=f\left(x,y,z,t\right)=x\ln \left(y-zt\right)$ 的值$f\left(3,4,3,1\right)=3\ln \left(4-3\cdot 1\right)=0.$

2.18.1.2 多元函数的几何表示

1. 变量数组的表示

两个自变量 $x,y$ 的数组在笛卡儿坐标系中表示平面上的一点; 三个自变量 $x,y,z$ 的数组在三维笛卡儿坐标系中表示坐标为(x, y, z)的一点. 显然,在我们所理解的三维空间中, 无法表示具有四个或更多个坐标的数组.

与三维空间中的情况类似,含 $n$ 个变量的数组 $x_1,x_2,\cdots ,x_n$ 可以看成 $n$ 维空间中的一点,其笛卡儿坐标为 $\left(x_1,x_2,\cdots ,x_n\right)$ . 在 2.18.1.1 例B中,4 个变量定义了四维空间中的一点,坐标为 $x=3,y=4,z=3,t=1$ .

2. 二元函数 $u=f\left(x,y\right)$ 的表示

a) 与一元函数的图示类似, 含两个独立变量的函数可用三维空间的一曲面来表示 (图 2.100, 也可参见第 350 页 3.6.3.1). 把定义域中自变量的值作为笛卡儿坐标系中点的前两个坐标,函数值 $u=f\left(x,y\right)$ 作为第三个坐标,这些点就构成了三维空间中的一个曲面.

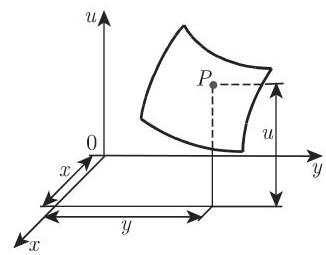
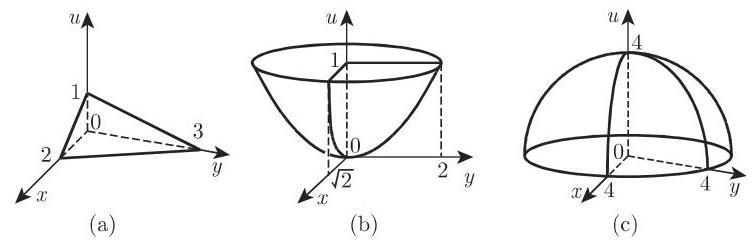
函数曲面举例:

$◼\mathbf{A}$: $u=1-\frac{x}{2}-\frac{y}{3}$ 表示一平面 (图 2.101(a),也可参见第 293 页 3.5.3.10).

$◼\mathbf{B}$: $u=\frac{x^2}{2}+\frac{y^2}{4}$ 表示一椭圆抛物面 (图 2.101(b),也可参见第 303 页 3.5.3.13,5.).

$◼\mathbf{C}$: $u=\sqrt{16-x^2-y^2}$ 表示一半径 $r=4$ 的半球面 (图 2.101(c)).

b) 利用平行于坐标面的平面与曲面 $u=f\left(x,y\right)$ 相截得到的交线,可以描绘出函数 $u=f\left(x,y\right)$ 表示的曲面形状. 交线 $u$ 等于常数称为等高线.

$◼$ 在图 2.101(b), (c) 中等高线分别为椭圆和同心圆 (没有在图示中标明).

注 在三维空间中无法表示三元或更多变元的函数. 与三维空间中的曲面类似,在 $n$ 维空间中使用超曲面的概念.