15.3.2 使用傅里叶变换求解微分方程

与拉普拉斯变换类似, 由于傅里叶变换可把微分方程转化为简单形式, 故傅里叶变换的一个重要应用是求解微分方程. 在常微分方程情况, 可得到代数方程, 在偏微分方程情况, 可得到常微分方程.

15.3.2.1 线性常微分方程

微分方程 $y^{\prime }\left(t\right)+ay\left(t\right)=f\left(t\right)$ ,其中

$$\begin{array}{}\text{(15.96a)}& f\left(t\right)=\{\begin{array}{ll}1,& \left|t\right|<t_0\\ 0,& \left|t\right|\ge t_0\end{array}\end{array}$$

即图 15.21 中的函数 $f\left(t\right)$ ,通过傅里叶变换

$$\begin{array}{}\text{(15.96b)}& \mathcal{F}\{y\left(t\right)\}=Y\left(\omega \right).\end{array}$$

微分方程转化成代数方程

$$\begin{array}{}\text{(15.96c)}& \mathrm{i}\omega Y+aY=\frac{2\sin \omega t_0}{\omega },\end{array}$$

解得

$$\begin{array}{}\text{(15.96d)}& Y\left(\omega \right)=2\frac{\sin \omega t_0}{\omega \left(a+\mathrm{i}\omega \right)}.\end{array}$$

逆变换给出

$$\begin{array}{}\text{(15.96e)}& y\left(t\right)={\mathcal{F}}^{-1}\{Y\left(\omega \right)\}={\mathcal{F}}^{-1}\left\{2\frac{\sin \omega t_0}{\omega \left(a+\mathrm{i}\omega \right)}\right\}=\frac{1}{\pi }{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{{\mathrm{e}}^{\mathrm{i}\omega t}\sin \omega t_0}{\omega \left(a+\mathrm{i}\omega \right)}\mathrm{d}\omega ,\end{array}$$

且.

$$y\left(t\right)=\{\begin{array}{ll}0,& -\mathrm{\infty }<t<-t_0,\\ \frac{1}{a}\left[1-{\mathrm{e}}^{-a\left(t+t_0\right)}\right],& -t_0\le t\le +t_0,\\ \frac{1}{a}\left[{\mathrm{e}}^{-a\left(t-t_0\right)}-{\mathrm{e}}^{-a\left(t-t_0\right)}\right],& t_0<t<+\mathrm{\infty }.\end{array}$$

(15.96f) ①

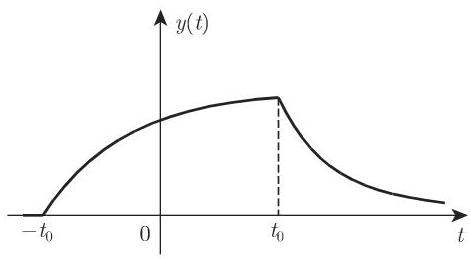
图 15.26 给出了函数(15.96f)的图像.

15.3.2.2 偏微分方程

1. 一般说明

偏微分方程的解至少是两个变量的函数: $u=u\left(x,t\right)$ . 由于傅里叶变换只对于一个变量进行积分,另一个变量在变换中应视为常数. 此处,变量 $x$ 为常数,对于 $t$ 进行变换:

$$\begin{array}{}\text{(15.97)}& \mathcal{F}\{u\left(x,t\right)\}={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{\mathrm{e}}^{-\mathrm{i}\omega t}u\left(x,t\right)\mathrm{d}t=U\left(x,\omega \right).\end{array}$$

在对导数的变换中,变量 $x$ 仍被视为常数:

$$\begin{array}{}\text{(15.98)}& \mathcal{F}\left\{\frac{{\partial }^{\left(n\right)}u\left(x,t\right)}{\partial t^n}\right\}={\left(\mathrm{i}\omega \right)}^n\mathcal{F}\{u\left(x,t\right)\}={\left(\mathrm{i}\omega \right)}^{n}U\left(x,\omega \right).\end{array}$$

假设关于 $x$ 的微分和傅里叶积分是可交换的:

$$\begin{array}{}\text{(15.99)}& \mathcal{F}\left\{\frac{\partial u\left(x,t\right)}{\partial x}\right\}=\frac{\partial }{\partial x}\mathcal{F}\{u\left(x,t\right)\}=\frac{\partial }{\partial x}U\left(x,\omega \right).\end{array}$$

---

①(15.96f)中,当 $t_0<t<+\mathrm{\infty }$ 时, $y\left(t\right)$ 的表达式是错误的. - 译者注

---

通过这种方式, 可得到像空间内的常微分方程. 而且, 边界条件和初始条件也可转化到像空间内.

2. 均匀介质内一维波动方程的解

(1)问题表述 在均匀介质内, 无扰动项的一维波动方程是

$$\begin{array}{}\text{(15.100a)}& u_{xx}-u_{tt}=0.\end{array}$$

像三维波动方程 (参见第 777 页 9.2.3.2), 方程 (15.100a) 是双曲线类偏微分方程. 柯西问题由下述初始条件给出

$$\begin{array}{}\text{(15.100b)}& u\left(x,0\right)=f\left(x\right)\left(-\mathrm{\infty }<x<\mathrm{\infty }\right),u_t\left(x,0\right)=g\left(x\right)\left(0\le t<\mathrm{\infty }\right).\end{array}$$

(2) 傅里叶变换 关于 $x$ 进行傅里叶变换,时间坐标保持为常数:

$$\begin{array}{}\text{(15.101a)}& \mathcal{F}\{u\left(x,t\right)\}=U\left(\omega ,t\right).\end{array}$$

由此可得

$$\begin{array}{}\text{(15.101b)}& {\left(\mathrm{i}\omega \right)}^{2}U\left(\omega ,t\right)-\frac{{\mathrm{d}}^{2}U\left(\omega ,t\right)}{\mathrm{d}{t}^2}=0,\end{array}$$

且.

$$\begin{array}{}\text{(15.101c)}& \mathcal{F}\{u\left(x,0\right)\}=U\left(\omega ,0\right)=\mathcal{F}\{f\left(x\right)\}=F\left(\omega \right),\end{array}$$$$\begin{array}{}\text{(15.101d)}& \mathcal{F}\left\{u_t\left(x,0\right)\right\}=U^{\prime }\left(\omega ,0\right)=\mathcal{F}\{g\left(x\right)\}=G\left(\omega \right).\end{array}$$$$\begin{array}{}\text{(15.101e)}& {\omega }^{2}U+U^{\prime \prime }=0.\end{array}$$

此方程是带有变换参数 $\omega$ 的关于 $t$ 的常微分方程. 该常系数微分方程的通解为

$$\begin{array}{}\text{(15.102a)}& U\left(\omega ,t\right)=C_1{\mathrm{e}}^{\mathrm{i}\omega t}+C_2{\mathrm{e}}^{-\mathrm{i}\omega t}.\end{array}$$

根据初始条件

$$\begin{array}{}\text{(15.102b)}& U\left(\omega ,0\right)=C_1+C_2=F\left(\omega \right),U^{\prime }\left(\omega ,0\right)=\mathrm{i}\omega C_1-\mathrm{i}\omega C_2=G\left(\omega \right),\end{array}$$

确定常数 $C_1$ 和 $C_2$ ,可得到

$$\begin{array}{}\text{(15.102c)}& C_1=\frac{1}{2}\left[F\left(\omega \right)+\frac{1}{\mathrm{i}\omega }G\left(\omega \right)\right],C_2=\frac{1}{2}\left[F\left(\omega \right)-\frac{1}{\mathrm{i}\omega }G\left(\omega \right)\right].\end{array}$$

因此, 解为

$$\begin{array}{}\text{(15.102d)}& U\left(\omega ,t\right)=\frac{1}{2}\left[F\left(\omega \right)+\frac{1}{\mathrm{i}\omega }G\left(\omega \right)\right]{\mathrm{e}}^{\mathrm{i}\omega t}+\frac{1}{2}\left[F\left(\omega \right)-\frac{1}{\mathrm{i}\omega }G\left(\omega \right)\right]{\mathrm{e}}^{-\mathrm{i}\omega t}.\end{array}$$

(3) 逆变换 由移位定理知

$$\begin{array}{}\text{(15.103a)}& \mathcal{F}\{f\left(ax+b\right)\}=1/a\cdot {\mathrm{e}}^{\mathrm{i}b\omega /a}F\left(\omega /a\right),\end{array}$$

对等式两侧作逆变换可得

$$\begin{array}{}\text{(15.103b)}& {\mathcal{F}}^{-1}\left\{{\mathrm{e}}^{\mathrm{i}\omega t}F\left(\omega \right)\right\}=f\left(x+t\right),{\mathcal{F}}^{-1}\left\{{\mathrm{e}}^{-\mathrm{i}\omega t}F\left(\omega \right)\right\}=f\left(x-t\right).\end{array}$$

运用积分法则

$$\begin{array}{}\text{(15.103c)}& \mathcal{F}\left\{{\int }_{-\mathrm{\infty }}^{x}f\left(\tau \right)\mathrm{d}\tau \right\}=\frac{1}{\mathrm{i}\omega }F\left(\omega \right)\end{array}$$

给出

$${\mathcal{F}}^{-1}\left\{\frac{1}{\mathrm{i}\omega }G\left(\omega \right){\mathrm{e}}^{\mathrm{i}\omega t}\right\}={\int }_{-\mathrm{\infty }}^x{\mathcal{F}}^{-1}\left\{G\left(\omega \right){\mathrm{e}}^{\mathrm{i}\omega t}\right\}\mathrm{d}\tau$$$$\begin{array}{}\text{(15.103d)}& ={\int }_{-\mathrm{\infty }}^{x}g\left(\tau +t\right)\mathrm{d}\tau ={\int }_{-\mathrm{\infty }}^{x+t}g\left(z\right)\mathrm{d}z,\end{array}$$

其中进行了替换 $\tau +t=z$ . 与以前的积分类似,有

$$\begin{array}{}\text{(15.103e)}& {\mathcal{F}}^{-1}\left\{-\frac{1}{\mathrm{i}\omega }G\left(\omega \right){\mathrm{e}}^{-\mathrm{i}\omega t}\right\}=-{\int }_{-\mathrm{\infty }}^{x-t}g\left(z\right)\mathrm{d}z.\end{array}$$

最后, 在原始空间内的解是

$$\begin{array}{}\text{(15.104)}& u\left(x,t\right)=\frac{1}{2}f\left(x+t\right)+\frac{1}{2}f\left(x-t\right)+{\int }_{x-t}^{x+t}g\left(z\right)\mathrm{d}z.\end{array}$$