Appearance
5.3.4 群表示
5.3.4.1 定义
1. 表示
群
向量空间
线性变换
这个变换也可以看作基的变换
于是群的每个元素被指派一个表示矩阵
表示矩阵与基的选取有关.
设等边三角形
旋转(5.98c)满足关系式
它们形成循环群
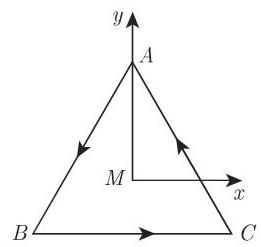
如果
给出群
对于表示矩阵(5.98f)和(5.98g),有与群元素
对于反射有
乘积
因此
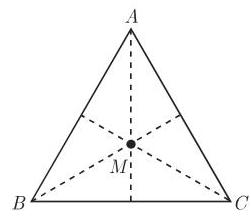
循环群
在反射
给出. 表示反射
(5.99f)
(5.99g)
矩阵(5.98f)和(5.98g)以及矩阵(5.99f)和(5.99g)一起形成二面角群
2. 忠实表示
一个表示称为忠实的,如果
3. 表示的性质
具有表示矩阵
5.3.4.2 特殊表示
1. 恒等表示
任何群
2. 伴随表示
称表示
3. 酉表示
对于酉表示, 所有的矩阵都是酉矩阵:
其中
4. 等价表示
两个表示
其中
有限群的任何表示等价于酉表示.
5. 群元素的特征
在表示
单位元
在原子或核物理学的壳层模型中,空间坐标为
其中, 当实施置换时, 依据第 452 页 5.3.3.1, 2., 它们中一个变换为另一个. 这样我们对于函数
总起来我们求得
对于特征, 我们有
5.3.4.3 表示的直和
可以通过形成表示矩阵的直和由维数为
表示矩阵的分块对角形蕴涵表示空间
表示 (5.107) 的特征是单个表示的特征之和:
5.3.4.4 表示的直积
如果
形成
两个表示的克罗内克积的特征等于因子的特征之积:
5.3.4.5 可约和不可约表示
如果表示空间
将表示矩阵分解.
如果
那么对于每个
这样的表示称为完全可约的.
注 对于群论在自然科学中的应用, 一个基本任务是将给定群的所有不等价的不可约表示分类.
在 (5.106c) 中给出的对称群
其中
5.3.4.6 第一舒尔 (Schur) 引理
如果
5.3.4.7 克勒布施-戈丹 (Clebsch-Gordan) 级数
一般地,两个不可约表示
级数:
其中
积空间中使得克罗内克积归约为它的不可约分量的基变换的矩阵元素称为克勒布施-戈丹系数.
5.3.4.8 对称群
1. 对称群
对称群
(5.119)
的整数分解来刻画. 通过安排方盒为杨氏 (Young) 图可得到这个分拆的图形表示. 对于群
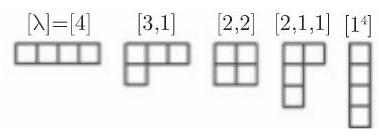
表示
给出.
通过交换行和列可构造与
在全同粒子系统的量子力学中泡利原理要求构造多体波函数, 使得对于任意两个粒子的所有坐标的交换是反对称的. 通常, 波函数是作为一个空间坐标函数与一个旋子变量函数的积的形式给出的. 如果这种情形由于粒子置换波函数的空间部分依据对称群的不可约表示