11.2.4 第二类弗雷德霍姆积分方程的数值解法

对于一个第二类弗雷德霍姆积分方程

$$\begin{array}{}\text{(11.23)}& \phi \left(x\right)=f\left(x\right)+\lambda {\int }_a^{b}K\left(x,y\right)\phi \left(y\right)\mathrm{d}y,\end{array}$$

为了获得其精确解, 用第 817 页的 11.2.1, 第 821 页的 11.2.2, 以及用第 823 页的 11.2.3 中给出的解法, 经常是不可能的, 或者要做太多的工作. 在一些这样的情形中, 为了近似可以用某些数值方法. 下面给出 3 种不同的方法来得到形如 (11.23) 积分方程的数值解.

11.2.4.1 积分的近似

1. 半离散问题

在研究积分方程 (11.23) 时, 经常用一个近似公式来代替其中的积分. 这些近似公式被称为求积公式(quadrature formulas). 它们有形式

$$\begin{array}{}\text{(11.24)}& {\int }_a^{b}f\left(x\right)\mathrm{d}x\approx Q_{[a,b]}\left(f\right)=\sum _{k=1}^n{\omega }_{k}f\left(x_k\right),\end{array}$$

即,代替积分,现在用被积函数在插值节点 $x_k$ 处赋以权值 ${\omega }_k$ 的代换值之和. 诸数 ${\omega }_k$ 要被适当地选取 (以便与 $f$ 无关). 用近似形式,方程 (11.23) 可以被写成

$$\begin{array}{}\text{(11.25a)}& \phi \left(x\right)\approx f\left(x\right)+\lambda Q_{[a,b]}\left(K\left(x,\cdot \right)\phi (\cdot )\right)=f\left(x\right)+\lambda \sum _{k=1}^n{\omega }_{k}K\left(x,y_k\right)\phi \left(y_k\right).\end{array}$$

求积公式 $Q_{[a,b]}\left(K\left(x,\cdot \right)\phi (\cdot )\right)$ 还依赖于变量 $x$ . 在函数变量位置上的点意味着求积公式是关于变量 $y$ 所用的. 定义关系式

$$\begin{array}{}\text{(11.25b)}& \overline{\phi }\left(x\right)=f\left(x\right)+\lambda \sum _{k=1}^n{\omega }_{k}K\left(x,y_k\right)\overline{\phi }\left(y_k\right).\end{array}$$

$\overline{\phi }\left(x\right)$ 是精确解 $\phi \left(x\right)$ 的一个近似. 把 (11.25b) 视为一个半离散问题(semi-discrete problem),因为变量 $y$ 被转为离散值,而变量 $x$ 仍可为任意的.

如果方程 (11.25b) 对一个函数 $\overline{\phi }\left(x\right)$ 在每个点 $x\in \left[a,b\right]$ 处成立,那么它必定在每个插值节点 $x=x_k$ 处成立:

$$\begin{array}{}\text{(11.25c)}& \overline{\phi }\left(x_k\right)=f\left(x_k\right)+\lambda \sum _{j=1}^n{\omega }_{j}K\left(x_k,y_j\right)\overline{\phi }\left(y_j\right),k=1,2,\cdots ,n.\end{array}$$

这是一个关于 $n$ 个未知值 $\overline{\phi }\left(x_k\right)$ 的 $n$ 个方程的一个线性方程组. 把这些解代入(11.25b), 产生了半离散问题的解. 这个方法的精度和计算量依赖于所用的求积公式. 例如,用左矩形公式(参见第 1253 页 19.3.2.1) 以及等距划分 $y_k=x_k=$ $a+h\left(k-1\right),h=\left(b-a\right)/n\left(k=1,\cdots ,n\right)$ ,产生

$$\begin{array}{}\text{(11.26a)}& {\int }_a^{b}K\left(x,y\right)\overline{\phi }\left(y\right)\mathrm{d}y\approx \sum _{k=1}^{n}hK\left(x,y_k\right)\overline{\phi }\left(y_k\right).\end{array}$$

利用记号

$$\begin{array}{}\text{(11.26b)}& K_{jk}=K\left(x_j,y_k\right),f_k=f\left(x_k\right),{\phi }_k=\overline{\phi }\left(x_k\right),\end{array}$$

方程组(11.25c)有形式:

$$\left(1-\lambda h{K}_{11}\right){\phi }_1-\lambda h{K}_{12}{\phi }_2-\cdots -\lambda h{K}_{1n}{\phi }_n=f_1,$$$$\begin{array}{}\text{(11.26c)}& -\lambda h{K}_{21}{\phi }_1+\left(1-\lambda h{K}_{22}\right){\phi }_2-\cdots -\lambda h{K}_{2n}{\phi }_n=f_2,\end{array}$$$$-\lambda h{K}_{n1}{\phi }_1-\lambda h{K}_{n2}{\phi }_2-\cdots +\left(1-\lambda h{K}_{nn}\right){\phi }_n=f_n.$$

相同的方程组被包含在弗雷德霍姆解法 (参见第 823 页 11.2.3) 中. 因为矩形公式并非足够精确, 因此为了更好地近似积分, 可以增加插值节点的数目, 但随之而来的是方程组维数的增加. 因而要寻找另外的求积公式.

2. 尼斯特伦法

在所谓的尼斯特伦法(Nyström method) 中, 高斯求积公式被用于求积分的近似 (参见第 1254 页 19.3.3,3.). 为了推导它, 考虑积分

$$\begin{array}{}\text{(11.27a)}& I={\int }_a^{b}f\left(x\right)\mathrm{d}x.\end{array}$$

用一个多项式 $p\left(x\right)$ ,即 $f\left(x\right)$ 在插值节点 $x_k$ 处的插值多项式来代替被积函数:

$$p\left(x\right)=\sum _{k=1}^n{L}_k\left(x\right)f\left(x_k\right),$$

其中

$$\begin{array}{}\text{(11.27b)}& L_k\left(x\right)=\frac{\left(x-x_1\right)\cdots \left(x-x_{k-1}\right)\left(x-x_{k+1}\right)\cdots \left(x-x_n\right)}{\left(x_k-x_1\right)\cdots \left(x_k-x_{k-1}\right)\left(x_k-x_{k+1}\right)\cdots \left(x_k-x_n\right)}.\end{array}$$

对于这个多项式, 有

$$\begin{array}{}\text{(11.27c)}& p\left(x_k\right)=f\left(x_k\right),k=1,\cdots ,n.\end{array}$$

用 $p\left(x\right)$ 代替被积函数 $f\left(x\right)$ 导致求积公式

$$\begin{array}{}\text{(11.27d)}& {\int }_a^{b}f\left(x\right)\mathrm{d}x\approx {\int }_a^{b}p\left(x\right)\mathrm{d}x=\sum _{k=1}^{n}f\left(x_k\right){\int }_a^b{L}_k\left(x\right)\mathrm{d}x=\sum _{k=1}^n{\omega }_{k}f\left(x_k\right),\end{array}$$

其中 ${\omega }_k={\int }_a^b{L}_k\left(x\right)\mathrm{d}x$ . 对于高斯求积公式,不能任意选取插值节点,它们必须用

公式

$$\begin{array}{}\text{(11.28a)}& x_k=\frac{a+b}{2}+\frac{b-a}{2}{t}_k,k=1,2,\cdots ,n\end{array}$$

来选取. 这 $n$ 个 $t_k$ 值是第一类勒让德多项式 (参见第 748 页 9.1.2.6,3.)

$$\begin{array}{}\text{(11.28b)}& P_n\left(t\right)=\frac{1}{2^n\cdot n!}\frac{d^n\left[{(t^2-1)}^n\right]}{d{t}^n}\end{array}$$

的 $n$ 个根. 这些根都在区间 $\left[-1,+1\right]$ 中. 由代换 $x-x_k=\frac{b-a}{2}\left(t-t_k\right)$ 可以计算诸系数 ${\omega }_k$ ,因而:

$${\omega }_k={\int }_a^b{L}_k\left(x\right)\mathrm{d}x=\left(b-a\right)\frac{1}{2}{\int }_{-1}^1\frac{\left(t-t_1\right)\cdots \left(t-t_{k-1}\right)\left(t-t_{k+1}\right)\cdots \left(t-t_n\right)}{\left(t_k-t_1\right)\cdots \left(t_k-t_{k-1}\right)\left(t_k-t_{k+1}\right)\cdots \left(t_k-t_n\right)}\mathrm{d}t$$$$\begin{array}{}\text{(11.29)}& =\left(b-a\right)A_k\text{.}\end{array}$$

在表 11.1 中给出了第一类勒让德多项式的根和 $n=1,\cdots ,6$ 的诸权值 $A_k$ .

$◼$ 用尼斯特伦法对于 $n=3$ 解积分方程 $\phi \left(x\right)=\cos \pi x+\frac{x}{x^2+{\pi }^2}\left({\mathrm{e}}^x+1\right)+$${\int }_0^1{\mathrm{e}}^{xy}\phi \left(y\right)\mathrm{d}y$

$$n=3:x_1=0.1127,$$$$x_2=0.5,$$$$x_3=0.8873,$$$$A_1=0.2778,$$$$A_2=0.4444\text{,}$$$$A_3=0.2778\text{,}$$$$f_1=0.96214,$$$$f_2=0.13087,$$$$f_3=-0.65251\text{,}$$$$K_{11}=1.01278,$$$$K_{22}=1.28403,$$

$K_{33}=2.19746,$

$$K_{12}=K_{21}=1.05797,$$$$K_{13}=K_{31}=1.10517,$$

$K_{23}=K_{32}=1.55838.$对于 ${\phi }_1,{\phi }_2$ 和 ${\phi }_3$ 的方程组(11.25c)是

$$0.71864{\phi }_1-0.47016{\phi }_2-0.30702{\phi }_3=0.96214,$$$$-0.29390{\phi }_1+0.42938{\phi }_2-0.43292{\phi }_3=0.13087,$$$$-0.30702{\phi }_1-0.69254{\phi }_2+0.38955{\phi }_3=-0.65251.$$

$n$	$t$	$A$	$n$	$t$	$A$
1	$t_1=0$	$A_1=1$	5	$t_1=-0.9062$	$A_1=0.1185$
2	$t_1=-0.5774$	$A_1=0.5$		$t_2=-0.5384$	$A_2=0.2393$
	$t_2=0.5774$	$A_2=0.5$		$t_3=0$	$A_3=0.2844$
3	$t_1=-0.7746$	$A_1=0.2778$		$t_4=0.5384$	$A_4=0.2393$
	$t_2=0$	$A_2=0.4444$		$t_5=0.9062$	$A_5=0.1185$
	$t_3=0.7746$	$A_3=0.2778$	6	$t_1=-0.9324$	$A_1=0.0857$
4	$t_1=-0.8612$	$A_1=0.1739$		$t_2=-0.6612$	$A_2=0.1804$
	$t_2=-0.3400$	$A_2=0.3261$		$t_3=-0.2386$	$A_3=0.2340$
	$t_3=0.3400$	$A_3=0.3261$		$t_4=0.2386$	$A_4=0.2340$
	$t_4=0.8612$	$A_4=0.1739$		$t_5=0.6612$	$A_5=0.1804$
				$t_6=0.9324$	$A_6=0.0857$

这方程组的解是 ${\phi }_1=0.93651,{\phi }_2=-0.00144,{\phi }_3=-0.93950$ . 精确解在插值节点处的代换值是: $\phi \left(x_1\right)=0.93797,\phi \left(x_2\right)=0,\phi \left(x_3\right)=-0.93797$ .

11.2.4.2 核近似

用一个核 $\overline{K}\left(x,y\right)$ 代替核 $K\left(x,y\right)$ ,使得对于 $a\le x\le b,a\le y\le b$ 有 $\overline{K}\left(x,y\right)\approx$ $K\left(x,y\right)$ . 试图选取一个核,使得最容易获得积分方程

$$\begin{array}{}\text{(11.30)}& \overline{\phi }\left(x\right)=f\left(x\right)+\lambda {\int }_a^b\overline{K}\left(x,y\right)\overline{\phi }\left(y\right)\mathrm{d}y\end{array}$$

的解.

1. 张量积近似

经常用到的核的近似是形如

$$\begin{array}{}\text{(11.31a)}& K\left(x,y\right)\approx \overline{K}\left(x,y\right)=\sum _{j=0}^n\sum _{k=0}^n{d}_{jk}{\alpha }_j\left(x\right){\beta }_k\left(y\right)\end{array}$$

的张量积近似(tensor product approximation),其中 ${\alpha }_0\left(x\right),\cdots ,{\alpha }_n\left(x\right)$ 和 ${\beta }_0\left(y\right)$ , $\cdots ,{\beta }_n\left(y\right)$ 是给定的线性无关的函数,它们的系数 $d_{jk}$ 必须选取得使二重和在某种意义下充分地逼近核. 用一个退化核重写 ${\left(11.31\mathrm{a}\right)}^{\mathrm{T}}$ :

$$\begin{array}{}\text{(11.31b)}& \overline{K}\left(x,y\right)=\sum _{j=0}^n{\alpha }_j\left(x\right)\left[\sum _{k=0}^n{d}_{jk}{\beta }_k\left(y\right)\right],{\delta }_j\left(y\right)=\sum _{k=0}^n{d}_{jk}{\beta }_k\left(y\right),\end{array}$$$$\overline{K}\left(x,y\right)=\sum _{j=0}^n{\alpha }_j\left(x\right){\delta }_j\left(y\right).$$

现在, 可以把第 817 页 11.2.1 的解法用于积分方程

$$\begin{array}{}\text{(11.31c)}& \overline{\phi }\left(x\right)=f\left(x\right)+\lambda {\int }_a^b\left[\sum _{j=0}^n{\alpha }_j\left(x\right){\delta }_j\left(y\right)\right]\overline{\phi }\left(y\right)\mathrm{d}y.\end{array}$$

应该选取诸函数 ${\alpha }_0\left(x\right),\cdots ,{\alpha }_n\left(x\right)$ 和 ${\beta }_0\left(y\right),\cdots ,{\beta }_n\left(y\right)$ ,使得可以容易地计算 (11.31a) 中的系数 $d_{jk}$ ,并且也使得计算 (11.31c) 的解不太困难.

---

① 原文把 (11.31b) 后两等式连在一起了: ${\delta }_j\left(y\right)=\sum _{k=0}^n{d}_{jk}{\beta }_k\left(y\right)\overline{K}\left(x,y\right)=$ $\sum _{j=0}^n{\alpha }_j\left(x\right){\delta }_j\left(y\right)$ . 一译者注

---

2. 特殊样条函数法

为了在积分区间 $\left[a,b\right]=\left[0,1\right]$ 上逼近一个特殊核,选取

$$\begin{array}{}\text{(11.32)}& {\alpha }_k\left(x\right)={\beta }_k\left(x\right)=\{\begin{array}{ll}1-n\left|x-\frac{k}{n}\right|,& \frac{k-1}{n}\le x\le \frac{k+1}{n},\\ 0,& \text{ 其他情形. }\end{array}\end{array}$$

函数 ${\alpha }_k\left(x\right)$ 仅在所谓的承载区间(carrier interval) $\left(\frac{k-1}{n},\frac{k+1}{n}\right)$ 上有非零值 (图 11.1).

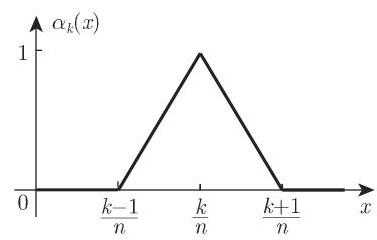
为了计算 (11.31a) 中的系数 $d_{jk}$ ,在点 $x=l/n,y=i/n\left(l,i=0,1,\cdots ,n\right)$ 处考虑 $\overline{K}\left(x,y\right)$ . 则成立

$$\begin{array}{}\text{(11.33)}& {\alpha }_j\left(\frac{l}{n}\right){\alpha }_k\left(\frac{i}{n}\right)=\{\begin{array}{ll}1,& j=l,k=i,\\ 0,& \text{ 其他情形,}\end{array}\end{array}$$

所以 $\overline{K}\left(l/n,i/n\right)=d_{li}$ . 因而有代换 $d_{li}=\overline{K}\left(\frac{l}{n},\frac{i}{n}\right)=K\left(\frac{l}{n},\frac{i}{n}\right)$ . 现在 (11.31a) 有形式

$$\begin{array}{}\text{(11.34)}& \overline{K}\left(x,y\right)=\sum _{j=0}^n\sum _{k=0}^{n}K\left(\frac{j}{n},\frac{k}{n}\right){\alpha }_j\left(x\right){\beta }_k\left(y\right).\end{array}$$

如所知道的, (11.31c) 的解有形式

$$\begin{array}{}\text{(11.35)}& \overline{\phi }\left(x\right)=f\left(x\right)+A_0{\alpha }_0\left(x\right)+\cdots +A_n{\alpha }_n\left(x\right).\end{array}$$

表达式 $A_0{\alpha }_0\left(x\right)+\cdots +A_n{\alpha }_n\left(x\right)$ 是一个分段线性函数,它在点 $x_k=k/n$ 处取替换值 $A_k$ . 用对于退化核给出的方法解 (11.31c),得到关于数 $A_0,\cdots ,A_n$ 的一个线性方程组:

$$\left(1-\lambda c_{00}\right)A_0-\lambda c_{01}{A}_1-\cdots -\lambda c_{0n}{A}_n=b_0,$$$$\begin{array}{}\text{(11.36a)}& -\lambda c_{10}{A}_0+\left(1-\lambda c_{11}\right)A_1-\cdots -\lambda c_{1n}{A}_n=b_1,\end{array}$$

......

$$-\lambda c_{n0}{A}_0-\lambda c_{n1}{A}_1-\cdots +\left(1-\lambda c_{nn}\right)A_n=b_n.$$

其中

$$c_{jk}={\int }_0^1{\delta }_j\left(x\right){\alpha }_k\left(x\right)\mathrm{d}x={\int }_0^1\left[\sum _{i=0}^{n}K\left(\frac{j}{n},\frac{i}{n}\right){\alpha }_j\left(x\right)\right]{\alpha }_k\left(x\right)\mathrm{d}x$$$$=K\left(\frac{j}{n},\frac{0}{n}\right){\int }_0^1{\alpha }_0\left(x\right){\alpha }_k\left(x\right)\mathrm{d}x$$$$\begin{array}{}\text{(11.36b)}& +\cdots +K\left(\frac{j}{n},\frac{n}{n}\right){\int }_0^1{\alpha }_n\left(x\right){\alpha }_k\left(x\right)\mathrm{d}x.\end{array}$$

对于这些积分, 有

$$\begin{array}{}\text{(11.36c)}& I_{jk}={\int }_0^1{\alpha }_j\left(x\right){\alpha }_k\left(x\right)\mathrm{d}x=\{\begin{array}{ll}\frac{1}{3n},& j=0,k=0\text{ 和 }j=n,k=n,\\ \frac{2}{3n},& j=k,1\le j\le n,\\ \frac{1}{6n},& j=k+1,j=k-1,\\ 0,& \text{ 其他情形. }\end{array}\end{array}$$

(11.36a) 中的数 $b_k$ 由

$$\begin{array}{}\text{(11.36d)}& b_k={\int }_0^{1}f\left(x\right)\left[\sum _{j=0}^{n}K\left(\frac{k}{n},\frac{j}{n}\right){\alpha }_j\left(x\right)\right]\mathrm{d}x\end{array}$$

给出. 分别用 (11.36a) 中的数 $c_{jk}$ 组成矩阵 $\mathbf{C}$ ,用值 $K\left(j/n,k/n\right)$ 组成矩阵 $\mathbf{B}$ ,用值 $I_{jk}$ 组成矩阵 $\mathbf{A}$ ,数 $b_0,\cdots ,b_n$ 组成向量 $\underset{―}{\mathbf{b}}$ ,数 $A_0,\cdots ,A_n$ 组成向量 $\underset{―}{\mathbf{a}}$ ,则方程组 (11.36a) 有形式

$$\begin{array}{}\text{(11.36e)}& \left(\mathbf{I}-\lambda \mathbf{C}\right)\underset{―}{\mathbf{a}}=\left(\mathbf{I}-\lambda \mathbf{B}\mathbf{A}\right)\underset{―}{\mathbf{a}}=\underset{―}{\mathbf{b}}.\end{array}$$

在此情形,若矩阵 $\left(\mathbf{I}-\lambda \mathbf{BA}\right)$ 是正规的时,这个方程组有一个唯一解 $\underset{―}{\mathbf{a}}=\left(A_0,\cdots ,A_n\right)$ .

11.2.4.3 配置法

假设在区间 $\left[a,b\right]$ 中 $n$ 个函数 ${\phi }_1\left(x\right),\cdots ,{\phi }_n\left(x\right)$ 是线性无关的. 它们可以被用来构成解 $\phi \left(x\right)$ 的一个近似函数 $\overline{\phi }\left(x\right)$ :

$$\begin{array}{}\text{(11.37a)}& \phi \left(x\right)\approx \overline{\phi }\left(x\right)=a_1{\phi }_1\left(x\right)+a_2{\phi }_2\left(x\right)+\cdots +a_n{\phi }_n\left(x\right).\end{array}$$

现在的问题是确定系数 $a_1,\cdots ,a_n$ . 通常,不存在 $a_1,\cdots ,a_n$ ,使得以这种形式给出的函数 $\overline{\phi }\left(x\right)$ 表示积分方程 (11.23) 的精确解 $\phi \left(x\right)=\overline{\phi }\left(x\right)$ . 因而,在积分区间中界定 $n$ 个插值点 $x_1,\cdots ,x_n$ ,使得近似函数 (11.37a) 至少在这些点上满足积分方程:

$$\begin{array}{}\text{(11.37b)}& \overline{\phi }\left(x_k\right)=a_1{\phi }_1\left(x_k\right)+\cdots +a_n{\phi }_n\left(x_k\right)\end{array}$$$$=f\left(x_k\right)+\lambda {\int }_a^{b}K\left(x_k,y\right)\left[a_1{\phi }_1\left(y\right)+\cdots +a_n{\phi }_n\left(y\right)\right]\mathrm{d}y\left(k=1,\cdots ,n\right).\left(11.37\mathrm{c}\right)$$

在一些变换下, 这个方程组取下述形式:

$$\left[{\phi }_1\left(x_k\right)-\lambda {\int }_a^{b}K\left(x_k,y\right){\phi }_1\left(y\right)\mathrm{d}y\right]a_1+\cdots +\left[{\phi }_n\left(x_k\right)-\lambda {\int }_a^{b}K\left(x_k,y\right){\phi }_n\left(y\right)\mathrm{d}y\right]a_n$$$$\begin{array}{}\text{(11.37d)}& =f\left(x_k\right)\left(k=1,\cdots ,n\right).\end{array}$$

定义矩阵

$$\begin{array}{}\text{(11.37e)}& \mathbf{A}=\left(\begin{array}{ccc}{\phi }_1\left(x_1\right)& \cdots & {\phi }_n\left(x_1\right)\\ ⋮& & ⋮\\ {\phi }_1\left(x_n\right)& \cdots & {\phi }_n\left(x_n\right)\end{array}\right),\mathbf{B}=\left(\begin{array}{ccc}{\beta }_{11}& \cdots & {\beta }_{1n}\\ ⋮& & ⋮\\ {\beta }_{n1}& \cdots & {\beta }_{nn}\end{array}\right),\end{array}$$

其中 ${\beta }_{jk}={\int }_a^{b}K\left(x_j,y\right){\phi }_k\left(y\right)\mathrm{d}y$ ,并定义向量

$$\begin{array}{}\text{(11.37f)}& \underset{―}{\mathbf{a}}={(a_1,\cdots ,a_n)}^{\mathrm{T}},\underset{―}{\mathbf{b}}={(f\left(x_1\right),\cdots ,f\left(x_n\right))}^{\mathrm{T}},\end{array}$$

则确定数 $a_1,\cdots ,a_n$ 的方程组可以被写成矩阵形式:

$$\begin{array}{}\text{(11.37g)}& \left(\mathbf{A}-\lambda \mathbf{B}\right)\underset{―}{\mathbf{a}}=\underset{―}{\mathbf{b}}.\end{array}$$

$◼\phi \left(x\right)=\frac{\sqrt{x}}{2}+{\int }_0^1\sqrt{xy}\phi \left(y\right)\mathrm{d}y$ . 近似函数为 $\overline{\phi }\left(x\right)=a_1{x}^2+a_{2}x+a_3,{\phi }_1\left(x\right)=$ $x^2,{\phi }_2\left(x\right)=x,{\phi }_3\left(x\right)=1$ . 插值节点为 $x_1=0,x_2=0.5,x_3=1$ .

$$\mathbf{A}=\left(\begin{array}{ccc}0& 0& 1\\ \frac{1}{4}& \frac{1}{2}& 1\\ 1& 1& 1\end{array}\right),\mathbf{B}=\left(\begin{array}{ccc}0& 0& 0\\ \frac{\sqrt{2}}{7}& \frac{\sqrt{2}}{5}& \frac{\sqrt{2}}{3}\\ \frac{2}{7}& \frac{2}{5}& \frac{2}{3}\end{array}\right),\underset{―}{\mathbf{b}}=\left(\begin{array}{c}0\\ \frac{1}{2\sqrt{2}}\\ \frac{1}{2}\\ \frac{1}{2}\end{array}\right).$$

方程组为

$$a_3=0,$$$$\left(\frac{1}{4}-\frac{\sqrt{2}}{7}\right)a_1+\left(\frac{1}{2}-\frac{\sqrt{2}}{5}\right)a_2+\left(1-\frac{\sqrt{2}}{3}\right)a_3=\frac{1}{2\sqrt{2}},$$$$\frac{5}{7}{a}_1+\frac{3}{5}{a}_2+\frac{1}{3}{a}_3=\frac{1}{2}$$

它的解为 $a_1=-0.8197,a_2=1.8092,a_3=0$ ,因此由这些值得 $\overline{\phi }\left(x\right)=-0.8197x^2+$ $1.8092x$ ,因而 $\overline{\phi }\left(0\right)=0,\overline{\phi }\left(0.5\right)=0.6997,\overline{\phi }\left(1\right)=0.9895$ .

积分方程的精确解是 $\phi \left(x\right)=\sqrt{x}$ ,因而 $\phi \left(0\right)=0,\phi \left(0.5\right)=0.7070,\phi \left(1\right)=1$ .

为了改进此例中的精度, 增加多项式的次数并非一个好主意, 因为较高次的多项式在数值上是不稳定的. 利用不同的样条函数要好得多, 例如, 一个分段线性逼近 $\overline{\phi }\left(x\right)=a_1{\phi }_1\left(x\right)+a_2{\phi }_2\left(x\right)+\cdots +a_n{\phi }_n\left(x\right)$ ,这里的函数是在 11.2.4.2 节中引进

的:

$${\phi }_k\left(x\right)=\{\begin{array}{ll}1-n\left|x-\frac{k}{n}\right|,& \frac{k-1}{n}\le x\le \frac{k+1}{n},\\ 0,& \text{ 其他情形. }\end{array}$$

在这个情形,解 $\phi \left(x\right)$ 被一个折线函数 $\overline{\phi }\left(x\right)$ 所近似.

注 就配置法插值节点的选取而论, 并不存在理论约束. 然而在此情形, 如果解函数在某个子区间中极为振荡时, 必须在这个区间中增加插值节点的数目.