8.5.1 第一类曲面积分

第一类线积分是普通积分的推广 (参见第 684 页 8.3.1), 与之相同, 曲面积分或空间曲面积分是二重积分的推广.

8.5.1.1 第一类曲面积分的概念

1. 定义

设有一定义在连通区域上的三元函数 $u=f\left(x,y,z\right),S$ 为曲面上的一个区域, 则函数在 $S$ 上的第一类曲面积分为

$$\begin{array}{}\text{(8.148a)}& {\int }_{S}f\left(x,y,z\right)\mathrm{d}S\end{array}$$

第一类曲面积分的数值可按如下方法来定义 (参见图 8.44):

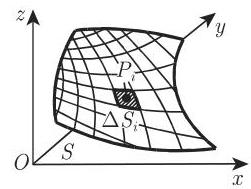
(1) 把区域 $S$ 任意分成 $n$ 个小区域 $\mathrm{\Delta }{S}_i$ .

(2) 在小区域 $\mathrm{\Delta }{S}_i$ 的内部或边界任取一点 $P_i\left(x_i,y_i,z_i\right)$ .

(3) 用点 $P_i\left(x_i,y_i,z_i\right)$ 处的函数值 $f\left(x_i,y_i,z_i\right)$ 乘以相应小区域的面积 $\mathrm{\Delta }{S}_i$ .

(4) 将所有乘积 $f\left(x_i,y_i,z_i\right)\mathrm{\Delta }{S}_i$ 作和.

(5) 当每个小区域的直径都趋于 0,即 $\mathrm{\Delta }{S}_i\to 0,n\to \mathrm{\infty }$ 时,确定和式

$$\begin{array}{}\text{(8.148b)}& \sum _{i=1}^{n}f\left(x_i,y_i,z_i\right)\mathrm{\Delta }{S}_i\end{array}$$

的极限 (参见第 694 页 8.4.1.1, 1.).

若无论区域 $S$ 的分法如何,也不论点 $P_i\left(x_i,y_i,z_i\right)$ 的取法如何,上述极限都存在,则称之为函数 $u=f\left(x,y,z\right)$ 在曲面 $S$ 上的第一类曲面积分,记作

$$\begin{array}{}\text{(8.148c)}& {\int }_{S}f\left(x,y,z\right)\mathrm{d}S=\underset{\begin{array}{c}\mathrm{\Delta }{S}_i\to 0\\ n\to \mathrm{\infty }\end{array}}{lim}\sum _{i=1}^{n}f\left(x_i,y_i,z_i\right)\mathrm{\Delta }{S}_i.\end{array}$$

2. 存在定理

若函数 $u=f\left(x,y,z\right)$ 在某区域上连续,且定义曲面的函数有连续导数,则第一类曲面积分存在.

8.5.1.2 第一类曲面积分的计算

第一类曲面积分的计算可化成平面区域上二重积分的计算 (参见第 694 页 8.4.1).

1. 曲面的显函数表示

设曲面方程的显形式方程为

$$\begin{array}{}\text{(8.149)}& z=z\left(x,y\right)\end{array}$$

则

$$\begin{array}{}\text{(8.150a)}& {\int }_{S}f\left(x,y,z\right)\mathrm{d}S={\iint }_{S^{\prime }}f\left[x,y,z\left(x,y\right)\right]\sqrt{1+p^2+q^2}\mathrm{d}x\mathrm{d}y,\end{array}$$

其中 $S^{\prime }$ 为 $S$ 在 $xOy$ 面的投影, $p=\frac{\partial z}{\partial x},q=\frac{\partial z}{\partial y}$ . 此处假设曲面 $S$ 中的每个点都对应 $xOy$ 面内 $S^{\prime }$ 中的唯一一点,即曲面中的点由它们的坐标唯一确定. 若这一条不成立,可以把 $S$ 分成几部分,使得每部分都满足该条件. 由此在整个曲面的积分可以表示成 $S$ 的各个部分积分的代数和.

因为曲面 (8.149) 的法线方程形如 $\frac{X-x}{p}=\frac{Y-y}{q}=\frac{Z-z}{-1}$ (参见第 353 页表 3.29),法线方向与 $z$ 轴夹角的余弦 $\cos \gamma =\frac{1}{\sqrt{1+p^2+q^2}}$ ,故方程 (8.150a) 可以写成

$$\begin{array}{}\text{(8.150b)}& {\int }_{S}f\left(x,y,z\right)\mathrm{d}S={\iint }_{S_{xy}}f\left[x,y,z\left(x,y\right)\right]\frac{\mathrm{d}{S}_{xy}}{\cos \gamma }.\end{array}$$

在计算第一类曲面积分时,总把角 $\gamma$ 看成锐角,故恒有 $\cos \gamma >0$ .

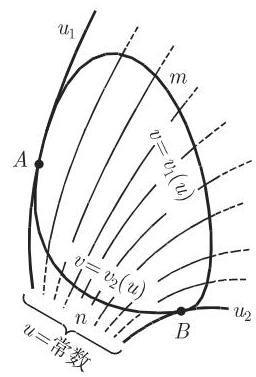
2. 曲面的参数表示

若曲面 $S$ 以参数方程的形式给出 (图 8.45)

$$\begin{array}{}\text{(8.151a)}& x=x\left(u,v\right),y=y\left(u,v\right),z=z\left(u,v\right),\end{array}$$

则

$${\int }_{S}f\left(x,y,z\right)\mathrm{d}S$$$$\begin{array}{}\text{(8.151b)}& ={\iint }_{\mathrm{\Delta }}f\left[x\left(u,v\right),y\left(u,v\right),z\left(u,v\right)\right]\sqrt{EG-F^2}\mathrm{d}u\mathrm{d}v,\end{array}$$

其中 $E,F,G$ 均为第 353 页 3.6.3.3,1. 给出的量,参数形式的区域面积微元为

$$\begin{array}{}\text{(8.151c)}& \sqrt{EG-F^2}\mathrm{d}u\mathrm{d}v=\mathrm{d}S,\end{array}$$

$\mathrm{\Delta }$ 是与给定的曲面区域相对应的关于参数 $u,v$ 的区域. 关于 $u,v$ 依次积分,可计算曲面积分

$${\int }_S\mathrm{\Phi }\left(u,v\right)\mathrm{d}S={\int }_{u_1}^{u_2}{\int }_{v_1\left(u\right)}^{v_2\left(u\right)}\mathrm{\Phi }\left(u,v\right)\sqrt{EG-F^2}\mathrm{d}v\mathrm{d}u,$$$$\begin{array}{}\text{(8.151d)}& \mathrm{\Phi }=f\left[x\left(u,v\right),y\left(u,v\right),z\left(u,v\right)\right],\end{array}$$

其中 $u_1,u_2$ 是包含区域 $S$ 的坐标线 $u=$ 常数的下限和上限坐标 (图 8.45), $v=$ $v_1\left(u\right),v=v_2\left(u\right)$ 是 $S$ 的边界曲线 $\stackrel{⏜}{AmB}$ 和 $\stackrel{⏜}{AnB}$ 的方程.

注 (8.150a) 是 (8.151b) 的特殊情况, 事实上,

$$\begin{array}{}\text{(8.152)}& u=x,v=y,E=1+p^2,F=pq,G=1+q^2.\end{array}$$

3. 曲面的面积微元

坐标	面积微元
笛卡儿坐标 $x,y,z=z\left(x,y\right)$	$\mathrm{d}S=\sqrt{1+{\left(\frac{\partial z}{\partial x}\right)}^2}+{\left(\frac{\partial z}{\partial y}\right)}^2\mathrm{d}x\mathrm{d}y$
柱面侧面, $R$ (常数,半径),坐标 $\phi ,z$	$\mathrm{d}S=R\mathrm{d}\phi \mathrm{d}z$
球面 $R$ (常数,半径),坐标 $\vartheta ,\phi$	$\mathrm{d}S=R^2\sin \vartheta \mathrm{d}\vartheta \mathrm{d}\phi$
任意曲线坐标 $u,v(E,F,G$ 参见 354 页弧微分)	$\mathrm{d}S=\sqrt{EG-F^2}\mathrm{d}u\mathrm{d}v$

8.5.1.3 第一类曲面积分的应用

1. 曲面的面积

$$\begin{array}{}\text{(8.153)}& S={\int }_S\mathrm{d}S\end{array}$$

2. 质地不均匀的曲面 $S$ 的质量

设密度 $\varrho =f\left(x,y,z\right)$ 依坐标变化,有

$$\begin{array}{}\text{(8.154)}& M_S={\int }_S\varrho \mathrm{d}S\end{array}$$