2.1.5 函数的连续性

2.1.5.1 连续与间断的概念

实际上大部分函数都是连续函数,也就是函数自变量变化很小时,连续函数 $y\left(x\right)$ 的变化也很小, 这样的函数图像为一条连续曲线. 如果曲线在某些点断开, 相应的函数就不是连续函数, 曲线断开的自变量的值称为间断点. 图 2.9 所示为分段连续曲线,间断点为 $A,B,C,D,E,F,G$ ,箭头表示端点不在曲线上.

2.1.5.2 连续的定义

函数 $y=f\left(x\right)$ 称为在点 $x=a$ 连续,若

(1) $f\left(x\right)$ 在 $a$ 点有定义;

(2) $\underset{x\to a}{lim}f\left(x\right)$ 存在且 $\underset{x\to a}{lim}f\left(x\right)=f\left(a\right)$ .

即对任意 $\epsilon >0$ ,存在 $\delta \left(\epsilon \right)>0$ ,使得当 $\left|x-a\right|<\delta$ 时,对一切 $x$ 有

$$\begin{array}{}\text{(2.30)}& \left|f\left(x\right)-f\left(a\right)\right|<\epsilon .\end{array}$$

若不管 $\underset{x\to a}{lim}f\left(x\right)=f\left(a\right)$ 与否,只考虑一侧的极限 $\underset{x\to a-0}{lim}f\left(x\right)($ 或 $\underset{x\to a+0}{lim}f\left(x\right))$ 且其等于 $f\left(a\right)$ ,则称为单侧 (左侧或右侧) 连续.

若函数在 $a$ 到 $b$ 区间内每一点连续,则称函数为该区间的连续函数,其中的区间可以为开区间、半开区间或闭区间 (参见第 3 页 1.1.1.3,3.). 若函数在数轴上的每一点都有定义且连续, 则称该函数为处处连续函数.

若函数在 $x=a$ 处无定义,或有定义但 $\underset{x\to a}{lim}f\left(x\right)\ne f\left(a\right)$ ,或极限不存在,则 $x=a$ 为函数的间断点,它可能是函数定义域的内点或端点.

若函数仅在 $x=a$ 的一侧有定义,如 $\sqrt{x}$ 仅在 $x=0$ 的一侧有定义, $\arccos x$ 仅在 $x=1$ 的一侧有定义,则它不是间断点,但是为终点.

若函数除在有限个有限跳跃间断点外, 在区间上的每一点都连续, 则称该函数为分段连续函数.

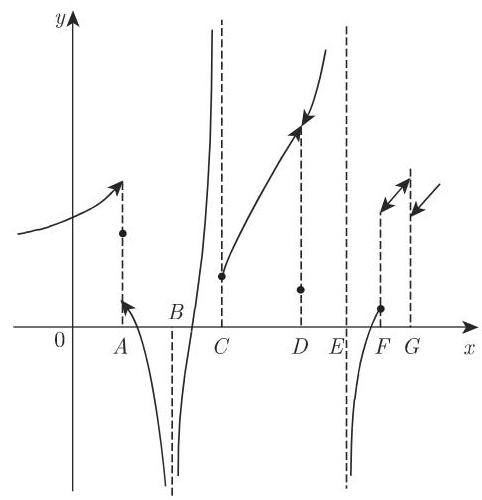
2.1.5.3 常见间断点的类型

1. 函数值趋近无穷

当函数趋于 $\pm \mathrm{\infty }$ 时,是最常见的间断点 (图 2.9 中的 $B,C,E$ ).

$◼\mathbf{A}$: $f\left(x\right)=\tan x,f\left(\frac{\pi }{2}-0\right)=+\mathrm{\infty },f\left(\frac{\pi }{2}+0\right)=-\mathrm{\infty }$ (参见第 99 页图 2.34), 图 2.9 中的点 $E$ 也是这种类型的间断点,符号 $f\left(a-0\right),f\left(a+0\right)$ 的意义参见第 70 页 2.1.4.5.

$◼\mathbf{B}$: $f\left(x\right)=\frac{1}{{(x-1)}^2},f\left(1-0\right)=+\mathrm{\infty },f\left(1+0\right)=+\mathrm{\infty }$ ,图 2.9 中的点 $B$ 是这种类型的间断点.

IC: $f\left(x\right)={\mathrm{e}}^{\frac{1}{x-1}},f\left(1-0\right)=0,f\left(1+0\right)=\mathrm{\infty }$ ,图 2.9 中的点 $C$ 是这种类型的间断点,不同之处在于函数 $f\left(x\right)$ 在点 $x=1$ 处无定义.

2. 有限跳跃间断点

在 $x=a$ 时,函数 $f\left(x\right)$ 由一个有限值跳跃到另一个有限值 (如图 2.9 中的点 $A,F,G)$ . 函数 $f\left(x\right)$ 在 $x=a$ 时可能像点 $G$ 那样没有定义; 或 $f\left(a\right)$ 等于 $f\left(a-0\right)$ 与 $f\left(a+0\right)$ 之一 (点 $F$ ); 或 $f\left(a\right)$ 与 $f\left(a-0\right)$ 和 $f\left(a+0\right)$ 均不相等 (点 $A$ ).

$◼\mathbf{A}$: $f\left(x\right)=\frac{1}{1+{\mathrm{e}}^{\frac{1}{x-1}}},f\left(1-0\right)=1,f\left(1+0\right)=0$ (参见第 70 页图 2.8).

$◼\mathbf{B}$: $f\left(x\right)=E\left(x\right)$ (参见第 64 页图 2.1), $f\left(n-0\right)=n-1,f\left(n+0\right)=n(n$ 为整数).

$◼\mathbf{C}$: $f\left(x\right)=\underset{n\to \mathrm{\infty }}{lim}\frac{1}{1+x^{2n}},f\left(1-0\right)=1,f\left(1+0\right)=0,f\left(1\right)=\frac{1}{2}$ .

3. 可去间断点

设 $\underset{x\to a}{lim}f\left(x\right)$ 存在,即 $f\left(a-0\right)=f\left(a+0\right)$ ,但函数在 $x=a$ 处或者没定义,或者 $f\left(a\right)\ne \underset{x\to a}{lim}f\left(x\right)$ (如 75 页图 2.9 中的点 $D$ ). 因为若定义 $f\left(a\right)=\underset{x\to a}{lim}f\left(x\right)$ ,函数在 $x=a$ 处连续,所以 $x=a$ 称为可去间断点,此时只需在曲线上添加一个点或者改变点 $D$ 的位置,就变为连续曲线. 当 $x=a$ 时对于不同的未定式,若利用洛必达法则或其他方法判断其具有有限极限,则 $x=a$ 为可去间断点.

$◼$ 当 $x\to 0$ 时, $f\left(x\right)=\frac{\sqrt{1+x}-1}{x}$ 是 $\frac{0}{0}$ 型未定式,但是 $\underset{x\to 0}{lim}f\left(x\right)=\frac{1}{2}$ ; 函数

$$f\left(x\right)=\{\begin{array}{ll}\frac{\sqrt{1+x}-1}{x},& x\ne 0\\ \frac{1}{2},& x=0\end{array}$$

是连续函数.

2.1.5.4 初等函数的连续性与间断性

初等函数是其定义域内的连续函数, 在定义域内没有间断点. 下列结论成立:

(1)多项式是处处连续函数.

(2) 设 $P\left(x\right)$ 和 $Q\left(x\right)$ 为多项式,则除了在 $Q\left(x\right)=0$ 处外,对所有点 $x$ ,有理函数 $\frac{P\left(x\right)}{Q\left(x\right)}$ 都连续. 若当 $x=a$ 时, $Q\left(a\right)=0,P\left(a\right)\ne 0$ ,则函数在 $a$ 的两侧趋于 $\pm \mathrm{\infty }$ ,这个点称为极点. 若 $P\left(a\right)=0$ ,但 $a$ 是分母比分子更高重的根 (参见第 56 页 1.6.3.1,2.), 则函数也有一个极点, 否则该间断点是可去间断点.

(3) 无理函数 多项式的根对其定义域内的每个 $x$ 都是连续函数. 若被开方式变号,则其在区间端点处可能是有限值. 在被开方式间断的 $x$ 处,有理函数的根也是间断的.

(4) 三角函数 函数 $\sin x,\cos x$ 处处连续; $\tan x,\sec x$ 在点 $x=\frac{\left(2n+1\right)\pi }{2}$ 处有无穷间断点; 函数 $\cot x,\csc x$ 在点 $x=n\pi (n$ 为整数) 处有无穷间断点.

(5) 反三角函数 函数 $\arctan x,\mathrm{arccot}x$ 处处连续. 因为 $-1\le x\le 1$ ,故 $\arcsin x,\arccos x$ 在区间端点中断,且在端点处单侧连续.

(6) 指数函数 ${\mathrm{e}}^x$ 或 $a^x\left(a>0\right)$ 它们是处处连续函数.

(7) 底数是任意正数的对数函数 $\log x$ 对任意正数 $x$ 函数都连续,因为右极限 $\underset{x\to +0}{lim}\log x=-\mathrm{\infty }$ ,所以函数在 $x=0$ 处中断.

(8) 复合初等函数 它们的连续性可由复合过程中每个初等函数在点 $x$ 的连续性来判断 (也可参见本页 2.1.5.5,2. 中复合函数).

• 求函数 $y=\frac{{\mathrm{e}}^{\frac{1}{x-2}}}{x\sin \sqrt[3]{1-x}}$ 的间断点. $x=2$ 是 $\frac{1}{x-2}$ 的无穷间断点,又 ${\left({\mathrm{e}}^{\frac{1}{x-2}}\right)}_{x=2-0}=0,{\left({\mathrm{e}}^{\frac{1}{x-2}}\right)}_{x=2+0}=\mathrm{\infty }$ ,故 $x=2$ 也是 ${\mathrm{e}}^{\frac{1}{x-2}}$ 的无穷间断点. 当 $x=2$ 时, $y$ 的分母是有限值,因此 $x=2$ 是与图 2.9 点 $C$ 相同的无穷间断点.

当 $x=0$ 时, $\sin \sqrt[3]{1-x}=\sin 1$ ,故分母为 $0.\sin \sqrt[3]{1-x}=0$ 的根为 $\sqrt[3]{1-x}=$ $n\pi$ 或 $x=1-n^3{\pi }^3$ ,其中 $n$ 为任意整数. 而当 $x$ 为上述数时,分子不等于 0,因此点 $x=0,x=1,x=1\pm {\pi }^3,x=1\pm 8{\pi }^3,x=1\pm 27{\pi }^3,\cdots$ 也是函数的间断点, 且与 75 页图 2.9 中的点 $E$ 类似.

2.1.5.5 连续函数的性质

1. 连续函数的和、差、积、商仍为连续函数

若 $f\left(x\right),g\left(x\right)$ 是区间 $\left[a,b\right]$ 上的连续函数,则 $f\left(x\right)\pm g\left(x\right),f\left(x\right)g\left(x\right)$ 也是该区间的连续函数,且若在 $\left[a,b\right]$ 上 $g\left(x\right)\ne 0,\frac{f\left(x\right)}{g\left(x\right)}$ 仍为连续函数.

2. 复合函数 $y=f\left(u\left(x\right)\right)$ 的连续性

若 $u\left(x\right)$ 在 $x=a$ 连续, $f\left(u\right)$ 在 $u=u\left(a\right)$ 连续,则复合函数 $y=f\left(u\left(x\right)\right)$ 在

$x=a$ 连续,且

$$\begin{array}{}\text{(2.31)}& \underset{x\to a}{lim}f\left(u\left(x\right)\right)=f\left(\underset{x\to a}{lim}u\left(x\right)\right)=f\left(u\left(a\right)\right).\end{array}$$

这说明连续函数的连续函数仍为连续函数.

注 反之不成立, 不连续函数的复合函数也可能为连续函数.

3. 波尔查诺定理

若函数 $f\left(x\right)$ 在有限闭区间 $\left[a,b\right]$ 上连续, $f\left(a\right)f\left(b\right)<0$ ,则在此区间上至少有 $f\left(x\right)$ 的一个根,即 $\left[a,b\right]$ 至少有一个内点 $c$ 满足:

$$\begin{array}{}\text{(2.32)}& f\left(c\right)=0,a<c<b.\end{array}$$

上述定理的几何意义为: 若连续函数的图像可以从 $x$ 轴的一侧走向另一侧,则曲线与 $x$ 轴至少有一个交点.

4. 介值定理

若函数 $f\left(x\right)$ 在区间 $\left[a,b\right]$ 上连续,且

$$\begin{array}{}\text{(2.33a)}& f\left(a\right)=A,f\left(b\right)=B,A\ne B,\end{array}$$

则对于任意介于 $A,B$ 之间的数 $C$ ,存在 $c\in \left(a,b\right)$ ,使得

$$\begin{array}{}\text{(2.33b)}& f\left(c\right)=C\left(a<c<b,A<C<B\text{ 或 }B<C<A\right).\end{array}$$

换句话说,对于介于 $A,B$ 的每个值,函数 $f\left(x\right)$ 在(a, b)内至少能有一次取得该值, 或者说一个区间的连续像仍为一个区间.

5. 反函数的存在性

若一个一对一函数是某区间上的连续函数, 则它在该区间严格单调.

若函数 $f\left(x\right)$ 在连通区域 I 上连续,且严格单调递增或递减,则该函数也存在一个连续的、严格单调递增或递减的反函数 $\phi \left(x\right)$ (参见第 67 页 2.1.3.8),其定义域是由 $f\left(x\right)$ 的值域所确定的区域 II(图 2.10).

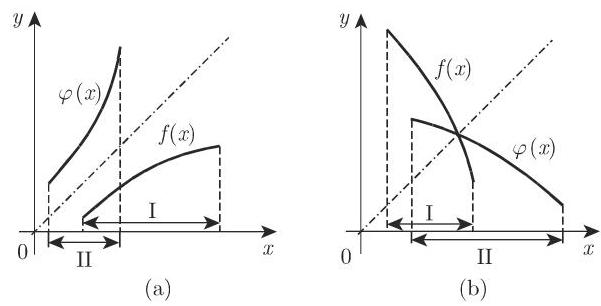
注 为了保障 $f\left(x\right)$ 的反函数的连续性,要求 $f\left(x\right)$ 必须在一个区间连续. 若仅假设函数在区间上严格单调,在内点 $c$ 连续,且 $f\left(c\right)=C$ ,则有反函数存在,但可能在点 $C$ 不连续.

6. 函数有界性定理

若函数 $f\left(x\right)$ 在有限闭区间 $\left[a,b\right]$ 上连续,则它在该区间有界,即存在两个数 $m,M$ ,使得

$$\begin{array}{}\text{(2.34)}& m\le f\left(x\right)\le M,a\le x\le b.\end{array}$$

7. 魏尔斯特拉斯定理

若函数 $f\left(x\right)$ 在有限闭区间 $\left[a,b\right]$ 连续,则 $f\left(x\right)$ 有一个绝对极大值 $M$ 和一个绝对极小值 $m$ ,即该区间至少存在一点 $c$ 和至少存在一点 $d$ ,使得当 $a\le x\le b$ 时, 有

$$\begin{array}{}\text{(2.35)}& m=f\left(d\right)\le f\left(x\right)\le f\left(c\right)=M.\end{array}$$

连续函数最大值与最小值之差称为函数在给定区间的变化量, 变化量的概念可以推广到函数没有最大值和最小值的情形.