Appearance
3.1.6 圆和有关的图形
3.1.6.1 圆
圆是平面上与一个给定点即圆心保持相同给定距离的点的轨迹. 该距离本身, 还有连接圆心与圆上任意点之间的线段称为半径. 圆的圆周环绕着圆的面积. 连接圆上两点的线段称为弦. 穿过圆上两点的直线称为割线. 和圆只有一个公共点的直线称为该圆的切线.
弦定理(图 3.26)
割线定理(图 3.27)
切割线定理(图 3.27)
周长
面积
半径
直径
对于下列与角有关的公式, 见第 168 页 3.1.1.2 中角的定义.
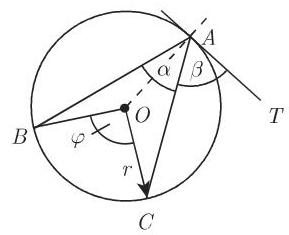
圆周角(图 3.25)
泰勒斯定理的一种特殊情形(参见第 188 页 3.2.1)
弦与切线之间的夹角(图 3.25)
内角(图 3.26)
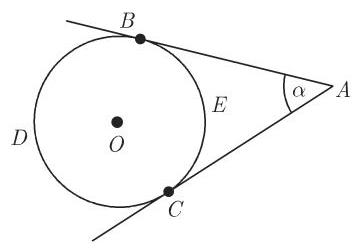
外角(图 3.27)
割线与切线之间的夹角(图 3.27)
切线角 (图 3.28)
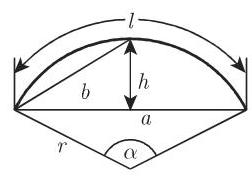
3.1.6.2 圆弓形和圆扇形
定义量 半径
弦
圆心角
弓形的高
弧长
扇形面积
弓形面积
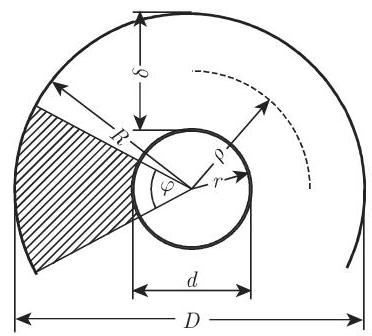
3.1.6.3 圆环
圆环的定义量 外环半径
外环直径
内环直径
平均半径
圆环的宽度
圆环面积
对应圆心角