Appearance
2.13.2 长摆线与短摆线, 或次摆线
当圆沿一直线做无滑动滚动时, 固定在以圆心为始点的半直线上的圆内或圆外一定点经过的轨迹称为长摆线与短摆线, 或次摆线(图 2.68).
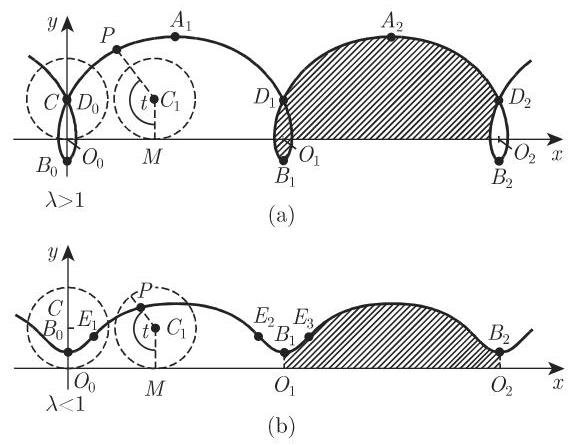
次摆线的参数方程形如
其中
当
曲线为以
极小值点
长摆线有二重点
短摆线有拐点
Appearance
当圆沿一直线做无滑动滚动时, 固定在以圆心为始点的半直线上的圆内或圆外一定点经过的轨迹称为长摆线与短摆线, 或次摆线(图 2.68).

次摆线的参数方程形如
其中
当
曲线为以
极小值点
长摆线有二重点
短摆线有拐点