Appearance
2.12.3 帕斯卡蜗线
(2.232) 中, 原点在圆周上的圆的蚌线称为帕斯卡蜗线(图 2.63), 它是一般蚌线的又一特例 (参见本页 2.12.2). 其笛卡儿坐标形式方程、极坐标方程和参数方程分别为 (也可参见第 136 页 (2.246c))
(2.235c)
其中
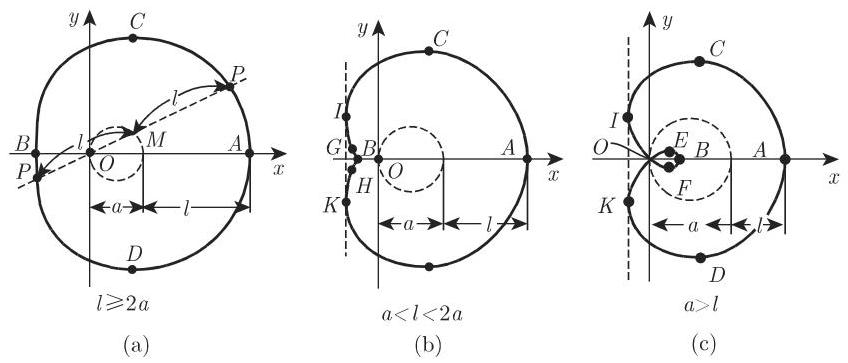
a) 极值点和拐点 若
b) 二重切线 若
c) 奇点 原点为奇点. 若
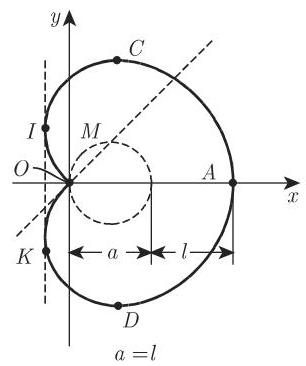
当
蜗线的面积
Appearance
(2.232) 中, 原点在圆周上的圆的蚌线称为帕斯卡蜗线(图 2.63), 它是一般蚌线的又一特例 (参见本页 2.12.2). 其笛卡儿坐标形式方程、极坐标方程和参数方程分别为 (也可参见第 136 页 (2.246c))
(2.235c)
其中

a) 极值点和拐点 若
b) 二重切线 若
c) 奇点 原点为奇点. 若

当
蜗线的面积