Appearance
3.6.2 空间曲线
3.6.2.1 空间曲线的定义方式
1. 坐标方程有下列可能方式用来定义空间曲线:
a) 两曲面的交线
b) 参数形式
其中
c) 参数形式
其中以定点
作为参数.
2. 向量方程
设
而 (3.525a) 可以写成形式
3. 正方向
对于由形式 (3.524) 和 (3.526) 给出的曲线这指的是参数
3.6.2.2 活动三面形
1. 定义
在空间曲线除奇点外的每一点
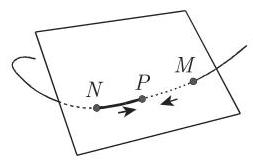
(1) 切线是割线
(2)法平面是与切线垂直的平面 (图 3.239). 在这一平面上通过点
(3) 密切平面是通过三个邻近的点
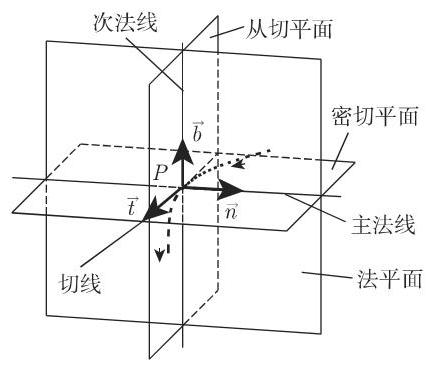
(4) 主法线是法平面与密切平面的交线, 即它是密切平面上的法线.
(5) 次法线是过点
(6) 从切平面是由切线与次法线所展的平面.
(7) 活动三面形, 切线、主法线和次法线上的正方向定义如下:
a) 在切线上由曲线的正方向给出; 单位切向量
b) 在主法线上它由曲线的曲率符号给出,并由单位法向量
c) 在次法线上它由单位向量
确定,其中
2. 相对于活动三面形的曲线位置
对于通常的曲线点,空间曲线在点
(1) 在密切平面上它类似于二次抛物线 (图 3.241(b)).
(2) 在从切平面上它类似于立方抛物线 (图 3.241(c)).
(3) 在法平面上它类似于半立方抛物线 (图 3.241(d)).
如果在
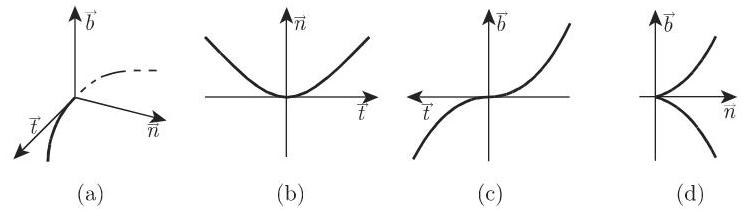
3. 活动三面形构成要素的方程
(1) 按 (3.523) 形式定义的曲线 关于切线见 (3.529), 关于法平面见 (3.530):
这里
(2) 按 (3.524),(3.526) 形式定义的曲线 在表 3.27 中利用
| 向量方程 | 坐标方程 |
|---|---|
| 切线 | |
| 法平面 | |
| 密切平面 | |
| 次法线 | |
| 从切平面 | |
| 主法线 | |
注:
- 关于三向量的混合积, 参见第 249 页, 3.5.1.6, 2.
(3) 按 (3.525a),(3.527) 形式定义的曲线 如果参数是弧长
三面形的要素 | 向量方程 | 坐标方程 |
主法线 | ||
从切平面 |
注:
3.6.2.3 曲率和挠率
1. 曲线的曲率和曲率半径
曲线在点
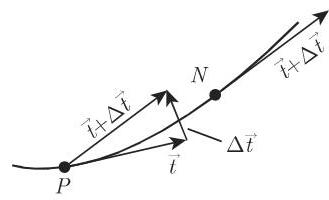
(1)曲率半径 曲率半径是曲率绝对值的倒数:
(2)计算
a) 如果曲线的定义形式为(3.525a),则
其中导数是关于
b) 如果曲线的定义形式为 (3.524), 则
这里导数是关于
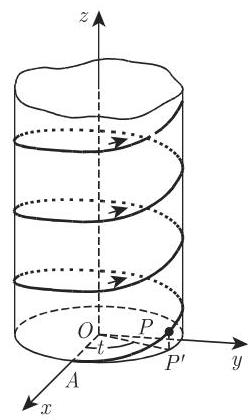
(3) 螺旋线 方程
刻画的是一条右手螺旋线 (图 3.243). 如果观察者注视
根据 (3.533),
另一种方法, 不用在 (3.534) 中作参数变换, 也产生同样的结果.
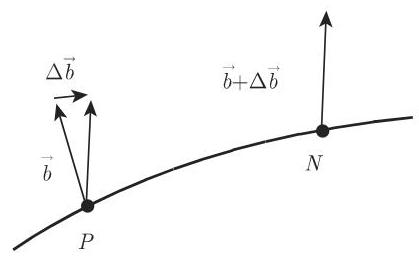
2. 曲线的挠率和挠率圆的半径
曲线在点
挠率半径是
- 计算
和 的公式
a) 如果曲线的定义形式为(3.525a),则
其中导数是关于
b) 如果曲线的定义形式为 (3.524), 则
其中
用 (3.538),(3.539) 计算的挠率可以是正的也可以是负的. 在
- 螺旋线的挠率是常数. 用记号
表示右旋, 表示左旋,则挠率为
- 关于三个向量的混合积, 参见第 249 页 3.5.1.6, 2.
3. 弗雷内 (Frenet) 公式
向量
其中
4. 达布 (Darboux) 向量
弗雷内公式 (3.540) 也可以用更容易记忆的形式 (达布公式) 表示
其中
评论 (1) 借助达布向量可以在运动学的意义上解释弗雷内公式 (见 [3.18]).
(2)达布向量的模等于空间曲线的全曲率