Appearance
12.2.1 距离空间
设
(M1)
(M2)
(M3)
在距离空间
也是
对于
也定义
IF: 在集合
12.2.1.1 球, 邻域和开集
距离空间
分别称作以
在向量空间
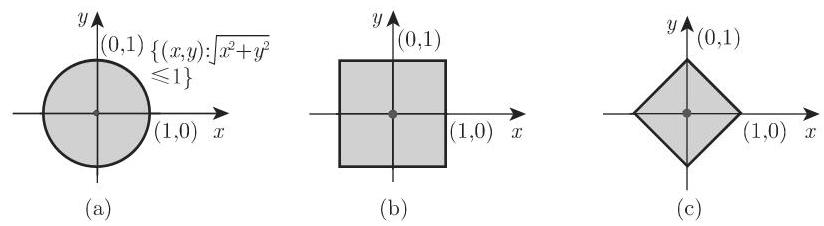
距离空间
每个距离空间中的开球,特别是
所有开集的集合满足如下的开集公理:
如果
是开集, ,则集合 也是开集. 如果
是任意有穷个开集,则集合 也是开集. 空集
按定义是开集.
距离空间中的一个子集
12.2.1.2 距离空间中的序列收敛
设
而点
利用特定距离空间中引入的这些概念, 就可以计算点与点之间的距离, 并研究点列的收敛性. 在数值方法以及利用某些函数类的函数逼近中, 这是非常重要的 (例如, 参见第 1276 页 19.6).
如果在空间
在空间
在空间
12.2.1.3 闭集和闭包
1. 闭集
距离空间
根据开集的公理, 距离空间中所有闭集组成的集族具有如下性质:
如果
是闭的, ,则 是闭的. 如果
是有穷多个闭集,则集合 是闭的. 空集
依据定义是闭集.
集合
距离空间
如果对于任意邻域
如果存在
2. 集合的闭包
距离空间
12.2.1.4 稠子集和可分距离空间
距离空间
距离空间