19.7.3 曲线和曲面的伯恩斯坦-贝济埃表示

1. 伯恩斯坦-贝济埃多项式

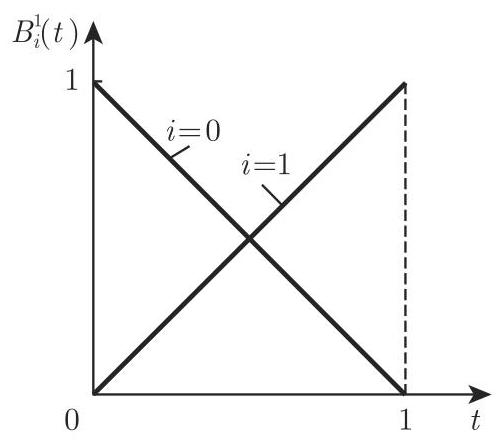
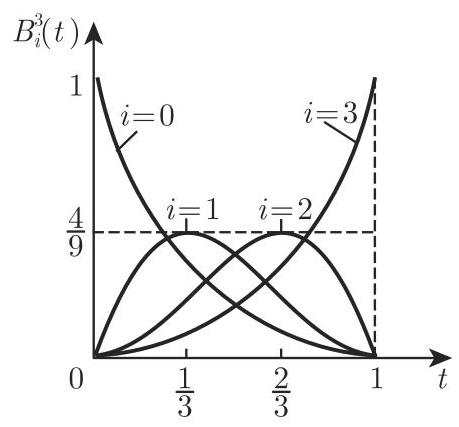
曲线和曲面的伯恩斯坦-贝济埃 (Bernstein-Bézier) 表示 (简记 B-B 表示) 使用伯恩斯坦多项式

$$\begin{array}{}\text{(19.252)}& B_{i,n}\left(t\right)=\left(\begin{array}{c}n\\ i\end{array}\right)t^i{(1-t)}^{n-i}\left(i=0,1,\cdots ,n\right)\end{array}$$

并利用如下基本性质:

(1)

$$\begin{array}{}\text{(19.253)}& 0\le B_{i,n}\left(t\right)\le 1,0\le t\le 1,\end{array}$$

(2)

$$\begin{array}{}\text{(19.254)}& \sum _{i=0}^n{B}_{i,n}\left(t\right)=1\end{array}$$

公式 (19.254) 由二项式定理 (参见第 14 页 1.1.6.4) 直接得到.

$\mathbf{A}:B_{01}\left(t\right)=1-t,B_{1,1}\left(t\right)=t$ (图 19.12).

$\mathbf{B}:B_{03}\left(t\right)={(1-t)}^3,B_{1,3}\left(t\right)=3t{(1-t)}^2,B_{2,3}\left(t\right)=3t^2\left(1-t\right)B_{3,3}\left(t\right)=t^3$(图 19.13).

2. 向量表示

参数表达式为 $x=x\left(t\right),y=y\left(t\right),z=z\left(t\right)$ 的空间曲线记为向量形式

$$\begin{array}{}\text{(19.255)}& \overrightarrow{r}=\overrightarrow{r}\left(t\right)=x\left(t\right){\overrightarrow{e}}_x+y\left(t\right){\overrightarrow{e}}_y+z\left(t\right){\overrightarrow{e}}_z,\end{array}$$

这里 $t$ 为曲线的参数. 相应的曲面表达式为

$$\begin{array}{}\text{(19.256)}& \overrightarrow{r}=\overrightarrow{r}\left(u,v\right)=x\left(u,v\right){\overrightarrow{e}}_x+y\left(u,v\right){\overrightarrow{e}}_y+z\left(u,v\right){\overrightarrow{e}}_z.\end{array}$$

其中 $u$ 和 $v$ 为曲面参数.

19.7.3.1 B-B 曲线表示的原理

设给定位置向量为 ${\overrightarrow{P}}_i$ 的三维多边形的 $n+1$ 个顶点 $P_i\left(i=0,1,\cdots ,n\right)$ . 引入向量值函数

$$\begin{array}{}\text{(19.257)}& \overrightarrow{r}\left(t\right)=\sum _{i=0}^n{B}_{i,n}\left(t\right){\overrightarrow{P}}_i.\end{array}$$

由这些点确定的空间曲线称为 B-B 曲线. 由于 (19.254)、公式 (19.257) 可看作这些给定点的 “变量凸组合”. 三维曲线 (19.257) 有如下重要性质:

(1) $P_0$ 和 $P_n$ 为插值点.

(2) 向量 $\overrightarrow{P_0{P}_1}$ 和向量 $\overrightarrow{P_{n-1}{P}_n}$ 为点 $P_0$ 和 $P_n$ 处 $\overrightarrow{r}\left(t\right)$ 的切线.

多边形与 B-B 曲线间的关系见图 19.14.

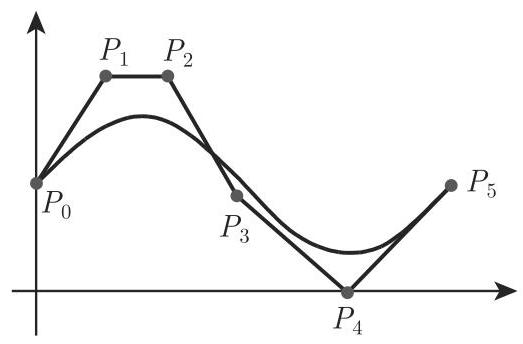
B-B 表示可用来设计曲线, 因为通过改变多边形的顶点容易改变曲线的形状.

常用正则化的 $\mathrm{B}$ 样条代替伯恩斯坦多项式.

相应的空间曲线称为 $\mathrm{B}$ 样条曲线. 其形状基本相应于有如下优点的 $\mathrm{B}-\mathrm{B}$ 曲线:

(1)更好逼近多边形.

(2) 若改变多边形顶点, 仅局部改变 $\mathrm{B}$ 样条曲线.

(3) 除局部改变曲线形状外, 也可能影响其可微性.

因此, 可能产生间断的点和线段.

19.7.3.2 B-B 曲面表示

设给定位置向量为 ${\overrightarrow{P}}_{ij}$ 的点 $P_{ij}\left(i=0,1,\cdots ,n;j=0,1,\cdots ,m\right)$ ,可以考虑沿曲面参数曲线的网格节点. 类似于 B-B 曲线 (19.257), 对网格节点由

$$\begin{array}{}\text{(19.258)}& \overrightarrow{r}\left(u,v\right)=\sum _{i=0}^n\sum _{j=0}^m{B}_{i,n}\left(u\right)B_{j,m}\left(v\right){\overrightarrow{P}}_{ij}\end{array}$$

确定曲面. 因为改变网格节点就能改变曲面, 表达式 (19.258) 对于曲面设计是有用的. 但是, 每个格点的影响是全局的, 故应该将伯恩斯坦多项式改为 (19.258) 中的 B 样条.