8.2.3 广义积分、斯蒂尔切斯积分与勒贝格积分

8.2.3.1 积分概念的推广

前面已经把定积分作为黎曼积分 (参见第 657 页 8.2.1.1) 介绍了它的概念, 当时假设函数 $f\left(x\right)$ 有界, $\left[a,b\right]$ 为有限闭区间. 在黎曼积分的推广中这两个条件都可以放宽, 接来下将会提到.

1. 广义积分

广义积分把被积函数推广到无界函数或者无限区间. 下面几段会讨论无限积分区间的积分和无界被积函数的积分.

2. 一元函数的斯蒂尔切斯积分

设在有限区间 $\left[a,b\right]$ 上给定两个有限函数 $f\left(x\right)$ 和 $g\left(x\right)$ . 正如黎曼积分一样, 把区间 $\left[a,b\right]$ 划分成一系列子区间,但与黎曼和 (8.38) 不同,此处考虑如下形式的和:

$$\begin{array}{}\text{(8.76)}& \sum _{i=1}^{n}f\left({\xi }_i\right)\left[g\left(x_i\right)-g\left(x_{i-1}\right)\right].\end{array}$$

若无论如何选取点 $x_i$ 和 ${\xi }_i$ ,都有当子区间的长度趋于 0 时,极限 (8.76) 存在,则称该极限为定斯蒂尔切斯 (Stieltjes) 积分 (也可参见 [8.14], [8.19]).

若 $g\left(x\right)=x$ ,则斯蒂尔切斯积分变成黎曼积分.

3. 勒贝格积分

积分的另一种推广与测度论有关 (参见第 905 页 12.9), 涉及集合的测度、测度空间、可测函数的概念. 泛函分析中的勒贝格积分正是以这些概念为基础 (参见 [8.10]) 定义的 (参见第 908 页 12.9.3.2). 相比黎曼积分而言, 这种推广可以把积分区域推广到 ${\mathbb{R}}^n$ 的更一般的子集上,把积分区域划分成可测子集.

关于积分的推广还有不同的记号 (参见 [8.14]).

8.2.3.2 具有无限积分限的积分

1. 定义

a) 若被积函数的积分区间为闭半轴 $[a,+\mathrm{\infty })$ ,则该积分可定义为

$$\begin{array}{}\text{(8.77)}& {\int }_a^{+\mathrm{\infty }}f\left(x\right)\mathrm{d}x=\underset{B\to \mathrm{\infty }}{lim}{\int }_a^{B}f\left(x\right)\mathrm{d}x.\end{array}$$

若极限存在, 则称该积分为收敛广义积分; 若极限不存在, 则广义积分 (8.77) 发散.

b) 若函数的定义域为闭半轴 $(-\mathrm{\infty },b]$ 或整个实数轴 $\left(-\mathrm{\infty },+\mathrm{\infty }\right)$ ,则可类似地把广义积分定义成

$$\begin{array}{}\text{(8.78a)}& {\int }_{-\mathrm{\infty }}^{b}f\left(x\right)\mathrm{d}x=\underset{A\to -\mathrm{\infty }}{lim}{\int }_A^{b}f\left(x\right)\mathrm{d}x,\end{array}$$$$\begin{array}{}\text{(8.78b)}& {\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}f\left(x\right)\mathrm{d}x=\underset{\begin{array}{c}A\to -\mathrm{\infty }\\ B\to \mathrm{\infty }\end{array}}{lim}{\int }_A^{B}f\left(x\right)\mathrm{d}x.\end{array}$$

c) (8.78b) 的上下限 $A,B$ 都趋于无穷且相互独立,若极限 (8.78b) 不存在,但极限

$$\begin{array}{}\text{(8.78c)}& \underset{A\to \mathrm{\infty }}{lim}{\int }_{-A}^{+A}f\left(x\right)\mathrm{d}x\end{array}$$

存在, 则极限 (8.78c) 称为广义积分主值或柯西主值.

注 显然, $\underset{x\to \mathrm{\infty }}{lim}f\left(x\right)=0$ 是积分 (8.77) 收敛的必要非充分条件.

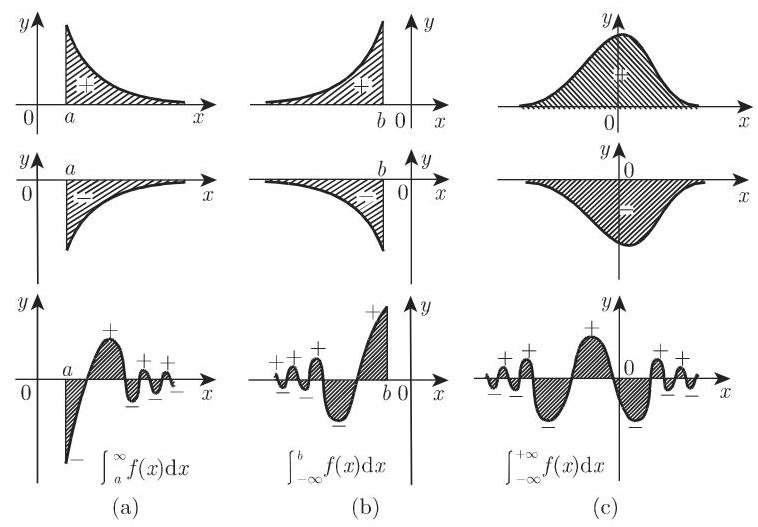
2. 无穷积分限积分的几何意义

积分 (8.77), (8.78a), (8.78b) 分别表示图 8.21 所示图形的面积.

$◼\mathbf{A}$: ${\int }_1^{\mathrm{\infty }}\frac{\mathrm{d}x}{x}=\underset{B\to \mathrm{\infty }}{lim}{\int }_1^B\frac{\mathrm{d}x}{x}=\underset{B\to \mathrm{\infty }}{lim}\ln \left|B\right|=\mathrm{\infty }$ (发散).

$◼\mathbf{B}$: ${\int }_2^{\mathrm{\infty }}\frac{\mathrm{d}x}{x^2}=\underset{B\to \mathrm{\infty }}{lim}{\int }_2^B\frac{\mathrm{d}x}{x^2}=\underset{B\to \mathrm{\infty }}{lim}\left(\frac{1}{2}-\frac{1}{B}\right)=\frac{1}{2}$ (收敛).

$◼\mathbf{C}$: ${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\mathrm{d}x}{1+x^2}=\underset{\begin{array}{c}A\to -\mathrm{\infty }\\ B\to \mathrm{\infty }\end{array}}{lim}{\int }_A^B\frac{\mathrm{d}x}{1+x^2}=\underset{\begin{array}{c}A\to -\mathrm{\infty }\\ B\to \mathrm{\infty }\end{array}}{lim}\left[\arctan B-\arctan A\right]=\frac{\pi }{2}-$

$$\left(-\frac{\pi }{2}\right)=\pi \text{(收敛).}$$

3. 收敛的充分条件

若直接计算极限 (8.77), (8.78a) 和 (8.78b) 比较复杂, 或者只需判断一个广义积分的敛散性, 则可利用下面的充分条件之一. 此处仅考虑 (8.77), 因为 (8.78a) 可以用 $-x$ 代换 $x$ ,进一步转换成 (8.77) 的形式:

$$\begin{array}{}\text{(8.79)}& {\int }_{-\mathrm{\infty }}^{a}f\left(x\right)\mathrm{d}x={\int }_{-a}^{+\mathrm{\infty }}f\left(-x\right)\mathrm{d}x.\end{array}$$

而积分 (8.78b) 可分解成形如 (8.77) 和 (8.78a) 的两个积分之和:

$$\begin{array}{}\text{(8.80)}& {\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}f\left(x\right)\mathrm{d}x={\int }_{-\mathrm{\infty }}^{c}f\left(x\right)\mathrm{d}x+{\int }_c^{+\mathrm{\infty }}f\left(x\right)\mathrm{d}x,\end{array}$$

其中 $c$ 为任意实数.

充分条件 1 若 $f$ 在任意无限 ${}^{\text{①}}$ 区间 $[a,+\mathrm{\infty })$ 上都可积,且积分

$$\begin{array}{}\text{(8.81)}& {\int }_a^{+\mathrm{\infty }}\left|f\left(x\right)\right|\mathrm{d}x\end{array}$$

收敛,则积分 (8.77) 也收敛. 此时称 (8.77) 为绝对收敛,称函数 $f\left(x\right)$ 在半轴 $[a,+\mathrm{\infty })$ 上绝对可积.

充分条件 2 若函数 $f\left(x\right)$ 和 $\phi \left(x\right)$ 满足

$$\begin{array}{}\text{(8.82a)}& f\left(x\right)>0,\phi \left(x\right)>0\text{ 且当 }a\le x<+\mathrm{\infty }\text{ 时 }f\left(x\right)\le \phi \left(x\right),\end{array}$$

则由积分

$$\begin{array}{}\text{(8.82b)}& {\int }_a^{+\mathrm{\infty }}\phi \left(x\right)\mathrm{d}x\end{array}$$

---

① 原文有误. ——译者注

---

收敛可得积分

$$\begin{array}{}\text{(8.82c)}& {\int }_a^{+\mathrm{\infty }}f\left(x\right)\mathrm{d}x\end{array}$$

收敛; 反之可由 (8.82c) 发散得 (8.82b) 发散.

充分条件 3 设有代换

$$\begin{array}{}\text{(8.83a)}& \phi \left(x\right)=\frac{1}{x^{\alpha }},\end{array}$$

当 $a>0,\alpha >1$ 时积分

$$\begin{array}{}\text{(8.83b)}& {\int }_a^{+\mathrm{\infty }}\frac{\mathrm{d}x}{x^{\alpha }}=\frac{1}{\left(\alpha -1\right)a^{\alpha -1}}\left(a>0,\alpha >1\right)\end{array}$$

收敛且等于右侧的值,当 $\alpha \le 1$ 时左侧积分发散,可得到进一步的收敛条件:

若当 $a\le x<\mathrm{\infty }$ 时函数 $f\left(x\right)$ 为正,且至少存在一个数 $\alpha >1$ ,使得对任意足够大的 $x$ ,都有

$$\begin{array}{}\text{(8.83c)}& f\left(x\right)x^{\alpha }<k<\mathrm{\infty }\left(k>0\text{ 且为常数 }\right),\end{array}$$

则积分 (8.77) 收敛; 若 $f\left(x\right)$ 为正,且存在一个数 $\alpha \le 1$ ,使得自某个 $x$ 之后,都有

$$\begin{array}{}\text{(8.83d)}& f\left(x\right)x^{\alpha }>c>0\left(c>0\text{ 且为常数 }\right),\end{array}$$

则积分 (8.77) 发散.

$◼{\int }_0^{+\mathrm{\infty }}\frac{x^{3/2}\mathrm{d}x}{1+x^2}$ . 取 $\alpha =\frac{1}{2}$ ,有 $\frac{x^{3/2}}{1+x^2}{x}^{1/2}=\frac{x^2}{1+x^2}\to 1$ ,故积分发散.

4. 广义积分与无穷级数的关系

若 $x_1,x_2,\cdots ,x_n,\cdots$ 为任意无限增加的无穷序列,即若

$$\begin{array}{}\text{(8.84a)}& a<x_1<x_2<\cdots <x_n<\cdots ,\underset{n\to +\mathrm{\infty }}{lim}{x}_n=\mathrm{\infty },\end{array}$$

且当 $a\le x<\mathrm{\infty }$ 时函数 $f\left(x\right)$ 为正,则积分 (8.77) 的收敛问题可化成级数

$$\begin{array}{}\text{(8.84b)}& {\int }_a^{x_1}f\left(x\right)\mathrm{d}x+{\int }_{x_1}^{x_2}f\left(x\right)\mathrm{d}x+\cdots +{\int }_{x_{n-1}}^{x_n}f\left(x\right)\mathrm{d}x+\cdots \end{array}$$

的收敛问题. 若级数 (8.84b) 收敛, 则积分 (8.77) 也收敛且等于 (8.84b) 的和. 若级数 (8.84b) 发散, 则积分 (8.77) 也发散. 因此可以把级数的收敛条件用于广义积分, 反之, 由级数的积分审敛法 (参见第 619 页 7.2.2.4), 可用广义积分来研究无穷级数的收敛性.

8.2.3.3 无界被积函数的积分

1. 定义

(1)右开区间 设函数 $f\left(x\right)$ 的定义域为右开区间 $[a,b)$ ,且在点 $b$ 其非正常极限 $\underset{x\to b-0}{lim}f\left(x\right)=\mathrm{\infty }$ ,则可如下定义广义积分:

$$\begin{array}{}\text{(8.85)}& {\int }_a^{b}f\left(x\right)\mathrm{d}x=\underset{\epsilon \to +0}{lim}{\int }_a^{b-\epsilon }f\left(x\right)\mathrm{d}x.\end{array}$$

若该极限存在且有限, 则广义积分 (8.85) 存在, 称其为收敛广义积分; 若该极限不存在或为无限, 则称其为发散广义积分.

(2) 左开区间 设函数 $f\left(x\right)$ 的定义域为左开区间 $(a,b]$ ,且在点 $a$ 有 $\underset{x\to a+0}{lim}f\left(x\right)$ $=\mathrm{\infty }$ ,则与 (8.85) 类似可如下定义广义积分:

$$\begin{array}{}\text{(8.86)}& {\int }_a^{b}f\left(x\right)\mathrm{d}x=\underset{\epsilon \to +0}{lim}{\int }_{a+\epsilon }^{b}f\left(x\right)\mathrm{d}x.\end{array}$$

(3) 双半开连续区间 若函数 $f\left(x\right)$ 除了在区间 $\left[a,b\right]$ 的内点 $c\left(a<c<b\right)$ 外都有定义,也就是函数定义在区间 $\left[a,c)\text{和}(c,b\right]$ 上,或者定义在 $\left[a,b\right]$ 上,但在内点 $c$ 处至少有一侧极限为无穷,即 $\underset{x\to c+0}{lim}f\left(x\right)=\mathrm{\infty }$ 或 $\underset{x\to c-0}{lim}f\left(x\right)=\mathrm{\infty }$ ,则广义积分可定义为

$$\begin{array}{}\text{(8.87a)}& {\int }_a^{b}f\left(x\right)\mathrm{d}x=\underset{\epsilon \to +0}{lim}{\int }_a^{c-\epsilon }f\left(x\right)\mathrm{d}x+\underset{\delta \to +0}{lim}{\int }_{c+\delta }^{b}f\left(x\right)\mathrm{d}x.\end{array}$$

其中 $\epsilon$ 和 $\delta$ 彼此独立地趋近于 0. 若极限 (8.87a) 不存在,但是极限

$$\begin{array}{}\text{(8.87b)}& \underset{\epsilon \to +0}{lim}\left\{{\int }_a^{c-\epsilon }f\left(x\right)\mathrm{d}x+{\int }_{c+\epsilon }^{b}f\left(x\right)\mathrm{d}x\right\}\end{array}$$

存在, 则 (8.87b) 称为广义积分主值或柯西主值.

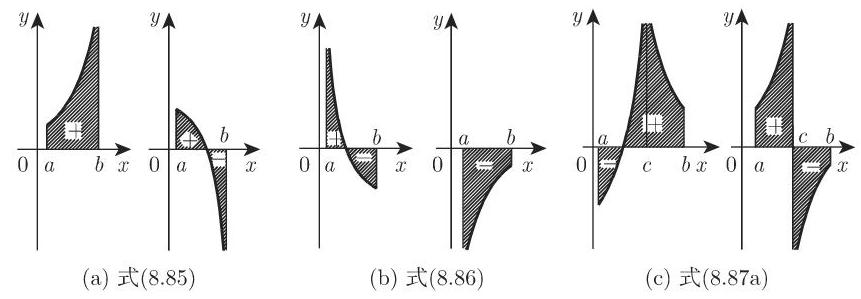
2. 几何意义

无界函数 (8.85), (8.86) 和 (8.87a) 的几何意义是求如图 8.22 所示的以一侧垂直渐近线为边界的图形的面积.

$◼\mathbf{A}$: ${\int }_0^b\frac{\mathrm{d}x}{\sqrt{x}}$ 满足 (8.86) 的情形, $x=0$ 为奇点.

$${\int }_0^b\frac{\mathrm{d}x}{\sqrt{x}}=\underset{\epsilon \to +0}{lim}{\int }_{\epsilon }^b\frac{\mathrm{d}x}{\sqrt{x}}=\underset{\epsilon \to +0}{lim}\left(2\sqrt{b}-2\sqrt{\epsilon }\right)=2\sqrt{b}\text{ (收敛). }$$

$◼\mathbf{B}$: ${\int }_0^{\pi /2}\tan x\mathrm{d}x$ 满足 (8.85) 的情形, $x=\frac{\pi }{2}$ 为奇点.

$${\int }_0^{\pi /2}\tan x\mathrm{d}x=\underset{\epsilon \to +0}{lim}{\int }_0^{\pi /2-\epsilon }\tan x\mathrm{d}x$$$$=\underset{\epsilon \to +0}{lim}\left[\ln \cos 0-\ln \cos \left(\frac{\pi }{2}-\epsilon \right)\right]=\mathrm{\infty }\text{ (发散). }$$

$◼\mathbf{C}$: ${\int }_{-1}^8\frac{\mathrm{d}x}{\sqrt[3]{x}}$ 满足(8.87a)的情形, $x=0$ 为奇点.

$${\int }_{-1}^8\frac{\mathrm{d}x}{\sqrt[3]{x}}=\underset{\epsilon \to +0}{lim}{\int }_{-1}^{-\epsilon }\frac{\mathrm{d}x}{\sqrt[3]{x}}+\underset{\delta \to +0}{lim}{\int }_{\delta }^8\frac{\mathrm{d}x}{\sqrt[3]{x}}$$$$=\underset{\epsilon \to +0}{lim}\frac{3}{2}\left({\epsilon }^{2/3}-1\right)+\underset{\delta \to +0}{lim}\frac{3}{2}\left(4-{\delta }^{2/3}\right)=\frac{9}{2}\text{ (收敛). }$$

$◼\mathbf{D}$: ${\int }_{-2}^2\frac{2x\mathrm{d}x}{x^2-1}$ 满足(8.87a)的情形, $x=\pm 1$ 为奇点.

$${\int }_{-2}^2\frac{2x\mathrm{d}x}{x^2-1}=\underset{\epsilon \to +0}{lim}{\int }_{-2}^{-1-\epsilon }+\underset{\begin{array}{c}\delta \to +0\\ \nu \to +0\end{array}}{lim}{\int }_{-1+\delta }^{1-\nu }+\underset{\gamma \to +0}{lim}{\int }_{1+\gamma }^2={\underset{\epsilon \to +0}{lim}\ln |x^2-1||}_{-2}^{-1-\epsilon }+\cdots$$$$=\underset{\epsilon \to +0}{lim}\left[\ln \left|1+2\epsilon +{\epsilon }^2-1\right|-\ln 3\right]+\cdots =\mathrm{\infty }\text{ (发散). }$$

3. 微积分基本定理的应用

(1) 注意 在计算形如 (8.87a) 的广义积分时,若不考虑区间 $\left[a,b\right]$ 中的奇点, 直接利用公式

$$\begin{array}{}\text{(8.88)}& {\int }_a^{b}f\left(x\right)\mathrm{d}x={F\left(x\right)|}_a^b,\text{ 其中 }{F}^{\prime }\left(x\right)=f\left(x\right)\end{array}$$

(参见第 667 页 8.2.2.2, 1.), 则会得到错误的结论.

$◼\mathbf{E}$: 例如在例 D 中尽管 ${\int }_{-2}^2\frac{2x\mathrm{d}x}{x^2-1}$ 发散,但若形式地使用基本定理,则有

$${\int }_{-2}^2\frac{2x\mathrm{d}x}{x^2-1}={\ln |x^2-1||}_{-2}^2=\ln 3-\ln 3=0.$$

(2)一般法则 仅当 $f\left(x\right)$ 的原函数在奇点连续时,(8.87a) 才可以使用微积分基本定理.

$◼\mathbf{F}$: 例如在例 $\mathrm{D}$ 中,函数 $\ln \left|x^2-1\right|$ 在 $x=\pm 1$ 处不连续,因此条件不成立. 而在例 $\mathrm{C}$ 中,函数 $y=\frac{3}{2}{x}^{2/3}$ 是区间 $\left[a,0)\text{和}(0,b\right]$ 上 $\frac{1}{\sqrt[3]{x}}$ 的一个原函数,且在 $x=0$ 处连续, 因此可利用微积分基本定理:

$${\int }_{-1}^8\frac{\mathrm{d}x}{\sqrt[3]{x}}={\frac{3}{2}{x}^{2/3}|}_{-1}^8=\frac{3}{2}\left(8^{2/3}-{(-1)}^{2/3}\right)=\frac{9}{2}.$$

4. 无界被积函数 $\underset{x\to b-0}{lim}f\left(x\right)=\mathrm{\infty }$ 广义积分收敛的充分条件

(1)若广义积分 ${\int }_a^b\left|f\left(x\right)\right|\mathrm{d}x$ 收敛,则广义积分 ${\int }_a^{b}f\left(x\right)\mathrm{d}x$ 也收敛,此时称之为绝对收敛积分,称定义区间上的函数 $f\left(x\right)$ 为绝对可积函数.

(2) 若在区间 $[a,b)$ 上函数 $f\left(x\right)$ 为正,且存在数 $\alpha <1$ ,使得对与 $b$ 足够接近的所有 $x$ ,都有

$$\begin{array}{}\text{(8.89a)}& f\left(x\right){(b-x)}^{\alpha }<\mathrm{\infty },\end{array}$$

则积分 (8.87a) 收敛. 但是若在区间 $[a,b)$ 上函数 $f\left(x\right)$ 为正,且存在数 $\alpha >1$ ,使得对与 $b$ 足够接近的 $x$ ,有

$$\begin{array}{}\text{(8.89b)}& f\left(x\right){(b-x)}^{\alpha }>c>0\left(c\text{ 为常数 }\right),\end{array}$$

则积分 (8.87a) 发散.