2.18.3 极限

2.18.3.1 定义

若当 $x,y$ 分别以任意方式趋近于 $a,b$ 时,二元函数 $u=f\left(x,y\right)$ 的值任意趋近于值 $A$ ,则称函数 $u=f\left(x,y\right)$ 在 $x=a,y=b$ 处的极限为 $A$ ,记为

$$\begin{array}{}\text{(2.284)}& \underset{\begin{array}{c}x\to a\\ y\to b\end{array}}{lim}f\left(x,y\right)=A\end{array}$$

函数可能在点(a, b)没定义,或有定义但 $f\left(a,b\right)\ne A$ .

2.18.3.2 精确定义

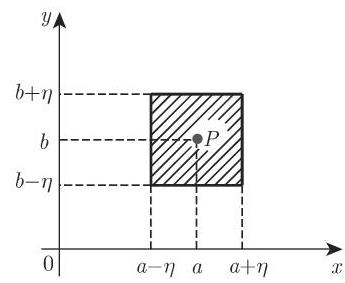
若对任意给定的正数 $\epsilon$ ,总存在正数 $\eta$ ,使得对于正方形

$$\begin{array}{}\text{(2.285a)}& \left|x-a\right|<\eta ,\left|y-b\right|<\eta \end{array}$$

内的每个点(x, y)(参见图 2.107),都有

$$\begin{array}{}\text{(2.285b)}& \left|f\left(x,y\right)-A\right|<\epsilon ,\end{array}$$

则称二元函数 $u=f\left(x,y\right)$ 在点(a, b)处有极限

$$\begin{array}{}\text{(2.285c)}& A=\underset{\begin{array}{c}x\to a\\ y\to b\end{array}}{lim}f\left(x,y\right).\end{array}$$

2.18.3.3 向多元函数的推广

a) 与二元函数类似, 可以定义多元函数极限的概念.

b) 把一元函数极限的判别方法进行推广, 可得多元函数极限的判别方法, 即化简成一个序列的极限或者利用柯西收敛条件 (参见第 69 页 2.1.4.3).

2.18.3.4 累次极限

若首先确定出二元函数 $f\left(x,y\right)$ 在 $x\to a,y$ 为常数时的极限,再把它看成 $y$ 的函数,求 $y\to b$ 时的极限,则最终结果

$$\begin{array}{}\text{(2.286a)}& B=\underset{y\to b}{lim}\left(\underset{x\to a}{lim}f\left(x,y\right)\right)\end{array}$$

称为累次极限. 改变计算顺序通常会得到另一个极限

$$\begin{array}{}\text{(2.286b)}& C=\underset{x\to a}{lim}\left(\underset{y\to b}{lim}f\left(x,y\right)\right).\end{array}$$

一般地,即使两个极限都存在,也有 $B\ne C$ .

$◼$ 当 $x\to 0,y\to 0$ 时,函数 $f\left(x,y\right)=\frac{x^2-y^2+x^3+y^3}{x^2+y^2}$ 的累次极限 $B=-1,C=$ $+1$ .

注 若函数 $f\left(x,y\right)$ 的极限 $A=\underset{\begin{array}{c}x\to a\\ y\to b\end{array}}{lim}f\left(x,y\right)$ ,且 $B,C$ 均存在,则 $B=C=A$ . 由极限 $A$ 的存在性不能得到极限 $B,C$ 的存在性,同样由极限 $B=C$ 也不能得到极限 $A$ 的存在性.