6.1.2 一元函数微分法则

6.1.2.1 初等函数的导数

如图 6.2 所示, 除某些点外, 初等函数在整个定义域内均可导.

初等函数导数公式见表 6.1 , 此外初等函数的导数也可利用表 8.1 中不定积分的逆运算来得到.

函数	导数	函数	导数
$C$ (常数)	0	$\sec x$	$\frac{\sin x}{{\cos }^{2}x}$
$x$	1	cosecx	$\frac{-\cos x}{{\sin }^{2}x}$
$x^n\left(n\in \mathbb{R}\right)$	$n{x}^{n-1}$	$\arcsin x\left(\left|x\right|<1\right)$	$\frac{1}{\sqrt{1-x^2}}$
$\frac{1}{x}\left(x\ne 0\right)$	$-\frac{1}{x^2}\left(x\ne 0\right)$	$\arccos x\left(\left|x\right|<1\right)$	$-\frac{1}{\sqrt{1-x^2}}$
$\frac{1}{x^n}\left(x\ne 0\right)$	$-\frac{n}{x^{n+1}}$	$\arctan x$	$\frac{1}{1+x^2}$
$\sqrt{x}\left(x>0\right)$	$\frac{1}{2\sqrt{x}}$	arccot $x$	$-\frac{1}{1+x^2}$
$\sqrt[n]{x}\left(n\in \mathbb{R},n\ne 0,x>0\right)$	$\frac{1}{n\sqrt[n]{x^{n-1}}}$	$\mathrm{arcsec}x\left(x>1\right)$	$\frac{1}{x\sqrt{x^2-1}}$
${\mathrm{e}}^x$	${\mathrm{e}}^x$	$\mathrm{arccosec}\left(x>1\right)$	$-\frac{1}{x\sqrt{x^2-1}}$
${\mathrm{e}}^{bx}\left(b\in \mathbb{R}\right)$	$b{\mathrm{e}}^{bx}$	$\sinh x$	$\cosh x$
$a^x\left(a>0\right)$	$a^x\ln a$	$\cosh x$	$\sinh x$
$a^{bx}\left(b\in \mathbb{R},a>0\right)$	$b{a}^{bx}\ln a$	$\tanh x$	$\frac{1}{{\cosh }^{2}x}$
$\ln x\left(x>0\right)$	$\frac{1}{x}$	$\coth x\left(x\ne 0\right)$	$-\frac{1}{{\sinh }^{2}x}$
${\log }_{a}x\left(a>0,a\ne 1,x>0\right)$	$\frac{1}{x}{\log }_a\mathrm{e}=\frac{1}{x\ln a}$	Arsinhx	$\frac{1}{\sqrt{1+x^2}}$
$\lg x\left(x>0\right)$	$\frac{1}{x}\lg \mathrm{e}\approx \frac{0.4343}{x}$	$\mathrm{Arcosh}x\left(x>1\right)$	$\frac{1}{\sqrt{x^2-1}}$
$\sin x$	$\cos x$	Artanh $x\left(\left|x\right|<1\right)$	$\frac{1}{1-x^2}$
$\cos x$	$-\sin x$	Arcoth $x\left(\left|x\right|>1\right)$	$-\frac{1}{x^2-1}$
$\tan x\left(x\ne \left(2k+1\right)\frac{\pi }{2},k\in \mathbb{Z}\right)$	$\frac{1}{{\cos }^{2}x}={\sec }^{2}x$	${\left[f\left(x\right)\right]}^n\left(n\in \mathbb{R}\right)$	$n{\left[f\left(x\right)\right]}^{n-1}{f}^{\prime }\left(x\right)$
$\cot x\left(x\ne k\pi ,k\in \mathbb{Z}\right)$	$\frac{-1}{{\sin }^{2}x}=-{\mathrm{cosec}}^{2}x$	$\ln f\left(x\right)\left(f\left(x\right)>0\right)$	$\frac{f^{\prime }\left(x\right)}{f\left(x\right)}$

注 事实上, 为了便于微分, 可以把函数转化成一种更简单的形式, 如变成不含括号的和式 (参见第 13 页 1.1.6.1)、分离出表达式的整有理部分 (参见第 17 页 1.1.7) 或取表达式的对数 (参见第 10 页 1.1.4.3).

$◼\mathbf{A}$: $y=\frac{2-3\sqrt{x}+4\sqrt[3]{x}+x^2}{x}=\frac{2}{x}-3x^{-\frac{1}{2}}+4x^{-\frac{2}{3}}+x;$

$$\frac{\mathrm{d}y}{\mathrm{d}x}=-2x^{-2}+\frac{3}{2}{x}^{-\frac{3}{2}}-\frac{8}{3}{x}^{-\frac{5}{3}}+1$$

$◼\mathbf{B}$: $y=\ln \sqrt{\frac{x^2+1}{x^2-1}}=\frac{1}{2}\ln \left(x^2+1\right)-\frac{1}{2}\ln \left(x^2-1\right);$

$$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{1}{2}\left(\frac{2x}{x^2+1}\right)-\frac{1}{2}\left(\frac{2x}{x^2-1}\right)=-\frac{2x}{x^4-1}.$$

6.1.2.2 微分基本法则

设 $u,v,w,y$ 是变量 $x$ 的函数, $u^{\prime },v^{\prime },w^{\prime },y^{\prime }$ 是关于 $x$ 的导数,其微分记为 $\mathrm{d}u,\mathrm{d}v,\mathrm{d}w,\mathrm{d}y$ (参见第 599 页 6.2.1.3). 表 6.2 总结了微分基本法则,下面逐一说明.

1. 常函数的导数

常函数 $c$ 的导数为 0,即

$$\begin{array}{}\text{(6.4)}& c^{\prime }=0\text{.}\end{array}$$

2. 数乘函数的导数

常因子 $c$ 可从微分符号中分解出来,即

$$\begin{array}{}\text{(6.5)}& {\left(cu\right)}^{\prime }=c{u}^{\prime },\mathrm{d}\left(cu\right)=c\mathrm{d}u.\end{array}$$

3. 和的导数

若函数 $u,v,w$ 等均可微,它们的和或差也可微,且等于微分的和或差,即

$$\begin{array}{}\text{(6.6a)}& {(u+v-w)}^{\prime }=u^{\prime }+v^{\prime }-w^{\prime },\end{array}$$$$\begin{array}{}\text{(6.6b)}& \mathrm{d}\left(u+v-w\right)=\mathrm{d}u+\mathrm{d}v-\mathrm{d}w.\end{array}$$

可能每个被加式都不可微, 但它们的和或差可微, 此时其导数必须用定义中的公式 (6.1) 来计算.

4. 乘积的导数

若两个、三个或 $n$ 个函数均可微,则它们的乘积也可微,且通过如下法则来计算:

a) 两函数乘积的导数

$$\begin{array}{}\text{(6.7a)}& {\left(uv\right)}^{\prime }=u^{\prime }v+u{v}^{\prime },\mathrm{d}\left(uv\right)=v\mathrm{d}u+u\mathrm{d}v.\end{array}$$

可能每项都不可微, 但它们的乘积可微, 此时其导数必须用定义中的公式 (6.1) 来计算.

b) 三个函数乘积的导数

$$\begin{array}{}\text{(6.7b)}& {\left(uvw\right)}^{\prime }=u^{\prime }vw+u{v}^{\prime }w+uv{w}^{\prime },\mathrm{d}\left(uvw\right)=vw\mathrm{d}u+uw\mathrm{d}v+uv\mathrm{d}w.\end{array}$$

表达式	求导数公式
常函数	$c^{\prime }=0\left(c\text{为常数}\right)$
常数倍	${\left(cu\right)}^{\prime }=c{u}^{\prime }\left(c\text{为常数}\right)$
和	${(u\pm v)}^{\prime }=u^{\prime }\pm v^{\prime }$
两函数乘积	${\left(uv\right)}^{\prime }=u^{\prime }v+u{v}^{\prime }$
$n$ 个函数的乘积	${(u_1{u}_2\cdots u_n)}^{\prime }=\sum _{i=1}^n{u}_1\cdots u_i^{\prime }\cdots u_n$
商	${\left(\frac{u}{v}\right)}^{\prime }=\frac{v{u}^{\prime }-u{v}^{\prime }}{v^2}\left(v\ne 0\right)$
两函数的链式法则	$y=u\left(v\left(x\right)\right):y^{\prime }=\frac{\mathrm{d}u}{\mathrm{d}v}\frac{\mathrm{d}v}{\mathrm{d}x}$
三个函数的链式法则	$y=u\left(v\left(w\left(x\right)\right)\right):y^{\prime }=\frac{\mathrm{d}u}{\mathrm{d}v}\frac{\mathrm{d}v}{\mathrm{d}w}\frac{\mathrm{d}w}{\mathrm{d}x}$
幂	${\left(u^{\alpha }\right)}^{\prime }=\alpha u^{\alpha -1}{u}^{\prime }$ $\left(\alpha \in \mathbb{R},\alpha \ne 0\right)$ 特别地, ${\left(\frac{1}{u}\right)}^{\prime }=-\frac{u^{\prime }}{u^2}$
对数微分	$\frac{\mathrm{d}\left(\ln y\left(x\right)\right)}{\mathrm{d}x}=\frac{1}{y}{y}^{\prime }\Rightarrow y^{\prime }=y\frac{\mathrm{d}\left(\ln y\right)}{\mathrm{d}x}$ 特别地, ${\left(u^v\right)}^{\prime }=u^v\left(v^{\prime }\ln u+\frac{v{u}^{\prime }}{u}\right)(u>$
反函数可微分	设 $\phi$ 为 $f$ 的反函数,即 $y=f\left(x\right)\iff x=\phi \left(y\right)$ ,有 $f^{\prime }\left(x\right)=\frac{1}{{\phi }^{\prime }\left(y\right)}$
隐函数微分	$F\left(x,y\right)=0$ : $F_x+F_y{y}^{\prime }=0$ 或 $y^{\prime }=-\frac{F_x}{F_y}$$\left(F_x=\frac{\partial F}{\partial x},F_y=\frac{\partial F}{\partial y};F_y\ne 0\right)$
参数形式函数可微分	( $t$ 为参数): $y^{\prime }=\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\dot{y}}{\dot{x}}\left(\dot{x}=\frac{\mathrm{d}x}{\mathrm{d}t},\dot{y}=\frac{\mathrm{d}y}{\mathrm{d}t}\right)$
极坐标形式函数可微分	$x=\rho \left(\phi \right)\cos \phi$ (角 $\phi$ 为参数) $y=\rho \left(\phi \right)\sin \phi$ $y^{\prime }=\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\dot{\rho }\sin \phi +\rho \cos \phi }{\dot{\rho }\cos \phi -\rho \sin \phi }$$\left(\dot{\rho }=\frac{\mathrm{d}\rho }{\mathrm{d}\phi }\right)$

c) $n$ 个函数乘积的导数

$$\begin{array}{}\text{(6.7c)}& {(u_1{u}_2\cdots u_n)}^{\prime }=\sum _{i=1}^n{u}_1{u}_2\cdots u_i^{\prime }\cdots u_n.\end{array}$$

$◼\mathbf{A}$: $y=x^3\cos x,y^{\prime }=3x^2\cos x-x^3\sin x$ .

$◼\mathbf{B}$: $y=x^3{\mathrm{e}}^x\cos x,y^{\prime }=3x^2{\mathrm{e}}^x\cos x+x^3{\mathrm{e}}^x\cos x-x^3{\mathrm{e}}^x\sin x$ .

5. 商的导数

若 $u,v$ 均可微,且 $v\left(x\right)\ne 0$ ,则它们的比也可微,有

$$\begin{array}{}\text{(6.8)}& {\left(\frac{u}{v}\right)}^{\prime }=\frac{v{u}^{\prime }-u{v}^{\prime }}{v^2},\mathrm{d}\left(\frac{u}{v}\right)=\frac{v\mathrm{d}u-u\mathrm{d}v}{v^2}\end{array}$$

$y=\tan x=\frac{\sin x}{\cos x},y^{\prime }=\frac{\left(\cos x\right){(\sin x)}^{\prime }-\left(\sin x\right){(\cos x)}^{\prime }}{{\cos }^{2}x}=\frac{{\cos }^{2}x+{\sin }^{2}x}{{\cos }^{2}x}=$ $\frac{1}{{\cos }^{2}x}$

6. 链式法则

复合函数 (参见第 77 页2.1.5.5,2.) $y=u\left(v\left(x\right)\right)$ 的导数

$$\begin{array}{}\text{(6.9)}& \frac{\mathrm{d}y}{\mathrm{d}x}=u^{\prime }\left(v\right)v^{\prime }\left(x\right)=\frac{\mathrm{d}u}{\mathrm{d}v}\frac{\mathrm{d}v}{\mathrm{d}x},\end{array}$$

其中函数 $u=u\left(v\right)$ 和 $v=v\left(x\right)$ 均为关于其自变量的可微函数. $u\left(v\right)$ 称为外函数, $v\left(x\right)$ 称为内函数,由此 $\frac{\mathrm{d}u}{\mathrm{d}v}$ 是外导数, $\frac{\mathrm{d}v}{\mathrm{d}x}$ 是内导数. 可能函数 $u,v$ 均不可微,但复合函数可微, 此时要利用定义中的公式 (6.1) 求导.

类似地, 若存在更长的 “链式”, 即复合函数有多个中间变量, 我们必须继续进行计算. 例如,当 $y=u\left(v\left(w\left(x\right)\right)\right)$ 时,

$$\begin{array}{}\text{(6.10)}& y^{\prime }=\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}u}{\mathrm{d}v}\frac{\mathrm{d}v}{\mathrm{d}w}\frac{\mathrm{d}w}{\mathrm{d}x}.\end{array}$$

$◼\mathbf{A}$: $y={\mathrm{e}}^{{\sin }^{2}x},\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}\left({\mathrm{e}}^{{\sin }^{2}x}\right)}{\mathrm{d}\left({\sin }^{2}x\right)}\frac{\mathrm{d}\left({\sin }^{2}x\right)}{\mathrm{d}\left(\sin x\right)}\frac{\mathrm{d}\left(\sin x\right)}{\mathrm{d}x}={\mathrm{e}}^{{\sin }^{2}x}2\sin x\cos x$ .

$◼\mathbf{B}$: $y={\mathrm{e}}^{\tan \sqrt{x}};\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}\left({\mathrm{e}}^{\tan \sqrt{x}}\right)}{\mathrm{d}\left(\tan \sqrt{x}\right)}\frac{\mathrm{d}\left(\tan \sqrt{x}\right)}{\mathrm{d}\left(\sqrt{x}\right)}\frac{\mathrm{d}\left(\sqrt{x}\right)}{\mathrm{d}x}={\mathrm{e}}^{\tan \sqrt{x}}\frac{1}{{\cos }^2\sqrt{x}}\frac{1}{2\sqrt{x}}.$

7. 对数微分法

若 $y\left(x\right)>0$ ,可由函数 $\ln y\left(x\right)$ 计算 $y^{\prime }$ ,(利用链式法则) 有

$$\begin{array}{}\text{(6.11)}& \frac{\mathrm{d}\left(\ln y\left(x\right)\right)}{\mathrm{d}x}=\frac{1}{y\left(x\right)}{y}^{\prime }.\end{array}$$

由此,

$$\begin{array}{}\text{(6.12)}& y^{\prime }=y\left(x\right)\frac{\mathrm{d}\left(\ln y\left(x\right)\right)}{\mathrm{d}x}.\end{array}$$

注 1 借助对数微分, 某些微分问题可能得到简化, 对有些函数而言, 对数求导法是计算其导数的唯一方法, 例如, 若函数具有如下形式:

$$\begin{array}{}\text{(6.13)}& y=u{\left(x\right)}^{v\left(x\right)},\text{ 其中 }u\left(x\right)>0,\end{array}$$

由公式 (6.12), 这个方程的对数导数

$$\begin{array}{}\text{(6.14)}& y^{\prime }=y\frac{\mathrm{d}\left(\ln u^v\right)}{\mathrm{d}x}=y\frac{\mathrm{d}\left(v\ln u\right)}{\mathrm{d}x}=u^v\left(v^{\prime }\ln u+\frac{v{u}^{\prime }}{u}\right),\end{array}$$$$y={(2x+1)}^{3x},\ln y=3x\ln \left(2x+1\right),\frac{y^{\prime }}{y}=3\ln \left(2x+1\right)+\frac{3x\cdot 2}{2x+1};$$$$y^{\prime }=3{(2x+1)}^{3x}\left(\ln \left(2x+1\right)+\frac{2x}{2x+1}\right).$$

注 2 当求几个函数乘积的导数时, 常常使用对数求导法.

$◼\mathbf{A}$: $y=\sqrt{x^3{\mathrm{e}}^{4x}\sin x},\ln y=\frac{1}{2}\left(3\ln x+4x+\ln \sin x\right)$ ,

$$\frac{y^{\prime }}{y}=\frac{1}{2}\left(\frac{3}{x}+4+\frac{\cos x}{\sin x}\right),y^{\prime }=\frac{1}{2}\sqrt{x^3{\mathrm{e}}^{4x}\sin x}\left(\frac{3}{x}+4+\cot x\right).$$

$◼\mathbf{B}$: $y=uv,\ln y=\ln u+\ln v,\frac{y^{\prime }}{y}=\frac{1}{u}{u}^{\prime }+\frac{1}{v}{v}^{\prime }$ ,故有 $y^{\prime }={\left(uv\right)}^{\prime }=v{u}^{\prime }+u{v}^{\prime }$ ,因此可得乘积的导数公式(6.7a)(假设 $u,v>0$ ).

$◼\mathbf{C}$: $y=\frac{u}{v},\ln y=\ln u-\ln v,\frac{y^{\prime }}{y}=\frac{1}{u}{u}^{\prime }-\frac{1}{v}{v}^{\prime }$ ,故有 $y^{\prime }={\left(\frac{u}{v}\right)}^{\prime }=\frac{u^{\prime }}{v}-\frac{u{v}^{\prime }}{v^2}=$ $\frac{u^{\prime }v-u{v}^{\prime }}{v^2}$ ,因此可得商的导数公式 (6.8)(假设 $u,v>0$ ).

8. 反函数的导数

若 $y=\phi \left(x\right)$ 是原函数 $y=f\left(x\right)$ 的反函数,则 $y=f\left(x\right)$ 与 $x=\phi \left(y\right)$ 等价. 对每组对应的值 $x$ 和 $y$ ,满足 $f$ 关于 $x$ 可微,且 $\phi$ 关于 $y$ 可微,当每个导数都不等于 0 时,则 $f$ 的导数与反函数 $\phi$ 的导数之间具有关系:

$$\begin{array}{}\text{(6.15)}& f^{\prime }\left(x\right)=\frac{1}{{\phi }^{\prime }\left(y\right)}\text{ 或 }\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{1}{\frac{\mathrm{d}x}{\mathrm{d}y}}.\end{array}$$

$◼$ 当 $-1<x<1$ 时,函数 $y=f\left(x\right)=\arcsin x$ 与 $-\frac{\pi }{2}<y<\frac{\pi }{2}$ 时的函数 $x=$ $\phi \left(y\right)=\sin y$ 等价. 因为当 $-\frac{\pi }{2}<y<\frac{\pi }{2}$ 时, $\cos y\ne 0$ ,故由 (6.15),有

$${(\arcsin x)}^{\prime }=\frac{1}{{(\sin y)}^{\prime }}=\frac{1}{\cos y}=\frac{1}{\sqrt{1-{\sin }^{2}y}}=\frac{1}{\sqrt{1-x^2}}.$$

9. 隐函数的导数

设函数 $y=f\left(x\right)$ 由隐函数方程 $F\left(x,y\right)$ 给出,利用多元函数微分法 (参见第 598 页 6.2),计算关于 $x$ 的导数. 若偏导数 $f=F_y\ne 0$ ,有

$$\begin{array}{}\text{(6.16)}& \frac{\partial F}{\partial x}+\frac{\partial F}{\partial y}{y}^{\prime }=0,\text{ 故 }{y}^{\prime }=-\frac{F_x}{F_y}.\end{array}$$

$◼$ 半轴长为 $a$ 和 $b$ 的椭圆方程 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ 的隐函数形式为 $F\left(x,y\right)=\frac{x^2}{a^2}+\frac{y^2}{b^2}-1=$ 0 . 由 (6.16),在椭圆上的点(x, y)处,切线的斜率

$$y^{\prime }=-\frac{2x}{a^2}/\frac{2y}{b^2}=-\frac{b^2}{a^2}\frac{x}{y}.$$

10. 参数形式的函数的导数

若函数 $y=f\left(x\right)$ 的参数方程为 $x=x\left(t\right),y=y\left(t\right)$ ,则导数 $y^{\prime }$ 计算公式如下:

$$\begin{array}{}\text{(6.17)}& \frac{\mathrm{d}y}{\mathrm{d}x}=f^{\prime }\left(x\right)=\frac{\dot{y}}{\dot{x}},\end{array}$$

其中 $\dot{y}\left(t\right)=\frac{\mathrm{d}y}{\mathrm{d}t},\dot{x}\left(t\right)=\frac{\mathrm{d}x}{\mathrm{d}t}$ ,且 $\dot{x}\left(t\right)\ne 0$ .

$◼$ 极坐标表示: 若函数由极坐标(参见第 257 页 3.5.2.2,3.) $\rho =\rho \left(\phi \right)$ 给出,则其参数形式为

$$\begin{array}{}\text{(6.18)}& x=\rho \left(\phi \right)\cos \phi ,y=\rho \left(\phi \right)\sin \phi ,\end{array}$$

其中角 $\phi$ 为参数,由 (6.17),曲线切线的斜率 (参见第 327 页 3.6.1.2,2. 或 581 页6.1.1,2.)

$$\begin{array}{}\text{(6.19)}& y^{\prime }=\frac{\dot{\rho }\sin \phi +\rho \cos \phi }{\dot{\rho }\cos \phi -\rho \sin \phi },\text{ 其中 }\dot{\rho }=\frac{\mathrm{d}\rho }{\mathrm{d}\phi }.\end{array}$$

注 (1) 导数 $\dot{x},\dot{y}$ 是曲线在点 $\left(x\left(t\right),y\left(t\right)\right)$ 处切向量的分量.

(2)常常要用到复关系:

$$\begin{array}{}\text{(6.20)}& x\left(t\right)+\mathrm{i}y\left(t\right)=z\left(t\right),\dot{x}\left(t\right)+\mathrm{i}\dot{y}\left(t\right)=\dot{z}\left(t\right).\end{array}$$

圆周运动: $z\left(t\right)=r{\mathrm{e}}^{\mathrm{i}wt}\left(r,w\text{为常数}\right),\dot{z}\left(t\right)=r\mathrm{i}w{\mathrm{e}}^{\mathrm{i}wt}=rw{\mathrm{e}}^{\mathrm{i}\left(wt+\frac{\pi }{2}\right)}$ . 切向量在相对于位置向量前向位移 $\pi /2$ 处转动.

11. 图解微分法

若可微函数 $y=f\left(x\right)$ 可用笛卡儿坐标系中区间(a, b)上的曲线 $\mathrm{\Gamma }$ 来表示,则它的导数曲线 ${\mathrm{\Gamma }}^{\prime }$ 可以近似地构造出来. 虽然仅凭肉眼估计的切线结构准确率相当低,但如果切线 $MN$ 的方向已知 (图 6.4),便可以更精确地确定出切点 $A$ .

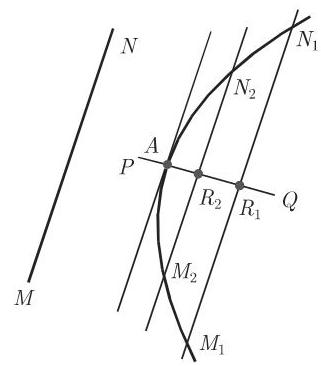
(1) 切线切点的构造.

首先作平行于切线方向 $MN$ 的两条割线 $\overline{M_1{N}_1},\overline{M_2{N}_2}$ ,满足曲线在相距不远处与之相交. 接着确定出割线的中点,过中点作一条直线 $PQ$ ,并与曲线交于点 $A$ , 这就是切线方向为 $MN$ 时切点的近似点. 为了检查其正确性,可以在靠近前两条割线的位置再作一条平行线,直线 $PQ$ 将与其在中点处相交.

(2)导数曲线的构造.

a) 选择某些方向 $l_1,l_2,\cdots ,l_n$ ,使之为图 6.5 中曲线 $y=f\left(x\right)$ 在其定义域内的某些切线方向,并确定出相应的切点 $A_1,A_2,\cdots ,A_n$ ,其中切线不必构造出来.

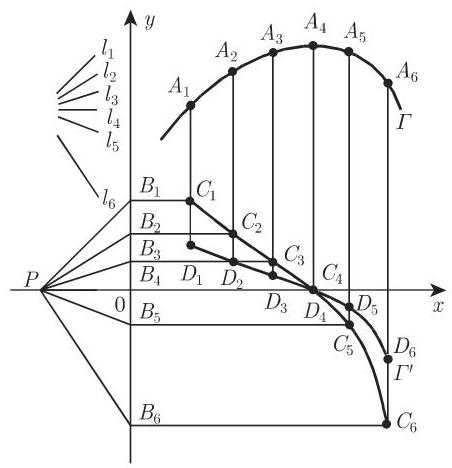
b) 在 $x$ 轴的负半轴上选择一点 $P$ 作为 “极点”,线段 $PO=a$ 越长曲线越平缓.

c) 过顶点 $P$ 作平行于 $l_1,l_2,\cdots ,l_n$ 的直线,与 $y$ 轴的交点记为 $B_1,B_2,\cdots ,B_n$ .

d) 从 $A_1,A_2,\cdots ,A_n$ 引垂线,交过 $B_1,B_2,\cdots ,B_n$ 的水平线为 $C_1,C_2,\cdots ,C_n$ , 得 $B_1{C}_1,B_2{C}_2,\cdots ,B_n{C}_n$ .

e) 用曲线尺连接点 $C_1,C_2,\cdots ,C_n$ ,得到的曲线满足方程 $y=a{f}^{\prime }\left(x\right)$ . 若线段 $a$ 正好等于 $y$ 轴的单位长度,则得到的曲线是导数曲线. 否则,必须把 $C_1,C_2,\cdots ,C_n$ 的每个坐标乘上因子 $1/a$ . 图 6.5 中的点 $D_1,D_2,\cdots ,D_n$ 位于导数的精确标度曲线 ${\mathrm{\Gamma }}^{\prime }$ 上.