3.3.4 由曲面所界的立体

在这一节中我们将使用以下记号: $V$ 为体积, $S$ 为表面积, $M$ 为侧面积, $h$ 为高, $A_G$ 为底面积.

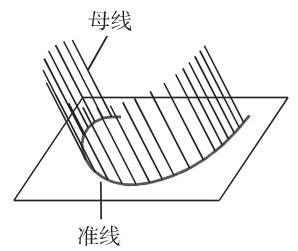
(1)柱面 可以通过一条直线,即母线沿一条曲线,即所谓准线平移得到 (图 3.64).

(2)柱体 是由具有一条封闭准线的柱面和该柱面从两个平行平面截出的两个平行的底所界的立体. 对于每个底的周长为 $p$ ,垂直于母线的横截面周长为 $s$ ,面积为 $Q$ ,母线长为 $l$ 的任意柱体 (图 3.65),以下公式成立:

$$\begin{array}{}\text{(3.137)}& V=A_{G}h=Ql,\end{array}$$$$\begin{array}{}\text{(3.138)}& M=ph=sl.\end{array}$$

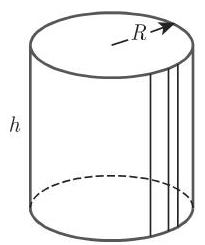
(3) 直圆柱 以圆作为底并且其母线垂直于圆面 (图 3.66). 设底半径为 $R$ ,则有

$$\begin{array}{}\text{(3.139)}& V=\pi R^{2}h\end{array}$$$$\begin{array}{}\text{(3.140)}& M=2\pi Rh,\end{array}$$$$\begin{array}{}\text{(3.141)}& S=2\pi R\left(R+h\right).\end{array}$$

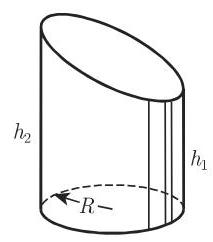
(4) 斜截圆柱(图 3.67)

$$\begin{array}{}\text{(3.142)}& V=\pi R^2\frac{h_1+h_2}{2},\end{array}$$$$\begin{array}{}\text{(3.143)}& M=\pi R\left(h_1+h_2\right),\end{array}$$$$\begin{array}{}\text{(3.144)}& S=\pi R\left[h_1+h_2+R+\sqrt{R^2+{\left(\frac{h_2-h_1}{2}\right)}^2}\right].\end{array}$$

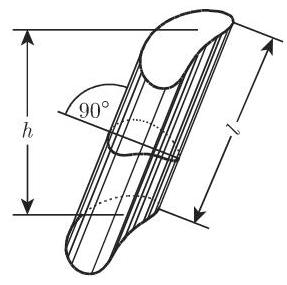
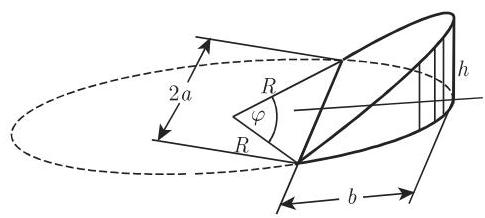
(5) 柱段 应用图 3.68 的记号,设 $\alpha =\phi /2$ 并以弧度记,则有

$$V=\frac{h}{3b}\left[a\left(3R^2-a^2\right)+3R^2\left(b-R\right)\alpha \right]$$$$\begin{array}{}\text{(3.145)}& =\frac{h{R}^3}{b}\left(\sin \alpha -\frac{{\sin }^3\alpha }{3}-\alpha \cos \alpha \right),\end{array}$$$$\begin{array}{}\text{(3.146)}& M=\frac{2Rh}{b}\left[\left(b-R\right)\alpha +a\right],\end{array}$$

其中当 $b>R,\phi >\pi$ 时公式仍成立.

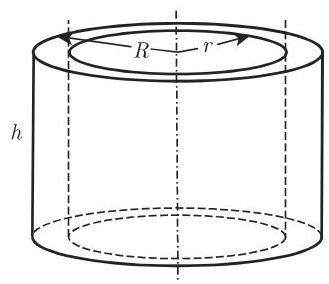
(6) 空心圆柱 应用记号 $R$ 表示外半径, $r$ 表示内半径, $\delta =R-r$ 表示两半径之差, $\rho =\frac{R+r}{2}$ 表示两半径的平均值 (图 3.69),则有

$$\begin{array}{}\text{(3.147)}& V=\pi h\left(R^2-r^2\right)=\pi h\delta \left(2R-\delta \right)=\pi h\delta \left(2r+\delta \right)=2\pi h\delta \varrho .\end{array}$$

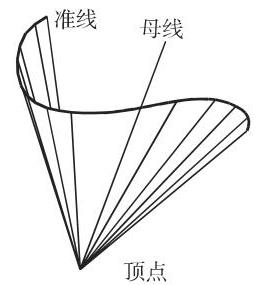
(7) 锥面 是由一条直线, 即母线沿一条曲线, 即准线移动使得该直线总是通过一个定点, 即顶点而产生的 (图 3.70).

(8) 锥(图 3.71) 是由具有一条封闭准线的锥面和该锥面从一个平面截出的底所界的立体. 对于任意一个锥, 则有

$$\begin{array}{}\text{(3.148)}& V=\frac{h{A}_G}{3}.\end{array}$$

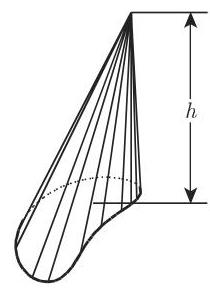
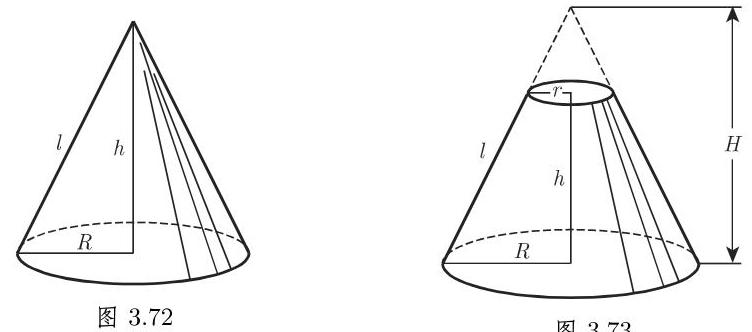
(9) 直圆锥 以圆作为底而其顶点在该圆上方正对着圆心 (图 3.72). 以 $l$ 表示母线长, $R$ 表示底圆半径,则有

$$\begin{array}{}\text{(3.149)}& V=\frac{1}{3}\pi R^{2}h\end{array}$$$$\begin{array}{}\text{(3.150)}& M=\pi Rl=\pi R\sqrt{R^2+h^2},\end{array}$$$$\begin{array}{}\text{(3.151)}& S=\pi R\left(R+l\right).\end{array}$$

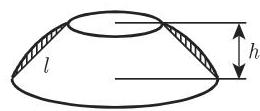
(10) 直锥台或截锥(图 3.73)

$$\begin{array}{}\text{(3.152)}& l=\sqrt{h^2+{(R-r)}^2},\end{array}$$$$\begin{array}{}\text{(3.153)}& M=\pi l\left(R+r\right),\end{array}$$$$\begin{array}{}\text{(3.154)}& V=\frac{\pi h}{3}\left(R^2+r^2+Rr\right),\end{array}$$$$\begin{array}{}\text{(3.155)}& H=h+\frac{hr}{R-r}.\end{array}$$

(11) 圆锥截面 参见第 277 页 3.5.2.11.

(12) 球 (图 3.74) 具有半径 $R$ 和直径 $D=2R$ . 其与任一平面的截线都是圆. 过球心的平面产生的截线是半径为 $R$ 的大圆 (参见第 213 页 3.4.1.1). 如果球面上的两个点不是同一条直径的端点, 那么只能有一个大圆适合通过它们. 球面上两点在球面上的最短连线是它们之间的大圆弧 (参见第 213 页 3.4.1.1).

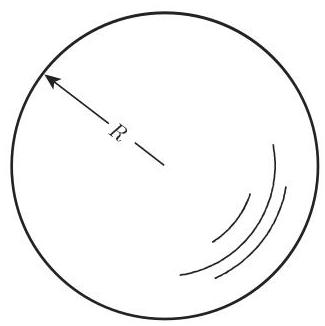
涉及球的表面积和体积的公式如下:

$$\begin{array}{}\text{(3.156a)}& S=4\pi R^2\approx 12.57R^2,\end{array}$$$$\begin{array}{}\text{(3.156b)}& S=\pi D^2\approx 3.142D^2,\end{array}$$$$\begin{array}{}\text{(3.156c)}& S=\sqrt[3]{36\pi V^2}\approx 4.836\sqrt[3]{V^2},\end{array}$$$$\begin{array}{}\text{(3.157a)}& V=\frac{4}{3}\pi R^3\approx 4.189R^3,\end{array}$$$$\begin{array}{}\text{(3.157b)}& V=\frac{\pi D^3}{6}\approx 0.5236D^3,\end{array}$$$$\begin{array}{}\text{(3.157c)}& V=\frac{1}{6}\sqrt{\frac{S^3}{\pi }}\approx 0.09403\sqrt{S^3},\end{array}$$$$\begin{array}{}\text{(3.158a)}& R=\frac{1}{2}\sqrt{\frac{S}{\pi }}\approx 0.2821\sqrt{S},\end{array}$$$$\begin{array}{}\text{(3.158b)}& R=\sqrt[3]{\frac{3V}{4\pi }}\approx 0.6204\sqrt[3]{V}.\end{array}$$

(13) 球心角体(图 3.75)

$$\begin{array}{}\text{(3.159)}& S=\pi R\left(2h+a\right),\end{array}$$$$\begin{array}{}\text{(3.160)}& V=\frac{2\pi R^{2}h}{3}.\end{array}$$

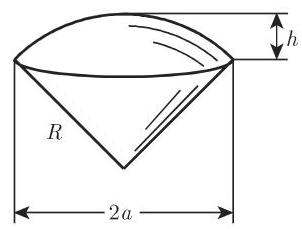
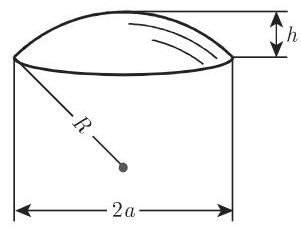
(14) 球冠(图 3.76)

$$\begin{array}{}\text{(3.161)}& a^2=h\left(2R-h\right),\end{array}$$$$\begin{array}{}\text{(3.162)}& V=\frac{1}{6}\pi h\left(3a^2+h^2\right)=\frac{1}{3}\pi h^2\left(3R-h\right),\end{array}$$$$\begin{array}{}\text{(3.163)}& M=2\pi Rh=\pi \left(a^2+h^2\right),\end{array}$$$$\begin{array}{}\text{(3.164)}& S=\pi \left(2Rh+a^2\right)=\pi \left(h^2+2a^2\right).\end{array}$$

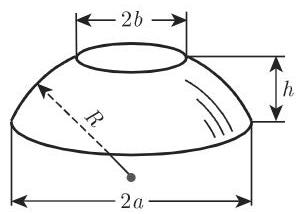
(15) 球层(图 3.77)

$$\begin{array}{}\text{(3.165)}& R^2=a^2+{\left(\frac{a^2-b^2-h^2}{2h}\right)}^2,\end{array}$$$$\begin{array}{}\text{(3.166)}& V=\frac{1}{6}\pi h\left(3a^2+3b^2+h^2\right),\end{array}$$$$\begin{array}{}\text{(3.167)}& M=2\pi Rh,\end{array}$$$$\begin{array}{}\text{(3.168)}& S=\pi \left(2Rh+a^2+b^2\right).\end{array}$$

如果 $V_1$ 是内接于球层的截锥 (图 3.78) 的体积, $l$ 是它的母线长,则有

$$\begin{array}{}\text{(3.169)}& V-V_1=\frac{1}{6}\pi h{l}^2.\end{array}$$

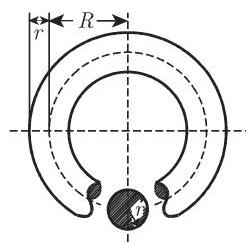
(16) 环面(图 3.79) 是一个圆绕位于它所在平面且不与该圆相交的一个轴旋转产生的立体.

$$\begin{array}{}\text{(3.170a)}& S=4{\pi }^{2}Rr\approx 39.48Rr,\end{array}$$$$\begin{array}{}\text{(3.170b)}& S={\pi }^{2}Dd\approx 9.870Dd,\end{array}$$$$\begin{array}{}\text{(3.171a)}& V=2{\pi }^{2}R{r}^2\approx 19.74R{r}^2,\end{array}$$$$\begin{array}{}\text{(3.171b)}& V=\frac{1}{4}{\pi }^{2}D{d}^2\approx 2.467D{d}^2.\end{array}$$

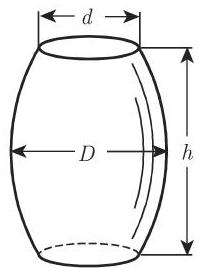
(17) 桶状体(图 3.80) 由母曲线旋转产生; 圆桶状体是由圆弧旋转形成的, 抛物桶状体是由抛物线段旋转形成的. 对于圆桶状体有下列近似公式成立:

$$\begin{array}{}\text{(3.172a)}& V\approx 0.262h\left(2D^2+d^2\right)\end{array}$$

或

$$\begin{array}{}\text{(3.172b)}& V\approx 0.0873h{(2D+d)}^2,\end{array}$$

而对于抛物桶状体, 则有

$$\begin{array}{}\text{(3.173)}& V=\frac{\pi h}{15}\left(2D^2+Dd+\frac{3}{4}{d}^2\right)\approx 0.05236h\left(8D^2+4Dd+3d^2\right).\end{array}$$