14.2.3 柯西积分公式

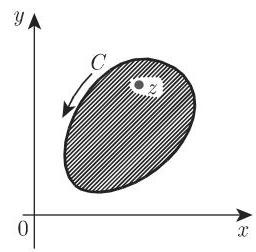
14.2.3.1 在一个区域内点集上的解析函数

如果 $f\left(z\right)$ 在一条简单闭曲线 $C$ 以及它内部的单连通区域上是解析的,那么对于该单连通区域的每个内点 $z$ (图 14.37),下述表达式成立:

$$\begin{array}{}\text{(14.42)}& f\left(z\right)=\frac{1}{2\pi \mathrm{i}}{\oint }_C\frac{f\left(\zeta \right)}{\zeta -z}\mathrm{d}\zeta \text{ (柯西积分公式),}\end{array}$$

其中 $\zeta$ 逆时针地走过曲线 $C$ . 利用这个公式,解析函数在一个区域内部的值被该函数在区域边界上的值所表示. 从 (14.42) 即得该函数的 $n$ 次导数的存在性以及其积分表达式在区域 $G$ 上是解析的:

$$\begin{array}{}\text{(14.43)}& f^{\left(n\right)}\left(z\right)=\frac{n!}{2\pi \mathrm{i}}{\oint }_C\frac{f\left(\zeta \right)}{{(\zeta -z)}^{n+1}}\mathrm{d}\zeta .\end{array}$$

因而, 如果一个复函数是可微的, 即, 它是解析的, 那么它是无穷多次可微的. 与此相反, 在实数的情形, 可微性并不包含反复的可微性.

方程 (14.42) 和 (14.43) 被称为柯西积分公式 (Cauchy integral formulas).

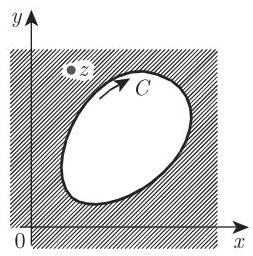
14.2.3.2 在一个区域外点集上的解析函数

如果一个函数 $f\left(z\right)$ 在平面上一条闭积分曲线 $C$ 的整个外部是解析的,那么函数 $f\left(z\right)$ 在此外部区域中的一点 $z$ 处的值及其各阶导数的值可以用相同的柯西公式 (14.42),(14.43) 来给出,但是曲线 $C$ 现在是顺时针方向 (图 14.38). 借助于柯西积分公式还可以计算某些实积分 (参见第 984 页 14.4).