2.17.2 坐标纸

最常用的坐标纸是通过把直角坐标系的坐标轴用标度方程

$$\begin{array}{}\text{(2.269)}& x=l_1\left[g\left(u\right)-g\left(u_0\right)\right],y=l_2\left[f\left(v\right)-f\left(v_0\right)\right]\end{array}$$

标准化后得到的. 其中 $l_1,l_2$ 为标度因子, $u_0,v_0$ 为标度的初始点.

2.17.2.1 半对数坐标纸

若对 $x$ 轴进行等距划分,对 $y$ 轴进行对数划分,就得到半对数坐标纸或半对数坐标系.

标度方程

$x=l_1\left[u-u_0\right]$ (线性标度), $y=l_2\left[\lg v-\lg v_0\right]$ (对数标度).(2.270)

图 2.98 是半对数坐标纸的一个例子.

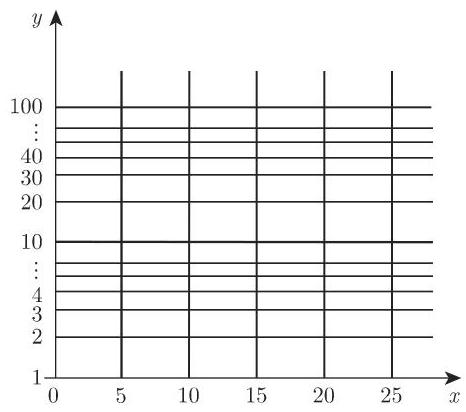
指数函数的表示 在半对数坐标纸上, 指数函数

$$\begin{array}{}\text{(2.271a)}& y=\alpha {\mathrm{e}}^{\beta x}\left(\alpha ,\beta \text{ 为常数 }\right)\end{array}$$

的图像为一直线 (参见第 143 页 2.16.2.2 中的修正). 可按如下方法利用该性质: 若半对数坐标纸上的测点大约位于一条直线上, 可假设这些变量的关系满足 (2.271a). 借助此直线,可目测确定 $\alpha ,\beta$ 的近似值. 事实上,考虑直线上的两点 $P_1\left(x_1,y_1\right)$ 和 $P_2\left(x_2,y_2\right)$ ,可得

$$\begin{array}{}\text{(2.271b)}& \beta =\frac{\ln y_2-\ln y_1}{x_2-x_1},\alpha =y_1{\mathrm{e}}^{\beta x_1}.\end{array}$$

2.17.2.2 双对数坐标纸

若直角坐标系的坐标轴 $x$ 轴和 $y$ 轴都是经过对数函数标准化后得到的,则称之为双对数坐标纸、重对数坐标纸或双对数坐标系.

标度方程

$$\begin{array}{}\text{(2.272)}& x=l_1\left[\lg u-\lg u_0\right],y=l_2\left[\lg v-\lg v_0\right],\end{array}$$

其中 $l_1,l_2$ 为标度因子, $u_0,v_0$ 为初始点.

幂函数的表示 (参见第 91 页 2.5.3) 双对数坐标纸与半对数坐标纸方法类似,只不过其 $x$ 轴也进行的是对数划分. 在此坐标系中,幂函数

$$\begin{array}{}\text{(2.273)}& y=\alpha x^{\beta }\left(\alpha ,\beta \text{ 为常数 }\right)\end{array}$$

的图像为一直线 (参见第 142 页 2.16.2.1 中幂函数的修正). 这一性质的使用方法与半对数坐标纸中的类似.

2.17.2.3 倒数标度的坐标纸

坐标轴的标度划分来自反比函数 (2.45)(参见第 85 页 2.4.1).

标度方程

$$\begin{array}{}\text{(2.274)}& x=l_1\left(u-u_0\right),y=l_2\left(\frac{a}{v}-\frac{a}{v_0}\right)\left(a\text{ 为常数 }\right),\end{array}$$

其中 $l_1,l_2$ 为标度因子, $u_0,v_0$ 为初始点.

$◼$ 化学反应中的浓度 在化学反应中,浓度可以表示成关于时间 $t$ 的函数 $c=c\left(t\right)$ , 对 $c$ ,有如下结果:

$t/\min$	5	10	20	40
$c\cdot {10}^3/\left(\mathrm{mol}/\mathrm{L}\right)$	15.53	11.26	7.27	4.25

假设该反应为二级反应, 即满足

$$\begin{array}{}\text{(2.275)}& c\left(t\right)=\frac{c_0}{1+c_{0}kt}\left(c_0,k\text{ 为常数 }\right),\end{array}$$

两边取倒数,得 $\frac{1}{c}=\frac{1}{c_0}+kt$ . 故此,若坐标纸选择对 $y$ 轴作倒数划分, $x$ 轴作线性划分,则方程 (2.275) 表示一条直线. 如 $y$ 轴的标度方程 $y=10\cdot \frac{1}{v}\mathrm{cm}$ .

由相应的图 2.99, 显然测点大约位于一条直线上, 即可认为假设的关系 (2.275) 成立.

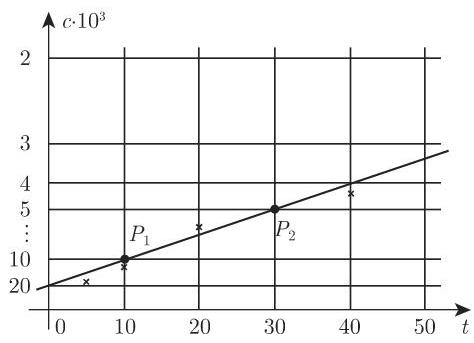
通过这些点,能确定参数 $k$ (反应速率) 和 $c_0$ (初始浓度) 的近似值. 如若选取两点 $P_1\left(10,10\right)$ 和 $P_2\left(30,5\right)$ ,有

$$k=\frac{1/c_1-1/c_2}{t_2-t_1}\approx 0.005,c_0\approx 20\cdot {10}^{-3}.$$

2.17.2.4 注

还有绘制和使用坐标纸的其他方法. 尽管当今每天仅凭实验室中得到的几个数据, 高速计算机便能分析出经验数据和测量结果, 但是坐标纸仍是用以说明函数关系和近似参数值最常用的方法, 而这些近似参数值正是采用数值方法所必须的初始值 (参见第 1282 页 19.6.2.4 中的非线性最小二乘法).