Appearance
16.2.4 连续分布
16.2.4.1 正态分布
1. 分布函数和密度函数
随机变量
是正态分布的密度函数,它在
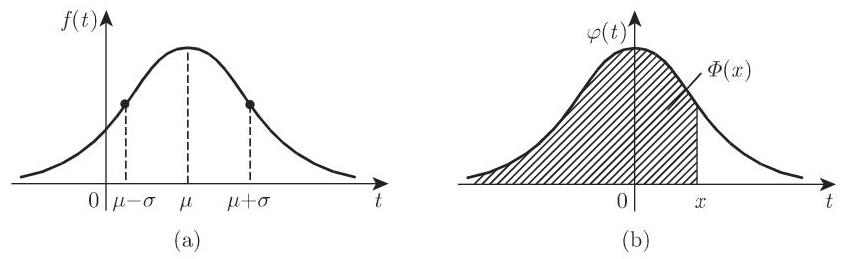
2. 期望和方差
正态分布的期望和方差分别是其参数
若随机变量
对 (16.70a) 式进行变量代换
16.2.4.2 标准正态分布、高斯误差函数
1. 分布函数和密度函数
在 (16.70a) 式中,当
其密度函数是
也称为高斯误差曲线(图 16.5(b)).
第 1458 页表 21.17 列出了标准正态分布函数
2. 概率积分
积分
其中 erf 表示误差函数.
16.2.4.3 对数正态分布
1. 密度函数和分布函数
称连续随机变量
定义的随机变量
其分布函数为
实际应用中主要使用自然对数或常用对数.
2. 期望和方差
使用自然对数可得到对数正态分布的期望和方差为
3. 注
a) 对数正态分布的密度函数处处连续, 且只对正的自变量取正值. 图 16.6 给出了
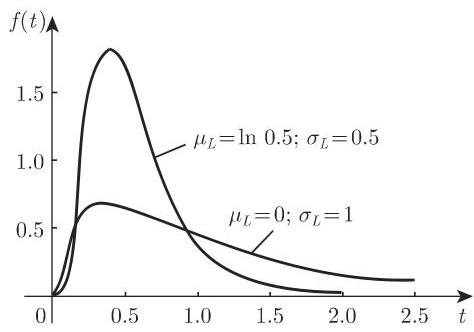
**b)
c) 对数正态分布的分布函数值
d) 对数正态分布经常应用于经济学、技术、生物过程中的寿命分析.
e) 正态分布可用于大量独立随机变量的加法叠加, 对数正态分布可用于大量独立随机变量的乘法叠加.
16.2.4.4 指数分布
1. 密度函数和分布函数
称连续随机变量
因此, 其分布函数为
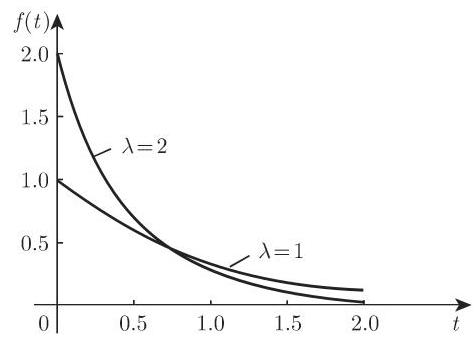
2. 期望和方差
下述问题常用指数分布描述: 电话的通话时间, 放射性粒子的寿命, 某些过程中机器在两次故障之间的工作时间, 灯泡或某建筑构件的寿命等.
16.2.4.5 韦布尔分布
1. 密度函数和分布函数
称连续随机变量
故其分布函数为
2. 期望和方差
此处,
在 (16.82a) 中,
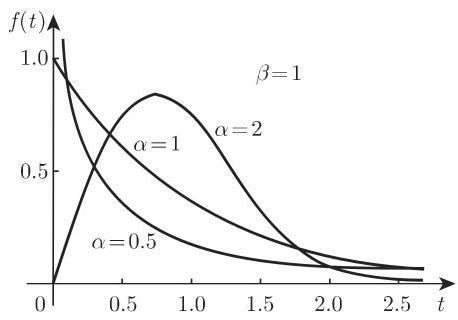
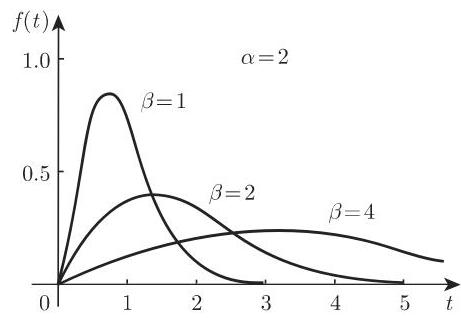
注 a) 当
b) 引入位置参数
c) 韦布尔分布在可靠性理论中特别有用, 比如它可以极灵活地描述建筑构件的系统寿命.
16.2.4.6
1. 密度函数和分布函数
设随机变量
的分布称为自由度
2. 期望和方差
3. 独立随机变量之和
若随机变量
4. 独立正态随机变量之和
如果随机变量
5. 分位数
对于自由度为
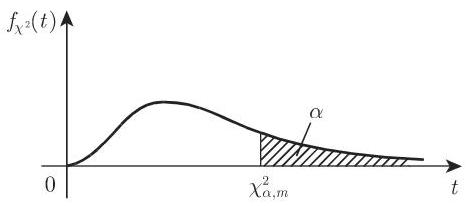
16.2.4.7 费希尔
1. 密度函数和分布函数
若随机变量
的分布是自由度为
(16.94a)
当
(16.94b)
2. 期望和方差
3. 分位数
对于费希尔分布 (图 16.11) 的分位数
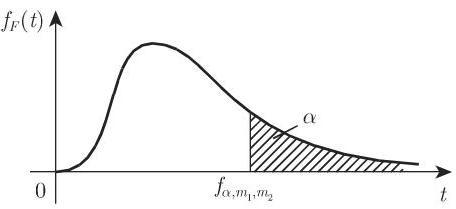
16.2.4.8
1. 密度函数和分布函数
如果随机变量
的分布称为自由度
(16.97b)
2. 期望和方差
3. 分位数
或
其数值由第 1463 页表 21.20 给出.
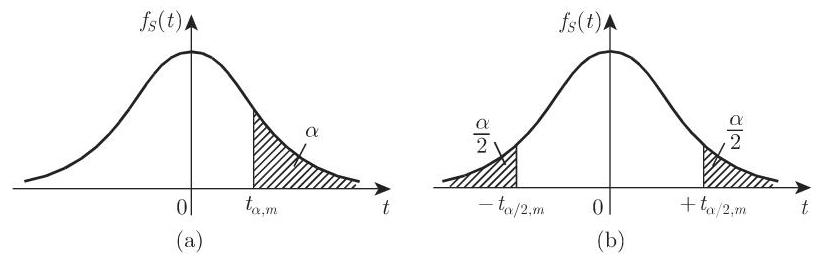
由戈赛特 (Gosset) 以笔名 “学生” 发表的