Appearance
3.5.1 向量代数
3.5.1.1 向量的定义
1. 标量和向量
取值为实数的量称为标量. 例如, 质量、温度、能量和功都是标量 (关于标量不变量, 参见第 247 页 3.5.1.5, 3., 第 287 页 3.5.3.4, 3. 和第 385 页 4.3.5.2, (2)).
空间中可以用大小和方向完全描述的量称为向量. 例如, 力、速度、加速度、角速度、角加速度以及电场和磁场强度都是向量. 我们用空间中的有向线段表示向量.
在本书中三维欧几里得空间中的向量记作
2. 极向量和轴向量
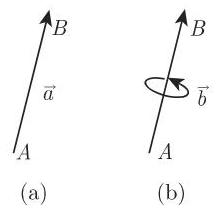
极向量表示具有大小和空间方向的量, 如速度和加速度; 轴向量表示具有大小, 空间方向和旋转方向的量, 如角速度和角加速度. 在图示上它们用极箭头和轴箭头来区别 (图 3.113). 但在数学讨论中对它们并不加以区别.
3. 模和空间中的方向
向量
4. 向量的相等
两个向量
反向的相等向量具有相同的模, 但方向相反:
在这一情形, 轴向量具有相反和相同的旋转方向.
5. 自由向量、固定向量、滑动向量
自由向量被认为是相同的, 即它在做平行移动时不改变模和方向, 因此它的起点可以是空间中的任意一点. 如果一个向量的性质与一个确定的起点相关联, 则它被称为约束向量或固定向量. 滑动向量只能沿它所在的直线移动.
6. 特殊向量
a)单位向量
单位向量
而且还有
成立, 即它是一个规范正交坐标系.
b) 零向量
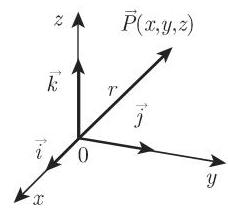
c) 向径
d) 共线向量 是与同一直线平行的向量.
e) 共面向量 是平行于同一平面的向量. 它们满足等式 (3.260).
3.5.1.2 向量的计算法则
1. 向量的和
a) 两个向量
b) 若干个向量
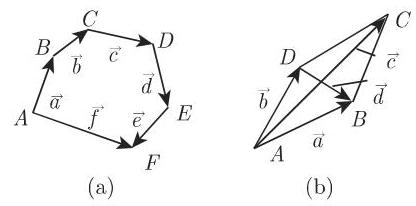
若干个向量之和的重要性质是加法的交换律和结合律. 对于三个向量成立有
c) 两个向量的差
它是平行四边形 (图 3.115(b)) 的另一条对角线. 两个向量之差的最重要性质是
2. 向量与标量的乘法, 线性组合
乘积
(3.238a)
向量
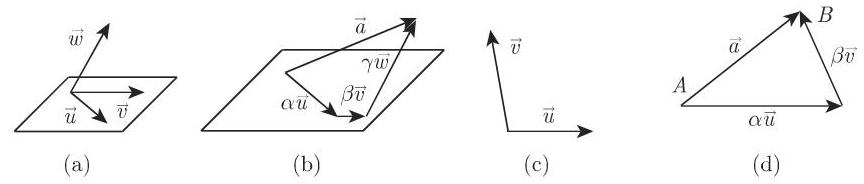
3. 向量的分解
在三维空间中每个向量
这里
3.5.1.3 向量的坐标
1. 笛卡儿坐标
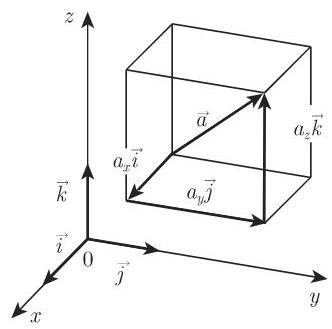
根据 (3.239a),每个向量
其中标量
由单位向量定义的三个方向构成一个正交方向三元组. 向量的分量是该向量在坐标轴上的投影 (图 3.117).
若干个向量的线性组合的坐标等同于这些向量的坐标的线性组合, 因此向量方程(3.238b)对应于下面的坐标方程:
对于两个向量的和与差
的坐标, 有等式
成立. 点
2. 仿射坐标
仿射是笛卡儿坐标的一般化, 它基于三个线性无关但不必正交的向量, 即不共面的基向量
或
当标量
3.5.1.4 方向系数
向量
其中
方向系数代表
在笛卡儿坐标系中,向量
3.5.1.5 标量积与向量积
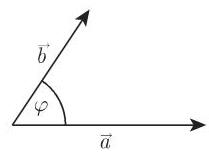
1. 标量积
两个向量
其中
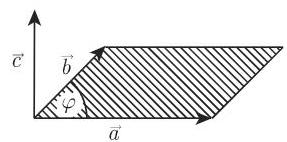
2. 向量积
两个向量
其中
3. 向量的乘积的性质
a) 标量积是可交换的:
b) 向量积是反交换的 (交换因子后改变符号):
c) 与一个标量相乘满足结合律:
d) 结合律对于二重标量积和二重向量积不成立:
e) 分配律成立:
f) 两个向量的正交性 如果等式
成立,并且
g) 两个向量的共线性 如果等式
成立,并且
h) 相同向量的乘法
i)向量的线性组合 可以用和标量多项式相同的方法相乘 (因为分配律成立), 对于向量积来说, 只有一点必须加以注意. 如果交换因子则也要改变符号.
j) 标量不变量是在坐标系的平移和旋转下其值不发生改变的标量. 两个向量的标量积是一个标量不变量.
3.5.1.6 向量乘积的组合
1. 二重向量积
二重向量积
2. 混合积
混合积
交换任何两项的结果将变号; 将全部三项轮换不影响结果.
对于共面向量,即如果
3. 多重乘积的公式
a) 拉格朗日恒等式
4. 用笛卡儿坐标表示的乘积公式
如果将向量
则可以用下面的公式计算乘积:
(1) 标量积
(2) 向量积
(3) 混合积
5. 用仿射坐标表示的乘积公式
(1) 度量系数与互反向量组 如果在
而需要计算标量积
或向量积
(3.269a)
后者用到等式
那么就必须要知道坐标向量的两两乘积. 对于标量积而言这些是六个度量系数:
而对向量积来说是三个向量
它们是关于
是坐标向量混合积的倒数. 这个记号在下面的讨论中仅用来作简写. 借助关于基向量的乘法表 3.13 和表 3.14 容易算出这些系数.
乘数 | ||||
0 | ||||
被乘数 | 0 | |||
0 | ||||
(2) 对于笛卡儿坐标的应用 笛卡儿坐标是仿射坐标的特殊情形. 由表 3.15 和表 3.16 对于基向量
得度量系数
和互反基向量
因此, 该坐标系的基向量与互反向量一致, 换句话说, 在笛卡儿坐标系中基向量组就是它自己的互反组.
1 | 0 | 0 | |
0 | 1 | 0 | |
0 | 0 | 1 |
0 | |||
0 | |||
0 |
(3) 由坐标给出的向量的标量积
对于笛卡儿坐标, (3.273) 与 (3.264) 相符.
在 (3.273) 中的第二个等号后, 用到了一种常在张量计算中表示求和的简记法 (参见第 376 页, 4.3.1, 2.): 只写出通项以取代完整求和, 因此应该对指标重复进行求和计算, 即对每次出现的上下标进行求和计算. 有时用希腊字母表示求和指标; 这里它们的值从 1 取到 3 . 因此有
(4) 由坐标给出的向量的向量积 根据 (3.269a) 有
对于笛卡儿坐标, (3.275) 与 (3.265) 相符.
(5) 由坐标给出的向量的混合积 根据 (3.269a) 有
对于笛卡儿坐标, (3.276) 与 (3.266) 相符.
3.5.1.7 向量方程
表 3.17 概括了最简单的向量方程. 表中
方程 | 解 |
(1) | |
(2) | |
(3) | 这是一个不定方程; 考虑具有相同起点, 满足这一方程的所 有向量 |
(4) | 这是一个不定方程; 考虑具有相同起点, 满足这一方程的所 有向量 |
续表
方程 | 解 |
(5) | |
其中 | |
(7) | |
(8) |
注:
3.5.1.8 向量的共变坐标和反变坐标
1. 定义
向量
定义的仿射坐标
在笛卡儿坐标系中, 向量的共变坐标和反变坐标是一致的.
2. 利用标量积表示坐标
向量
向量
在笛卡儿坐标系中 (3.279) 与 (3.280) 是一致的:
3. 借助坐标表示标量积
用两个向量的反变坐标确定它们的标量积得到公式 (3.273). 对于共变坐标, 相应的公式为
其中
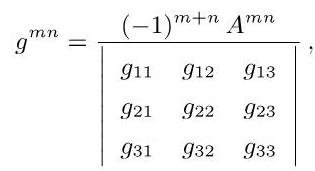
其中
如果向量
类似地, 有
3.5.1.9 向量代数的几何应用
确定向量公式 | 用笛卡儿坐标表示的公式 |
向量 | |
由向量 | |
平行四边形的面积 由向量 | |
平行六面体的体积 | |
向量 |