3.6.1 平面曲线

3.6.1.1 定义平面曲线的方法

1. 坐标方程

(1) 笛卡儿坐标

a) 隐式

$$\begin{array}{}\text{(3.483)}& F\left(x,y\right)=0\end{array}$$

b) 显式

$$\begin{array}{}\text{(3.484)}& y=f\left(x\right),\end{array}$$

(2)参数形式

$$\begin{array}{}\text{(3.485)}& x=x\left(t\right),y=y\left(t\right).\end{array}$$

(3) 极坐标

$$\begin{array}{}\text{(3.486)}& \rho =f\left(\phi \right).\end{array}$$

2. 曲线上的正方向

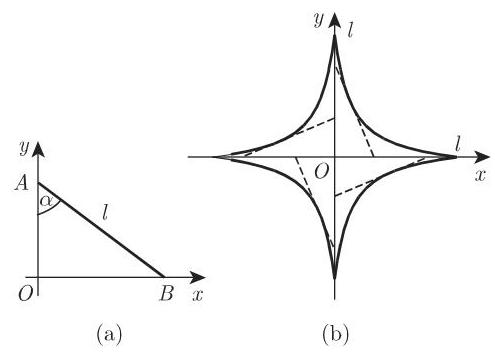
如果曲线是以 (3.485) 的形式给出,则它上面的正方向定义为参数 $t$ 的值增加时曲线上的点 $P\left(x\left(t\right),y\left(t\right)\right)$ 移动的方向. 如果曲线由 (3.484) 的形式给出,则横坐标可以看作参数 $\left(x=x,y=f\left(x\right)\right)$ ,因此正方向相应于横坐标的增加. 对于 (3.486) 的形式可以将角 $\phi$ 看成参数 $\left(x=f\left(\phi \right)\cos \phi ,y=f\left(\phi \right)\sin \phi \right)$ ,因此正方向相应于 $\phi$ 的增加, 即逆时针.

$◼$ 图 3.219(a),(b),(c): $\mathbf{A}$: $x=t^2,y=t^3$ , $\mathbf{B}$: $y=\sin x$ , $\mathbf{C}$: $\rho =a\phi$ .

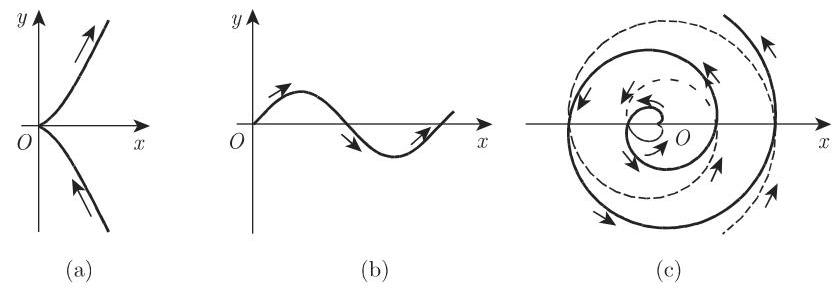
3.6.1.2 曲线的局部元素

依赖于曲线上的动点 $P$ 是否按形式 (3.484) $\sim \left(3.486\right)$ 给出,其位置由 $x,t$ 或 $\phi$ 定义. 在这里以参数值 $x+\mathrm{d}x,t+\mathrm{d}t$ 或 $\phi +\mathrm{d}\phi$ 任意接近于 $P$ 的一个点记作 $N$ .

1. 弧微分

如果 $s$ 表示曲线从一个固定点 $A$ 到点 $P$ 的长,则无穷小增量 $\mathrm{\Delta }s=\stackrel{⏜}{PN}$ 可以近似地由弧长的微分,即弧微分 $\mathrm{d}s$ 表示:

$$\begin{array}{}\text{(3.487)}& \mathrm{\Delta }s\approx \mathrm{d}s=\{\begin{array}{ll}\sqrt{1+{\left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)}^2}\mathrm{d}x,& \text{ 对于形式 (3.484),}\\ \sqrt{x^{\prime 2}+y^{\prime 2}}\mathrm{d}t,& \text{ 对于形式 (3.485),}\\ \sqrt{{\rho }^2+{\rho }^{\prime 2}}\mathrm{d}\phi ,& \text{ 对于形式 (3.486). }\end{array}\end{array}$$

(3.488)

(3.489)

$◼\mathbf{A}$: $y=\sin x,\mathrm{d}s=\sqrt{1+{\cos }^{2}x}\mathrm{d}x$ .

$◼\mathbf{B}$: $x=t^2,y=t^3,\mathrm{d}s=\left|t\right|\sqrt{4+9t^2}\mathrm{d}t$ .

$◼\mathbf{C}$: $\rho =a\phi \left(a>0\right),\mathrm{d}s=a\sqrt{1+{\phi }^2}\mathrm{d}\phi$ .

2. 切线和法线

(1) 曲线在点 $P$ 处的切线 是割线 $PN$ 当 $N\to P$ 时处于极限位置的一条直线; 此处的法线是过 $P$ 垂直于切线的一条直线 (图 3.220).

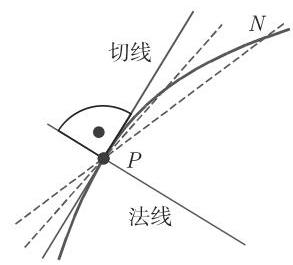
(2) 切线和法线的方程 针对 (3.483), (3.484) 和 (3.485) 三种情形在表 3.26 中给出. 这里 $x,y$ 是 $P$ 的坐标, $X,Y$ 是切线和法线上点的坐标. 导数值应在 $P$ 点处计算.

方程类型	切线方程	法线方程
(3.483)	$\frac{\partial F}{\partial x}\left(X-x\right)+\frac{\partial F}{\partial y}\left(Y-y\right)=0$	$\frac{X-x}{\frac{\partial F}{\partial x}}=\frac{Y-y}{\frac{\partial F}{\partial y}}$
(3.484)	$Y-y=\frac{\mathrm{d}y}{\mathrm{d}x}\left(X-x\right)$	$Y-y=-\frac{1}{\frac{\mathrm{d}y}{\mathrm{d}x}}$
(3.485)	$\frac{Y-y}{y^{\prime }}=\frac{X-x}{x^{\prime }}$	$x^{\prime }\left(X-x\right)+y^{\prime }\left(Y-y\right)=0$

关于曲线的切线方程和法线方程的一些例子

$◼\mathbf{A}$: 圆 $x^2+y^2=25$ 在点 $P\left(3,4\right)$ :

a) 切线方程 $2x\left(X-x\right)+2y\left(Y-y\right)=0$ 或 $Xx+Yy=25$ ,考虑到点 $P$ 位于圆上,有: $3X+4Y=25$ .

b) 法线方程 $\frac{X-x}{2x}=\frac{Y-y}{2y}$ 或 $Y=\frac{y}{x}X$ ; 在点 $P:Y=\frac{4}{3}X$ .

$◼\mathbf{B}$: 正弦曲线 $y=\sin x$ 在点 $O\left(0,0\right)$ :

a) 切线方程 $Y-\sin x=\cos x\left(X-x\right)$ 或 $Y=X\cos x+\sin x-x\cos x$ ; 在点 $\left(0,0\right):Y=X$ .

b) 法线方程 $Y-\sin x=-\frac{1}{\cos x}\left(X-x\right)$ 或 $Y=-X\sec x+\sin x+x\sec x$ ; 在点 $\left(0,0\right):Y=-X$ .

$◼\mathbf{C}$: 曲线 $x=t^2,y=t^3$ 在点 $P\left(4,-8\right),t=-2$ :

a) 切线方程 $\frac{Y-t^3}{3t^2}=\frac{X-t^2}{2t}$ 或 $Y=\frac{3}{2}tX-\frac{1}{2}{t}^3$ ; 在点 $P:Y=-3X+4$ .

b) 法线方程: $2t\left(X-t^2\right)+3t^2\left(Y-t^3\right)=0$ 或 $2X+3tY=t^2\left(2+3t^2\right)$ ; 在点 $P\left(4,-8\right):X-3Y=28$ .

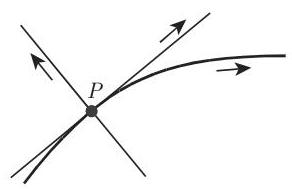
(3) 曲线的切线和法线的正方向 如果曲线由 (3.484), (3.485), (3.486) 中的形式之一给出, 则切线和法线上的正方向按以下方式定义: 切线的正方向与切点处曲线的正方向相同,而从切线的正方向逆时针围绕 $P$ 旋转 ${90}^{\circ }$ 则得到法线的正方向 (图 3.221). 切线和法线被点 $P$ 分成正的和负的半直线.

(4)切线的斜率 可以由以下度量确定:

a) 切线的斜率角 $\alpha$ ,即横坐标轴的正向与切线的夹角,或

b) 角 $\mu$ (如果曲线由极坐标给出),即向径 $OP\left(\overline{OP}=\rho \right)$ 与切线正方向之间的夹角 (图 3.222). 对于角 $\alpha$ 和 $\mu$ 下列公式成立,其中 $\mathrm{d}s$ 按 (3.487) 至 (3.489) 计算:

$$\begin{array}{}\text{(3.490a)}& \tan \alpha =\frac{\mathrm{d}y}{\mathrm{d}x},\cos \alpha =\frac{\mathrm{d}x}{\mathrm{d}s},\sin \alpha =\frac{\mathrm{d}y}{\mathrm{d}s};\end{array}$$$$\begin{array}{}\text{(3.490b)}& \tan \mu =\frac{\rho }{\frac{\mathrm{d}\rho }{\mathrm{d}\phi }},\cos \mu =\frac{\mathrm{d}\rho }{\mathrm{d}s},\sin \mu =\rho \frac{\mathrm{d}\phi }{\mathrm{d}s}.\end{array}$$

$◼\mathbf{A}$: $y=\sin x,\tan \alpha =\cos x,\cos \alpha =\frac{1}{\sqrt{1+{\cos }^{2}x}},\sin \alpha =\frac{\cos x}{\sqrt{1+{\cos }^{2}x}}\text{; }$

$◼\mathbf{B}$: $x=t^2,y=t^3,\tan \alpha =\frac{3t}{2},\cos \alpha =\frac{2}{\sqrt{4+9t^2}},\sin \alpha =\frac{3t}{\sqrt{4+9t^2}}\text{;}$

$◼\mathbf{C}$: $\rho =a\phi ,\tan \mu =\phi ,\cos \mu =\frac{1}{\sqrt{1+{\phi }^2}},\sin \mu =\frac{\phi }{\sqrt{1+{\phi }^2}}$ .

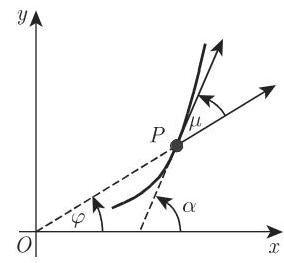
(5)切线和法线线段, 次切距和次法距(图 3.223)

a) 应用笛卡儿坐标对于 (3.484), (3.485) 形式的定义有

$$\begin{array}{}\text{(3.491a)}& \overline{PT}=\left|\frac{y}{y^{\prime }}\sqrt{1+{y^{\prime }}^2}\right|\text{ (切线线段),}\end{array}$$$$\begin{array}{}\text{(3.491b)}& \overline{PN}=\left|y\sqrt{1+y^{\prime 2}}\right|\text{ (法线线段),}\end{array}$$$$\begin{array}{}\text{(3.491c)}& \overline{P^{\prime }T}=\left|\frac{y}{y^{\prime }}\right|\text{ (次切距),}\end{array}$$$$\begin{array}{}\text{(3.491d)}& \overline{P^{\prime }N}=\left|y{y}^{\prime }\right|\text{ (次法距). }\end{array}$$

b) 应用极坐标对于 (3.486) 形式的定义有

$$\begin{array}{}\text{(3.492a)}& \overline{P{T}^{\prime }}=\left|\frac{\rho }{{\rho }^{\prime }}\sqrt{{\rho }^2+{\rho }^{\prime 2}}\right|\text{ (极切线线段),}\end{array}$$$$\begin{array}{}\text{(3.492b)}& \overline{P{N}^{\prime }}=\left|\sqrt{{\rho }^2+{\rho }^{\prime 2}}\right|\text{ (极法线线段),}\end{array}$$$$\begin{array}{}\text{(3.492c)}& \overline{O{T}^{\prime }}=\left|\frac{{\rho }^2}{{\rho }^{\prime }}\right|\text{ (极次切距),}\end{array}$$$$\begin{array}{}\text{(3.492d)}& \overline{O{N}^{\prime }}=\left|{\rho }^{\prime }\right|\text{ (极次法距). }\end{array}$$

$◼\mathbf{A}$: $y=\cosh x,y^{\prime }=\sinh x,\sqrt{1+y^{\prime 2}}=\cosh x;\overline{PT}=\left|\cosh x\coth x\right|,\overline{PN}=$$\left|{\cosh }^{2}x\right|,\overline{P^{\prime }T}=\left|\coth x\right|,\overline{P^{\prime }N}=\left|\sinh x\cosh x\right|.$

$◼\mathbf{B}$: $\rho =a\phi \left(a>0\right),{\rho }^{\prime }=a,\sqrt{{\rho }^2+{\rho }^{\prime 2}}=a\sqrt{1+{\phi }^2};\overline{P{T}^{\prime }}=\left|a\phi \sqrt{1+{\phi }^2}\right|$ ,$\overline{P{N}^{\prime }}=\left|a\sqrt{1+{\phi }^2}\right|,\overline{O{T}^{\prime }}=\left|a{\phi }^2\right|,\overline{O{N}^{\prime }}=a.$

(6) 两曲线之间的夹角 两曲线 ${\mathrm{\Gamma }}_1$ 和 ${\mathrm{\Gamma }}_2$ 在它们的交点 $P$ 处的夹角 $\beta$ 定义为它们的切线在点 $P$ 处的夹角 (图 3.224). 根据这一定义,角 $\beta$ 的计算简化为斜率是

$$\begin{array}{}\text{(3.493a)}& k_1=\tan {\alpha }_1={\left(\frac{\mathrm{d}{f}_1}{\mathrm{d}x}\right)}_P,\end{array}$$$$\begin{array}{}\text{(3.493b)}& k_2=\tan {\alpha }_2={\left(\frac{\mathrm{d}{f}_2}{\mathrm{d}x}\right)}_P\end{array}$$

的两条直线之间夹角的计算. 这里 $y=f_1\left(x\right)$ 是 ${\mathrm{\Gamma }}_1$ 的方程而 $y=f_2\left(x\right)$ 是 ${\mathrm{\Gamma }}_2$ 的方程,导数是在 $P$ 点处计算的. 借助公式

$$\begin{array}{}\text{(3.494)}& \tan \beta =\tan \left({\alpha }_2-{\alpha }_1\right)=\frac{\tan {\alpha }_2-\tan {\alpha }_1}{1+\tan {\alpha }_1\tan {\alpha }_2}\end{array}$$

我们得到 $\beta$ .

$◼$ 确定抛物线 $y=\sqrt{x}$ 和 $y=x^2$ 在点 $P\left(1,1\right)$ 处的夹角:

$$\tan {\alpha }_1={\left(\frac{\mathrm{d}\sqrt{x}}{\mathrm{d}x}\right)}_{x=1}=\frac{1}{2},\tan {\alpha }_2={\left(\frac{\mathrm{d}\left(x^2\right)}{\mathrm{d}x}\right)}_{x=1}=2,$$$$\tan \beta =\frac{\tan {\alpha }_2-\tan {\alpha }_1}{1+\tan {\alpha }_1\tan {\alpha }_2}=\frac{3}{4}.$$

3. 曲线的凸和凹部分

如果一条曲线由显式函数 $y=f\left(x\right)$ 给出,则可以检查在包含点 $P$ 的一小部分曲线是上凹还是下凹,当然 $P$ 是拐点或奇点除外 (参见第 334 页 3.6.1.3). 如果二阶导数 $f^{\prime \prime }\left(x\right)>0$ (假如存在的话),则曲线是上凹的,即朝 $y$ 的正向 (图 3.225 中的点 $P_2$ ). 如果 $f^{\prime \prime }\left(x\right)<0$ 成立 (点 $P_1$ ),则曲线是下凹的. 在 $f^{\prime \prime }\left(x\right)=0$ 的情形应该检验它是否是拐点. $◼y=x^3$ (图 2.15(b)); $y^{\prime \prime }=6x$ ,对于 $x>0$ 曲线是上凹的,对于 $x<0$ 曲线是下凹的.

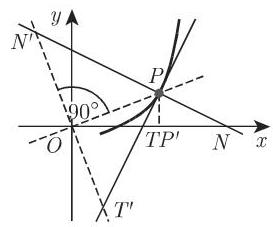
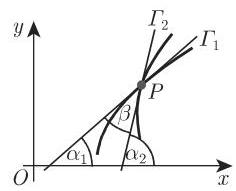
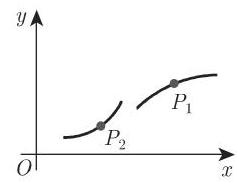
图 3.223 图 3.224

4. 曲率和曲率半径

(1) 曲线的曲率 曲线在点 $P$ 处的曲率 $K$ 是点 $P$ 和 $N$ 处的正切线方向之间的夹角 $\delta$ (图 3.226) 与弧长 $\stackrel{⏜}{PN}$ (当 $\stackrel{⏜}{PN}\to 0$ 时) 之比的极限:

$$\begin{array}{}\text{(3.495)}& K=\underset{\stackrel{⏜}{PN}\to 0}{lim}\frac{\delta }{\stackrel{⏜}{PN}}\end{array}$$

曲率 $K$ 的符号依赖于该曲线朝法线正的一半 $\left(K>0\right)$ 弯曲还是朝法线负的一半 $\left(K<0\right)$ 弯曲 (参见第 327 页 3.6.1.1,2.). 换句话说,曲率中心对于 $K>0$ 而言是在法线的正侧,对于 $K<0$ 而言是在法线的负侧. 有时曲率 $K$ 仅被看成是一个正的量. 于是上述极限取绝对值.

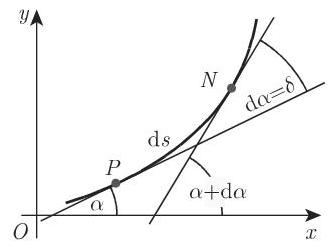
(2) 曲线的曲率半径 曲线在点 $P$ 处的曲率半径 $R$ 是曲率绝对值的倒数:

$$\begin{array}{}\text{(3.496)}& R=\frac{1}{\left|K\right|}.\end{array}$$

在点 $P$ 处的曲率越大,曲率半径越小.

$◼\mathbf{A}$: 对于半径为 $a$ 的圆,每点处的曲率 $K=\frac{1}{a}$ 而曲率半径 $R=a$ 是常数.

$◼\mathbf{B}$: 对于直线有 $K=0,R=\mathrm{\infty }$ .

(3)曲率和曲率半径的公式

使用通常的记号 $\delta =\mathrm{d}\alpha$ 和 $\stackrel{⏜}{PN}=\mathrm{d}s$ ,有

$$\begin{array}{}\text{(3.497)}& K=\frac{\mathrm{d}\alpha }{\mathrm{d}s},R=\left|\frac{\mathrm{d}s}{\mathrm{d}\alpha }\right|.\end{array}$$

对于第 326 页 3.6.1.1 曲线的不同定义公式, $K$ 和 $R$ 的不同表达式为:

按 (3.484) 中的定义:

$$\begin{array}{}\text{(3.498)}& K=\frac{\frac{{\mathrm{d}}^{2}y}{\mathrm{d}{x}^2}}{{[1+{\left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)}^2]}^{3/2}},R=\left|\frac{{[1+{\left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)}^2]}^{3/2}}{\frac{{\mathrm{d}}^{2}y}{\mathrm{d}{x}^2}}\right|.\end{array}$$

按 (3.485) 中的定义:

$$\begin{array}{}\text{(3.499)}& K=\frac{\left|\begin{array}{cc}{x}^{\prime }& y^{\prime }\\ x^{\prime \prime }& y^{\prime \prime }\end{array}\right|}{{(x^{\prime 2}+y^{\prime 2})}^{3/2}},R=\left|\frac{{(x^{\prime 2}+y^{\prime 2})}^{3/2}}{\left|\begin{array}{cc}{x}^{\prime }& y^{\prime }\\ x^{\prime \prime }& y^{\prime \prime }\end{array}\right|}\right|.\end{array}$$

按 (3.483) 中的定义:

$$\begin{array}{}\text{(3.500)}& K=\frac{\left|\begin{array}{ccc}{F}_{xx}& F_{xy}& F_x\\ F_{yx}& F_{yy}& F_y\\ F_x& F_y& 0\end{array}\right|}{{(F_x^2+F_y^2)}^{3/2}},R=\left|\frac{{(F_x^2+F_y^2)}^{3/2}}{\left|\begin{array}{ccc}{F}_{xx}& F_{xy}& F_x\\ F_{yx}& F_{yy}& F_y\\ F_{yx}& F_{yy}& F_y\\ F_{xy}& 0& \end{array}\right|}\right|.\end{array}$$

按 (3.486) 中的定义:

$$\begin{array}{}\text{(3.501)}& K=\frac{{\rho }^2+2{\rho }^{\prime 2}-\rho {\rho }^{\prime \prime }}{{({\rho }^2+{\rho }^{\prime 2})}^{3/2}},R=\left|\frac{{({\rho }^2+{\rho }^{\prime 2})}^{3/2}}{{\rho }^2+2{\rho }^{\prime 2}-\rho {\rho }^{\prime \prime }}\right|.\end{array}$$

$◼\mathbf{A}$: $y=\cosh x,K=\frac{1}{{\cosh }^{2}x};$

$◼\mathbf{B}$: $x=t^2,y=t^3,K=\frac{6}{t{(4+9t^2)}^{3/2}};$

$◼\mathbf{C}$: $y^2-x^2=a^2,K=\frac{a^2}{{(x^2+y^2)}^{3/2}}\text{;}$

$◼\mathbf{D}$: $\rho =a\phi ,K=\frac{1}{a}\cdot \frac{{\phi }^2+2}{{({\phi }^2+1)}^{3/2}}$ .

5. 曲率圆和曲率中心

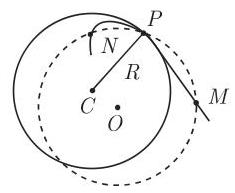
(1) 曲率圆 在 $P$ 点处的曲率圆是过 $P$ 和曲线上两个邻近的点 $N$ 和 $M$ 的圆当 $N\to P$ 和 $M\to P$ 时的极限位置 (图 3.227). 它过曲线上的点并在此具有与曲线相同的一阶导数和二阶导数. 因此它在切点处对曲线拟合得特别好. 曲率圆也称为密切圆. 它的半径是曲率半径, 其值是曲率绝对值的倒数.

(2) 曲率中心 曲率圆的中心 $C$ 是点 $P$ 的曲率中心. 它位于曲线凹的一侧,并在该曲线的法线上.

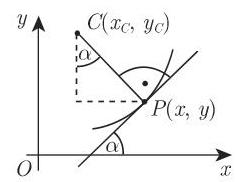
(3) 曲率中心的坐标 对于由第 326 页 3.6.1.1 中的方程定义的曲线, 其曲率中心的坐标 $\left(x_C,y_C\right)$ 可以用以下公式确定.

按 (3.484) 中的定义:

$$\begin{array}{}\text{(3.502)}& x_C=x-\frac{\frac{\mathrm{d}y}{\mathrm{d}x}\left[1+{\left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)}^2\right]}{\frac{{\mathrm{d}}^{2}y}{\mathrm{d}{x}^2}},y_C=y+\frac{1+{\left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)}^2}{\frac{{\mathrm{d}}^{2}y}{\mathrm{d}{x}^2}}.\end{array}$$

按 (3.485) 中的定义:

$$\begin{array}{}\text{(3.503)}& x_C=x-\frac{y^{\prime }\left(x^{\prime 2}+y^{\prime 2}\right)}{\left|\begin{array}{cc}{x}^{\prime }& y^{\prime }\\ x^{\prime \prime }& y^{\prime \prime }\end{array}\right|},y_C=y+\frac{x^{\prime }\left(x^{\prime 2}+y^{\prime 2}\right)}{\left|\begin{array}{cc}{x}^{\prime }& y^{\prime }\\ x^{\prime \prime }& y^{\prime \prime }\end{array}\right|}.\end{array}$$

按 (3.486) 中的定义:

$$x_C=\rho \cos \phi -\frac{\left({\rho }^2+{\rho }^{\prime 2}\right)\left(\rho \cos \phi +{\rho }^{\prime }\sin \phi \right)}{{\rho }^2+2{\rho }^{\prime 2}-\rho {\rho }^{\prime \prime }},$$$$\begin{array}{}\text{(3.504)}& y_C=\rho \sin \phi -\frac{\left({\rho }^2+{\rho }^{\prime 2}\right)\left(\rho \sin \phi -{\rho }^{\prime }\cos \phi \right)}{{\rho }^2+2{\rho }^{\prime 2}-\rho {\rho }^{\prime \prime }}.\end{array}$$

按 (3.483) 中的定义:

$$\begin{array}{}\text{(3.505)}& \begin{array}{l}{x}_C=x+\frac{F_x\left(F_x^2+F_y^2\right)}{\left|\begin{array}{lll}{F}_{xx}& F_{xy}& F_x\\ F_{yx}& F_{yy}& F_y\\ F_{yx}& F_{yy}& F_y\end{array}\right|},y_C=y+\frac{F_y\left(F_x^2+F_y^2\right)}{\left|\begin{array}{lll}{F}_{xx}& F_{xy}& F_x\\ F_{yx}& F_{yy}& F_y\\ F_x& F_y& 0\end{array}\right|}.\end{array}\end{array}$$

这些公式可以变换成形式

$$\begin{array}{}\text{(3.506)}& x_C=x-R\sin \alpha ,y_C=y+R\cos \alpha \end{array}$$

或

$$\begin{array}{}\text{(3.507)}& x_C=x-R\frac{\mathrm{d}y}{\mathrm{d}s},y_C=y+R\frac{\mathrm{d}x}{\mathrm{d}s}\text{ (图 3.228). }\end{array}$$

其中 $R$ 应该像在 (3.498) 至 (3.501) 中那样计算.

3.6.1.3 曲线的特殊点

以下仅讨论在坐标变换下仍保持不变的点. 极大值和极小值的确定见第 596 页6.1.5.3.

1. 拐点及其确定规则

拐点是曲线上曲率改变其符号的点 (图 3.229). 拐点处的切线与曲线相交, 因此在它附近曲线位于切线的两侧. 在拐点有 $K=0$ 且 $R=\mathrm{\infty }$ .

(1) 曲线的显定义式 $\left(3.484\right)y=f\left(x\right)$ .

a) 必要条件如果曲线上一点处存在二阶导数, 则该点为拐点的必要条件是此二阶导数的值为零 (关于不存在二阶导数的情形见 b))

$$\begin{array}{}\text{(3.508)}& f^{\prime \prime }\left(x\right)=0\end{array}$$

在二阶导数存在的情形,为了确定拐点,需要找出 $f^{\prime \prime }\left(x\right)=0$ 的所有根 $x_1,x_2,\cdots$ , $x_i,\cdots ,x_n$ ,并将它们代入接下来所求的更高阶导数中. 如果对于值 $x_i$ 而言的第一个非零导数具有奇数阶, 则在此存在一个拐点. 如果所考虑的点不是一个拐点, 因为第一个不为零的导数阶数 $k$ 是偶数,则对于 $f^{\left(k\right)}\left(x\right)<0$ 有曲线是下凹的; 对于 $f^{\left(k\right)}\left(x\right)>0$ 有曲线是上凹的. 对于高阶导数无法检验的情形,例如它们不存在时, 见b).

b) 充分条件 拐点存在的一个充分条件是当从该点左侧过渡到右侧时二阶导数 $f^{\prime \prime }\left(x\right)$ 的符号发生改变. 因此曲线在横坐标为 $x_i$ 的点是否具有拐点的问题,可以通过检验经该点的二阶导数的符号来回答: 如果经过时符号发生改变, 则存在一个拐点. 这一方法也可以用于 $y^{\prime \prime }=\mathrm{\infty }$ 的情形.

$◼\mathbf{A}$: $y=\frac{1}{1+x^2},f^{\prime \prime }\left(x\right)=-2\frac{1-3x^2}{{(1+x^2)}^3},x_{1,2}=\pm \frac{1}{\sqrt{3}},f^{\prime \prime \prime }\left(x\right)=24x\frac{1-x^2}{{(1+x^2)}^4}$ , $f^{\prime \prime \prime }\left(x_{1,2}\right)\ne 0$ . 拐点: $A\left(\frac{1}{\sqrt{3}},\frac{3}{4}\right),B\left(-\frac{1}{\sqrt{3}},\frac{3}{4}\right)$ .

$◼\mathbf{B}$: $y=x^4,f^{\prime \prime }\left(x\right)=12x^2,x_1=0,f^{\prime \prime \prime }\left(x\right)=24x,f^{\prime \prime \prime }\left(x_1\right)=0,f^{IV}\left(x\right)=24$ ; 不存在拐点.

$◼\mathbf{C}$: $y=x^{\frac{5}{3}},y^{\prime }=\frac{5}{3}{x}^{\frac{2}{3}},y^{\prime \prime }=\frac{10}{9}{x}^{-\frac{1}{3}}$ ; 对 $x=0$ 我们有 $y^{\prime \prime }=\mathrm{\infty }$ .

由于 $x$ 的值在从负到正的变化过程中,二阶导数的符号从 “-” 变到 “+”,因此曲线在 $x=0$ 处具有拐点.

评论 在实践中, 如果从曲线的形状推出拐点存在, 例如在具有连续导数的极大值和极小值之间,则仅确定点 $x_i$ 而不检验更高阶的导数.

(2) 曲线的其他定义形式 针对 (3.484) 情形的曲线定义形式而得到的拐点存在的必要条件 (3.508) 对于其他的定义公式将具有如下的分析形式: a) 按 (3.485) 中的参数形式定义:

$$\begin{array}{}\text{(3.509)}& \left|\begin{array}{cc}{x}^{\prime }& y^{\prime }\\ x^{\prime \prime }& y^{\prime \prime }\end{array}\right|=0\end{array}$$

b) 按 (3.486) 中的极坐标定义:

$$\begin{array}{}\text{(3.510)}& {\rho }^2+2{\rho }^{\prime 2}-\rho {\rho }^{\prime \prime }=0.\end{array}$$

c) 按 (3.483) 中的隐式定义:

$$\begin{array}{}\text{(3.511)}& F\left(x,y\right)=0\text{ 和 }\left|\begin{array}{ccc}{F}_{xx}& F_{xy}& F_x\\ F_{yx}& F_{yy}& F_y\\ F_x& F_y& 0\end{array}\right|=0.\end{array}$$

在这些情形中, 解系给出了可能拐点的坐标.

$◼\mathbf{A}$: $x=a\left(t-\frac{1}{2}\sin t\right),y=a\left(1-\frac{1}{2}\cos t\right)$ (参见第 132 页短摆线 (图 2.68b));

$$\left|\begin{array}{cc}{x}^{\prime }& y^{\prime }\\ x^{\prime \prime }& y^{\prime \prime }\end{array}\right|=\frac{a^2}{4}\left|\begin{array}{cc}2-\cos t& \sin t\\ \sin t& \cos t\end{array}\right|=\frac{a^2}{4}\left(2\cos t-1\right);$$$$\cos t_k=\frac{1}{2};t_k=\pm \frac{\pi }{3}+2k\pi \left(k=0,\pm 1,\pm 2,\cdots \right).$$

对于参数值 $t_k$ 该曲线具有无穷多个拐点.

$◼\mathbf{B}$: $\rho =\frac{1}{\sqrt{\phi }};{\rho }^2+2{\rho }^{\prime 2}-\rho {\rho }^{\prime \prime }=\frac{1}{\phi }+\frac{1}{2{\phi }^3}-\frac{3}{4{\phi }^3}=\frac{1}{4{\phi }^3}\left(4{\phi }^2-1\right)$ . 拐点位于角

$$\phi =\frac{1}{2}.$$$$\text{【C:}{x}^2-y^2=a^2\text{(双曲线).}\left|\begin{array}{ccc}{F}_{xx}& \cdot & \cdot \\ \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot \end{array}\right|=\left|\begin{array}{ccc}2& 0& 2x\\ 0& -2& -2y\\ 2x& -2y& 0\end{array}\right|=8x^2-8y^2\text{. 方}$$

程 $x^2-y^2=a^2$ 和 $8\left(x^2-y^2\right)=0$ 相互矛盾,因此双曲线没有拐点.

2. 顶点

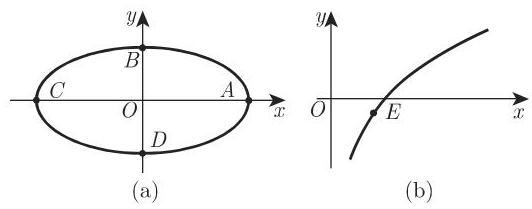
顶点是曲线上曲率具有极大值或极小值的点. 例如椭圆具有四个顶点 $A,B,C$ , $D$ ,对数函数的曲线在 $E\left(\frac{1}{\sqrt{2}},-\frac{\ln 2}{2}\right)$ 处具有一个顶点 (图 3.230). 确定顶点可以转化成确定 $K$ 的极值,或者 $R$ 的极值,如果这样做更简单的话. 公式 (3.498) $\sim \left(3.501\right)$ 可用来计算.

3. 奇点

奇点是曲线上各种特殊点的总称.

(1) 奇点的类型 点a), b), $\cdots ,\mathrm{j})$ 对应于图 3.231 中的表示.

a) 二重点 在二重点曲线与自己相交 (图 3.231(a)).

b) 孤立点 孤立点满足曲线的方程; 但它与该曲线分离 (图 3.231(b)).

c), d) 尖点 在尖点处曲线的方向发生改变; 根据切线的位置可以区分出第一类尖点和第二类尖点 (图 3.231(c), (d)).

e) 密切点 在密切点处曲线与自身接触 (图 3.231(e)).

f) 角点 在角点处曲线突然改变其方向, 但与尖点不同的是在此曲线的两不同支具有两条不同的切线 (图 3.231(f)).

g) 终点 在终点处曲线终止 (图 3.231(g)).

h) 渐近点 在渐近点附近当曲线任意趋近于它时通常将环绕无限次.

i), j) 更多的奇点 有可能曲线在同一点处具有两个或更多的这样的奇点 (图 3.231(i), (j)).

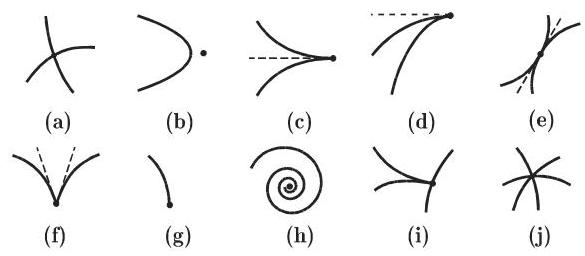
(2) 密切点、角点、终点和渐近点的确定 这些类型的奇点仅在超越函数 (参见第 261 页 3.5.2.5) 的曲线上出现.

角点相应于导数 $\frac{\mathrm{d}y}{\mathrm{d}x}$ 的有限跳跃.

曲线的终点相应于函数 $y=f\left(x\right)$ 具有有限跳跃的间断点或直接终止.

渐近点可以在曲线由极坐标形式 $\rho =f\left(\phi \right)$ 给出的情形中以最容易的方式确定. 如果当 $\phi \to \mathrm{\infty }$ 或 $\phi \to -\mathrm{\infty }$ 时,极限等于 0 $\left(lim\rho =0\right)$ ,这极点是一个渐近点.

$◼\mathbf{A}$: 对于曲线 $y=\frac{x}{1+{\mathrm{e}}^{\frac{1}{x}}}$ (图 6.2c)(参见第 582 页 6.1.1) 原点是一个角点.

$◼\mathbf{B}$: 点(1,0)和(1,1)是函数 $y=\frac{1}{1+{\mathrm{e}}^{\frac{1}{x-1}}}$ (图 2.8)(参见第 70 页 2.1.4.5) 的间断点.

$◼\mathbf{C}$: 对数螺线 $\rho =a{\mathrm{e}}^{k\phi }$ (图 2.75)(参见第 138 页 2.14.3) 在原点处具有一个渐近点.

(3) 多重点的确定 (情形 a) 到 e), 以及 i) 和 j)) 这里用一般术语多重点表示二重点、三重点等等. 为了确定它们,我们从形式为 $F\left(x,y\right)=0$ 的曲线方程出发. 满足三个方程 $F=0,F_x=0$ 和 $F_y=0$ 具有坐标 $\left(x_1,y_1\right)$ 的一个点 $A$ ,当三个二阶导数 $F_{xx},F_{xy}$ 和 $F_{yy}$ 至少一个不为零时是一个二重点. 否则 $A$ 是一个三重点或具有更高重数的点.

二重点的性质依赖于雅可比行列式

$$\begin{array}{}\text{(3.512)}& \mathrm{\Delta }={\left|\begin{array}{ll}{F}_{xx}& F_{xy}\\ F_{yx}& F_{yy}\end{array}\right|}_{\left(\begin{array}{l}x=x_1\\ y=y_1\end{array}\right)}\end{array}$$

的符号.

情形 $\mathrm{\Delta }<0$ 当 $\mathrm{\Delta }<0$ 时曲线在点 $A$ 处自身相交; 在点 $A$ 处切线的斜率是方程

$$\begin{array}{}\text{(3.513)}& F_{yy}{k}^2+2F_{xy}k+F_{xx}=0.\end{array}$$

的根.

情形 $\mathrm{\Delta }>0$ 当 $\mathrm{\Delta }>0$ 时 $A$ 是一个孤立点.

情形 $\mathrm{\Delta }=0$ 当 $\mathrm{\Delta }=0$ 时 $A$ 要么是一个尖点要么是一个密切点; 切线的斜率

是

$$\begin{array}{}\text{(3.514)}& \tan \alpha =-\frac{F_{xy}}{F_{yy}}.\end{array}$$

关于多重点的更详细的研究,建议将坐标系原点平移到点 $A$ 并旋转坐标系使得 $x$ 轴成为点 $A$ 处的切线. 则从方程的形式人们可以说出它是第一类还是第二类尖点, 或是一个密切点.

$◼\mathbf{A}$: $F\left(x,y\right)\equiv {(x^2+y^2)}^2-2a^2\left(x^2-y^2\right)=0$ (参见第 131 页 2.12.6,图 2.66,双纽线); $F_x=4x\left(x^2+y^2-a^2\right),F_y=4y\left(x^2+y^2+a^2\right)$ ; 方程组 $F_x=0,F_y=0$ 导致三个解 $\left(0,0\right),\left(\pm a,0\right)$ ,其中只有一个满足条件 $F=0$ . 将(0,0)代入二阶导数得 $F_{xx}=-4a^2,F_{xy}=0,F_{yy}=+4a^2;\mathrm{\Delta }=-16a^4<0$ ,即在原点处曲线自身相交; 切线的斜率是 $\tan \alpha =\pm 1$ ,其方程为 $y=\pm x$ .

$◼\mathbf{B}$: $F\left(x,y\right)\equiv x^3+y^3-x^2-y^2=0;F_x=x\left(3x-2\right),F_y=y\left(3y-2\right)$ ; 点 $(0$ , $0),\left(0,2/3\right),\left(2/3,0\right)$ 和 $\left(\frac{2}{3},\frac{2}{3}\right)$ 中只有第一个在曲线上; 有 $F_{xx}=-2,F_{xy}=0$ , $F_{yy}=-2,\mathrm{\Delta }=4>0$ ,即原点是一个孤立点.

$◼\mathbf{C}$: $F\left(x,y\right)\equiv {(y-x^2)}^2-x^5=0$ . 方程组 $F_x=0,F_y=0$ 仅得到一个解(0,0), 它也满足方程 $F=0$ . 而且有 $\mathrm{\Delta }=0$ 和 $\tan \alpha =0$ ,因此原点是一个第二类尖点. 这可以从方程的显式形式 $y=x^2\left(1\pm \sqrt{x}\right)$ 看出. 对于 $x<0,y$ 没有定义,而对于 $0<x<1,y$ 的两个值都是正的; 在原点处切线是水平的.

(4) $F\left(x,y\right)=0(F\left(x,y\right)$ 是关于 $x$ 和 $y$ 的多项式) 类型的代数曲线

如果方程不包含常数和一次项, 则原点是一个二重点. 对应的切线可以通过使二次项之和相等来确定.

$◼$ 对于双纽线 (参见第 131 页图 2.66) 在原点处的切线方程 $y=\pm x$ 可以由 $x^2-y^2$ $=0$ 推出.

如果方程也不包含二次项但包含三次项, 则原点是一个三重点.

3.6.1.4 曲线的渐近线

1. 定义

渐近线是当曲线远离原点时无限趋近的一条直线 (图 3.232).

曲线可以从一侧趋近于该直线 (图 3.232(a)), 或在趋近的过程中与它不断相交 (图 3.232(b)).

并不是任何一条曲线在无限地远离原点时 (曲线的无穷分支) 都有一条渐近线. 例如, 作为一种渐近逼近的假分式的整式部分 (参见第 18 页 1.1.7.2).

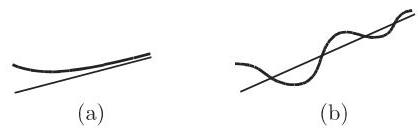
2. 以参数形式 $x=x\left(t\right),y=y\left(t\right)$ 给出的函数

为了确定渐近线的方程,首先确定 $t\to t_i$ 时得出 $x\left(t\right)\to \pm \mathrm{\infty }$ 或 $y\left(t\right)\to \pm \mathrm{\infty }$ (或两者) 的那些值.

有下列情形:

a) 对于 $t\to t_i$ 有 $x\left(t\right)\to \mathrm{\infty }$ 但 $y\left(t_i\right)=a\ne \mathrm{\infty }:y=a$ . 渐近线是水平直线.

(3.515a)

b) 对于 $t\to t_i$ 有 $y\left(t\right)\to \mathrm{\infty }$ 但 $x\left(t_i\right)=a\ne \mathrm{\infty }:x=a$ . 渐近线是垂直直线.(3.515b)

c) 如果 $y\left(t\right)$ 和 $x\left(t\right)$ 两者都趋向 $\pm \mathrm{\infty }$ ,则要计算下列极限:

$$k=\underset{t\to t_i}{lim}\frac{y\left(t\right)}{x\left(t\right)}\text{ 和 }b=\underset{t\to t_i}{lim}\left[y\left(t\right)-kx\left(t\right)\right].$$

如果两者都存在, 则渐近线方程为

$$\begin{array}{}\text{(3.515c)}& y=kx+b.\end{array}$$

If $x=\frac{m}{\cos t},y=n\left(\tan t-t\right),t_1=\frac{\pi }{2},t_2=-\frac{\pi }{2}$ ,确定在 $t_i$ 点的渐近线:

$$x\left(t_1\right)=y\left(t_1\right)=\mathrm{\infty },k=\underset{t\to \pi /2}{lim}\frac{n}{m}\left(\sin t-t\cos t\right)=\frac{n}{m},$$$$b=\underset{t\to \pi /2}{lim}\left[n\left(\tan t-t\right)-\frac{n}{m}\frac{m}{\cos t}\right]=n\underset{t\to \pi /2}{lim}\frac{\sin t-t\cos t-1}{\cos t}=-\frac{n\pi }{2}\text{. 对}$$

于渐近线由(3.515c)给出 $y=\frac{n}{m}x-\frac{n\pi }{2}$ . 对于第二条渐近线,等等,类似地得$y=-\frac{n}{m}x+\frac{n\pi }{2}.$

3. 以显式 $y=f\left(x\right)$ 给出的函数

垂直渐近线位于函数 $f\left(x\right)$ 的无穷跳跃间断点 (参见第 76 页 2.1.5.3) 处; 水平渐近线和斜渐近线具有方程

$$\begin{array}{}\text{(3.516)}& y=kx+b,\text{ 其中 }k=\underset{x\to \mathrm{\infty }}{lim}\frac{f\left(x\right)}{x},b=\underset{x\to \mathrm{\infty }}{lim}\left[f\left(x\right)-kx\right].\end{array}$$

4. 以隐式多项式形式 $F\left(x,y\right)=0$ 给出的函数

(1)为了确定水平渐近线和垂直渐近线,我们从关于 $x$ 和 $y$ 的多项式表达式中选取次数为 $m$ 的最高次项,然后将它们分离作为函数 $\mathrm{\Phi }\left(x,y\right)$ ,并对 $x$ 和 $y$ 求解 (如果可能的话) 方程 $\mathrm{\Phi }\left(x,y\right)=0$ :

$$\begin{array}{}\text{(3.517)}& \mathrm{\Phi }\left(x,y\right)=0\text{得出}x=\phi \left(y\right),y=\psi \left(x\right)\text{.}\end{array}$$

值 $y_1=a$ ,当 $x\to \mathrm{\infty }$ 时如果极限存在则给出水平渐近线 $y=a$ ; 值 $x_1=b$ ,当 $y\to \mathrm{\infty }$ 时如果极限存在则给出垂直渐近线 $x=b$ .

(2) 为了确定斜渐近线,将直线 $y=kx+b$ 的方程代入 $F\left(x,y\right)$ ,然后按照 $x$ 的幂次排列作为结果所得的多项式:

$$\begin{array}{}\text{(3.518)}& F\left(x,kx+b\right)\equiv f_1\left(k,b\right)x^m+f_2\left(k,b\right)x^{m-1}+\cdots .\end{array}$$

从方程

$$\begin{array}{}\text{(3.519)}& f_1\left(k,b\right)=0,f_2\left(k,b\right)=0\end{array}$$

可以得到 (如果它们存在的话) 参数 $k$ 和 $b$ .

$x^3+y^3-3axy=0$ (参见第 125 页 2.11.3,图 2.59,笛卡儿叶形线). 基于方程 $F\left(x,kx+b\right)\equiv \left(1+k^3\right)x^3+3\left(k^{2}b-ka\right)x^2+\cdots$ ,根据 (3.519) 得 $f_1\left(k,b\right)=1+k^3$ $=0$ 和 $f_2\left(k,b\right)=k^{2}b-ka=0$ 并解得 $k=-1,b=-a$ ,渐近线方程是 $y=-x-a$ .

3.6.1.5 关于由一个方程给出的曲线的一般讨论

研究由方程 (3.483) $\sim \left(3.486\right)$ 之一给出的曲线通常是为了解它们的性质和形状.

1. 由显式函数 $y=f\left(x\right)$ 给出的曲线之作图

a) 确定定义域(参见第 61 页 2.1.1)

b) 确定对称性 确定曲线关于原点或 $y$ 轴的对称性以检验函数是奇函数还是偶函数 (参见第 66 页 2.1.3.4).

c) 确定函数在 $\pm \mathrm{\infty }$ 的行为 这可以通过计算 $\underset{x\to -\mathrm{\infty }}{lim}f\left(x\right)$ 和 $\underset{x\to +\mathrm{\infty }}{lim}f\left(x\right)$ 来确定 (参见第 71 页 2.1.4.7).

d) 确定间断点(参见第 76 页 2.1.5.3).

e) 确定与 $y$ 轴和 $x$ 轴的交点 这可以通过计算 $f\left(0\right)$ 和解方程 $f\left(x\right)=0$ 来确定.

f) 确定极大值和极小值并找出函数递增或递减的单调区间.

g) 确定拐点以及在这些点处的切线方程 (参见第 334 页 3.6.1.3).

我们可以利用这些数据来描绘函数的图像, 如有必要, 还可以计算一些个别点以使得绘图更加精确.

• 描绘函数 $y=\frac{2x^2+3x-4}{x^2}$ 的图像:

a) 该函数对于除 $x=0$ 外的所有 $x$ 有定义.

b) 不具有对称性.

c) 当 $x\to -\mathrm{\infty }$ 时有 $y\to 2$ ,并且显然 $y=2-0$ ,即从下方趋近,而当 $x\to \mathrm{\infty }$ 时也有 $y\to 2$ ,但 $y=2+0$ ,即从上方趋近.

**d) $x\ast \ast =0$ 是一个间断点使得函数从左边和右边都趋向 $-\mathrm{\infty }$ ,因为对于 $x$ 较小的值 $y$ 是负的.

e) 因为 $f\left(0\right)=-\mathrm{\infty }$ 成立,所以与 $y$ 轴没有交点,由 $f\left(x\right)=2x^2+3x-4=0$ 得与 $x$ 轴交点位于 $x_1\approx 0.85$ 和 $x_2\approx -2.35$ .

f) 极大值在 $x=8/3\approx 2.66$ 处取得,在此 $y\approx 2.56$ .

g) 在 $x=4,y=2.5$ 处有一个拐点,过该点的切线斜率为 $\tan \alpha =-\frac{1}{16}$ .

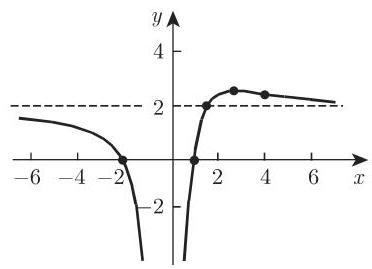
h) 在基于这些数据描绘了函数的图像 (图 3.233) 后, 我们可以计算该曲线与渐近线的交点,它位于 $x=4/3\approx 1.33$ 和 $y=2$ .

2. 由隐函数 $F\left(x,y\right)=0$ 给出的曲线之作图

对于这种情形没有一般的规则, 因为根据函数的具体形式可以采取不同的步骤. 如有可能, 我们推荐下列步骤: a) 确定与坐标轴的所有交点

b) 确定曲线的对称性 这可以通过将 $x$ 替换为 $-x$ 和 $y$ 替换为 $-y$ 来确定.

c) 确定极大值和极小值 先关于 $x$ 轴确定,然后交换 $x$ 和 $y$ 再关于 $y$ 轴确定 (参见第 596 页 6.1.5.3).

d) 确定拐点和此处的切线斜率(参见第 334 页 3.6.1.3).

e) 确定奇点(参见第 336 页3.6.1.3,3.).

f) 确定顶点(参见第 336 页 3.6.1.3, 2.) 和对应的曲率圆 (参见第 331 页 3.6.1.2, 4.). 在相对较大的一段曲线上, 常常很难区分曲线的弧段与曲率圆的圆弧段.

g) 确定渐近线的方程(参见第 338 页 3.6.1.4) 以及曲线的支相对于渐近线的位置.

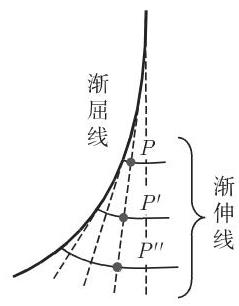
3.6.1.6 渐屈线和渐伸线

1. 渐屈线

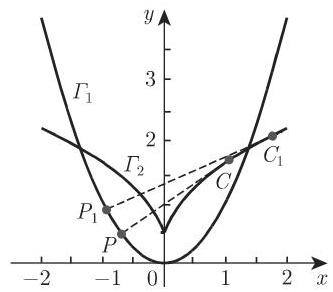
一条曲线的渐屈线是该曲线曲率中心的轨迹 (参见第 332 页 3.6.1.2, 5.); 同时它也是该曲线法线的包络 (也见第 342 页 3.6.1.7). 如果将 (3.502) (3.504) 中的 $x_C$ 和 $y_C$ 视为动点坐标,则渐屈线的参数形式可以从曲率中心的坐标公式导出. 如果有可能从 $\left(3.502\right)\sim \left(3.504\right)$ 中消去参数 $\left(x,t\text{或}\phi \right)$ ,则可以获得由笛卡儿坐标表示的渐屈线方程.

$◼$ 确定抛物线 $y=x^2$ 的渐屈线 (图 3.234). 从 $X=x-\frac{2x\left(1+4x^2\right)}{2}=-4x^3,Y=$ $x^2+\frac{1+4x^2}{2}=\frac{1+6x^2}{2}$ ,考虑 $X$ 和 $Y$ 作为动点,得渐屈线 $Y=\frac{1}{2}+3{\left(\frac{X}{4}\right)}^{2/3}$ .

2. 渐伸线或渐开线

曲线 ${\mathrm{\Gamma }}_2$ 的渐伸线 (也称为渐开线) 是一条曲线 ${\mathrm{\Gamma }}_1$ ,后者的渐屈线是 ${\mathrm{\Gamma }}_2$ . 因此, 渐伸线的每条法线 $PC$ 是渐屈线的一条切线 (图 3.234),渐屈线的弧长 $\stackrel{⏜}{C{C}_1}$ 等于渐

伸线曲率半径的增量:

$$\begin{array}{}\text{(3.520)}& {\stackrel{⏜}{CC}}_1={\overline{P_{1}C}}_1-\overline{PC}\end{array}$$

这些性质表明,渐伸线 ${\mathrm{\Gamma }}_1$ 可以看作是从 ${\mathrm{\Gamma }}_2$ 伸开的棉纱线末端描绘的曲线. 一条给定的渐屈线对应一族曲线, 其中每条曲线由棉纱线的初始长度确定 (图 3.235).

渐屈线的方程可以通过积分对应于其渐屈线的微分方程组得到. 关于圆的渐伸线方程见第 137 页 2.14.4.

$◼$ 悬链线是曳物线的渐屈线; 曳物线是悬链线的渐伸线 (参见第 139 页 2.15.1).

3.6.1.7 曲线族的包络

1. 特征点

考虑由下面方程表示的 1-参数曲线族

$$\begin{array}{}\text{(3.521)}& F\left(x,y,\alpha \right)=0.\end{array}$$

这族里相应于参数值 $\alpha$ 和 $\alpha +\mathrm{\Delta }\alpha$ 的任何两条邻近曲线具有最接近的点 $K$ . 这样一个点要么是曲线 $\left(\alpha \right)$ 和 $\left(\alpha +\mathrm{\Delta }\alpha \right)$ 的交点; 要么是曲线 $\left(\alpha \right)$ 上的一个点,它沿法线到曲线 $\left(\alpha +\mathrm{\Delta }\alpha \right)$ 的距离是比 $\mathrm{\Delta }\alpha$ 更高阶的无穷小量 (图 3.236(a),(b)). 当 $\mathrm{\Delta }\alpha \to 0$ 时曲线 $\left(\alpha +\mathrm{\Delta }\alpha \right)$ 趋近于曲线 $\left(\alpha \right)$ ,其中在某些情形点 $K$ 趋于一个极限位置,即特征点.

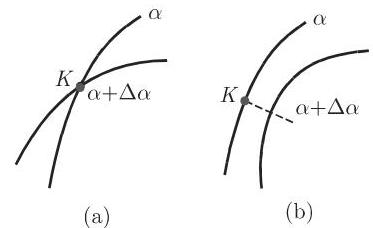
2. 曲线族特征点的几何轨迹

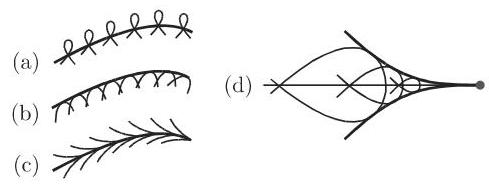
方程 (3.521) 可以表示一条或多条曲线. 它们由最接近的点或该曲线族的边界点形成 (图 3.237(a)), 或者说它们形成了该曲线族的包络, 即与族中每条曲线相切的一条曲线 (图 3.237(b)). 也有可能是这两种情形的组合 (图 3.237(c), (d)).

3. 包络的方程

包络的方程可以从 (3.521) 计算,其中 $\alpha$ 可以从下列方程组中消去:

$$\begin{array}{}\text{(3.522)}& F=0,\frac{\partial F}{\partial \alpha }=0.\end{array}$$

$◼$ 确定当长为 $\left|AB\right|=l$ 的线段 $AB$ 的端点沿坐标轴滑动时所产生的直线族的方程 (图 3.238(a)). 曲线族的方程是

$$\frac{x}{l\sin \alpha }+\frac{y}{l\cos \alpha }=1$$

或 $F\equiv x\cos \alpha +y\sin \alpha -l\sin \alpha \cos \alpha =0,\frac{\partial F}{\partial \alpha }=-x\sin \alpha +y\cos \alpha -l{\cos }^2\alpha +$ $l{\sin }^2\alpha =0$ . 消去 $\alpha$ 给出作为包络的 $x^{2/3}+y^{2/3}=l^{2/3}$ ,它是一条星形线 (也见图 3.238(b)).