Appearance
15.2.2 到原始空间的逆变换
为进行逆变换, 有下述可能方法:
(1) 使用对应表, 即原函数和积分相对应的表格 (参见第 1431 页表 21.13).
(2) 利用变换的一些性质, 约化为已知的对应 (参见第 1018 页 15.2.2.2 和 1019 页 15.2.2.3).
(3) 借助反演公式 (参见第 1020 页 15.2.2.4).
15.2.2.1 借助表格求逆变换
通过第 1431 页表 21.13 的例子说明对表格的使用.
更多表格可见 [15.3].
运用卷积定理 (15.23) 得到
15.2.2.2 部分分式分解
1. 原则
在很多应用中,有形如
2.
若变换
对应的原函数是
3. 赫维赛德展开定理
若分子
4. 复根
即使在分母有复根的情况, 也同样可以使用赫维赛德展开定理. 对应共轭复根的项可以合并为一个二次表达式, 其逆变换也可在关于高阶重根的表格中找到.
或通过使用部分分式分解和表格, 可得到
15.2.2.3 级数展开
为了根据
1.
当
其中值
2.
若
此处,
当
在某些情况下,比如,当亚纯函数
15.2.2.4 逆积分
反演公式
表示特定区域内解析函数的复积分. 复函数积分理论可使用的积分方法此时都可以应用, 比如, 留数计算或根据柯西积分定理对积分路径进行变化.
- 由于
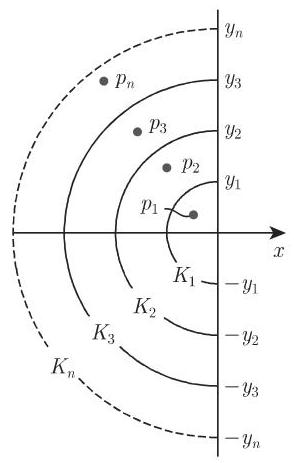
是双值函数. 因此,我们选择下述积分路径 (图 15.20):
根据若尔当引理 (参见第 986 页 14.4.3),当
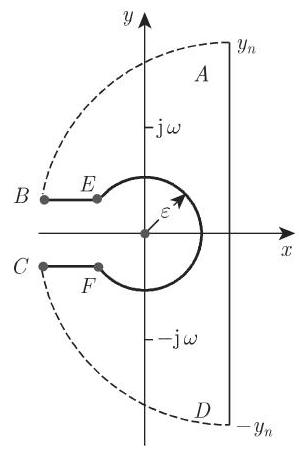
最终可得