Appearance
19.5.1 差分法
通过选取点
当
(19.138)
偏导数 | 有限差分 | 误差阶 |
(19.137)
更实用. 公式 (19.138) 表示由相应于
由公式 (19.137) 偏微分方程可以在网格的每个内点写成差分方程, 这里同样考虑其边值条件与初值条件. 对于小的步长
其解为
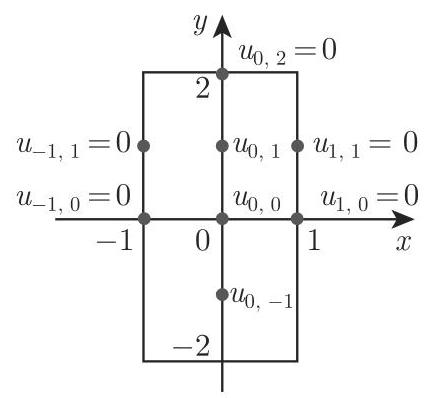
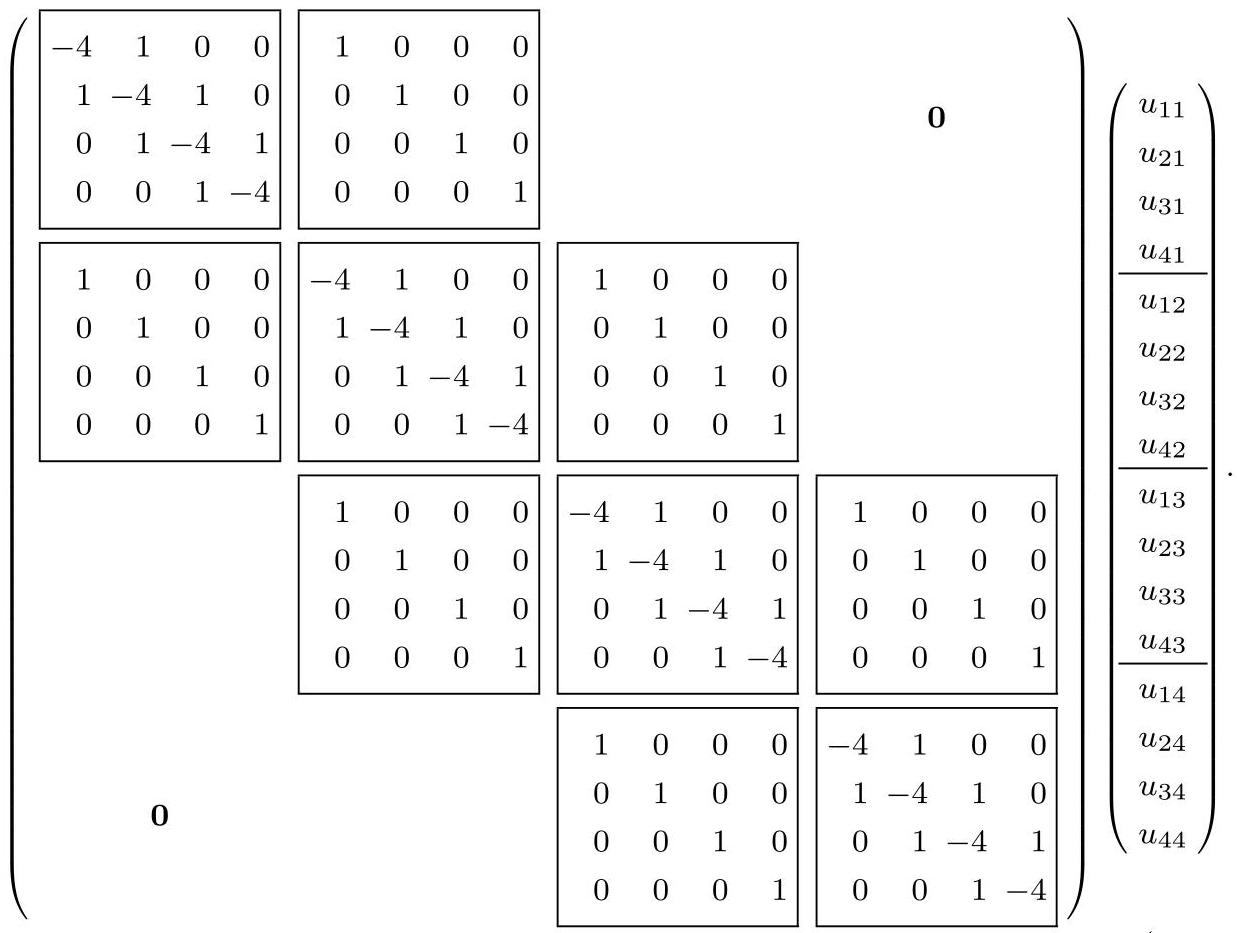
(19.139)
系数矩阵是对称稀疏的. 这个形式称为块三对角矩阵. 显然矩阵的形式依赖于网格
Appearance
通过选取点
当
(19.138)
偏导数 | 有限差分 | 误差阶 |
(19.137)
更实用. 公式 (19.138) 表示由相应于
由公式 (19.137) 偏微分方程可以在网格的每个内点写成差分方程, 这里同样考虑其边值条件与初值条件. 对于小的步长
其解为


(19.139)
系数矩阵是对称稀疏的. 这个形式称为块三对角矩阵. 显然矩阵的形式依赖于网格