Appearance
4.6.3 奇异值分解
(1) 奇异值和奇异向量 设
左右奇异向量间的关系是
秩为
(参见第 368 页 4.1.4, 9.).
(2) 奇异值分解 表达式
称为矩阵
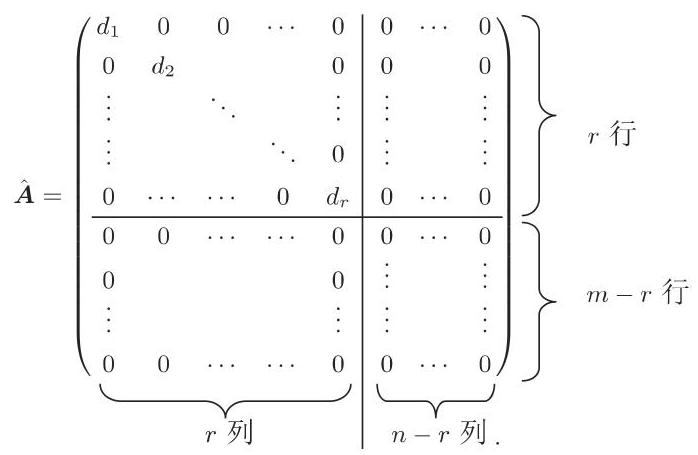
矩阵
注 用
(3) 应用 奇异值分解可用来确定大小为(m, n)的矩阵
其中
Appearance
(1) 奇异值和奇异向量 设
左右奇异向量间的关系是
秩为
(参见第 368 页 4.1.4, 9.).
(2) 奇异值分解 表达式
称为矩阵

矩阵
注 用
(3) 应用 奇异值分解可用来确定大小为(m, n)的矩阵
其中