Appearance
14.1.3 共形映射
14.1.3.1 共形映射的概念和性质
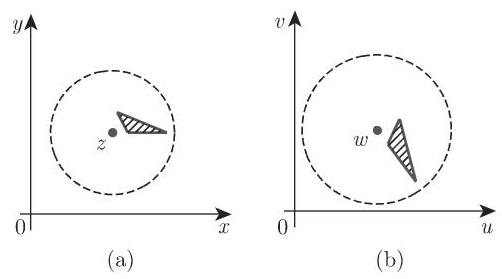
1. 定义
一个从
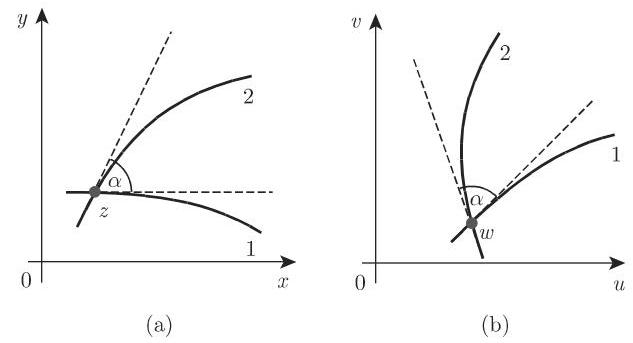
共形映射有下述一些性质:
线元
注 共形映射出现在物理学、电工学、流体动力学、空气动力学和其他的数学领域中.
2. 柯西-黎曼方程组
所给出, 该变换用矩阵形式表为
根据柯西-黎曼微分方程组,
3. 正交系
① 为了把柯西-黎曼方程组的两个方程放在一起, 改变了 (14.10c) 和 (14.10d) 的次序. ——译者注
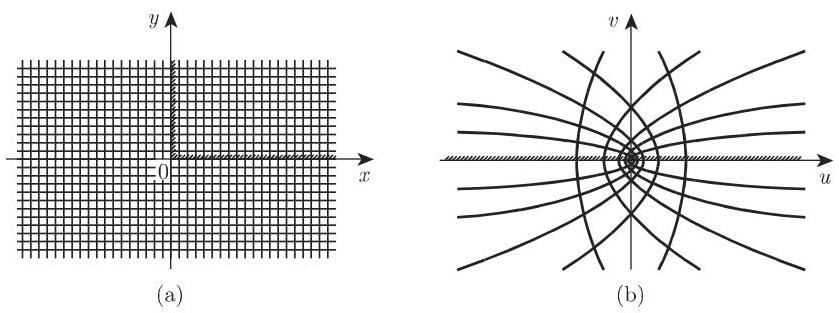
14.1.3.2 最简单的一些共形映射
在这一节中,将讨论一些变换及其最重要的性质,并且在
1. 线性函数
对于以线性函数形式
给出的共形映射, 可以分 3 步完成其变换:
a)
b)
c)
总之,
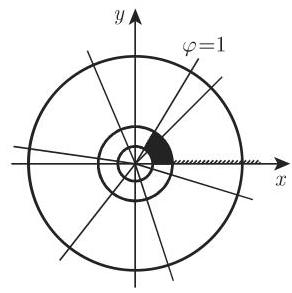
2. 反演
共形映射
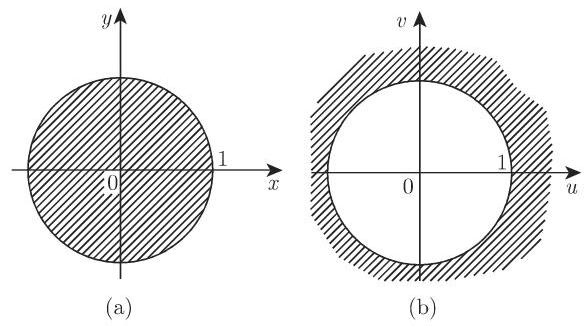
表示关于单位圆周 (unit circle) 的一个反演 (inversion) 以及对实轴的一个镜射, 即
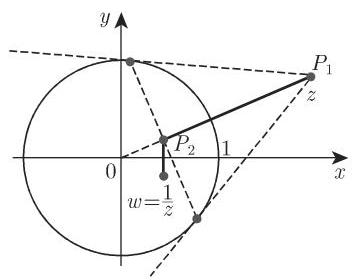
注 一般地,一个几何变换被称为关于一个半径为
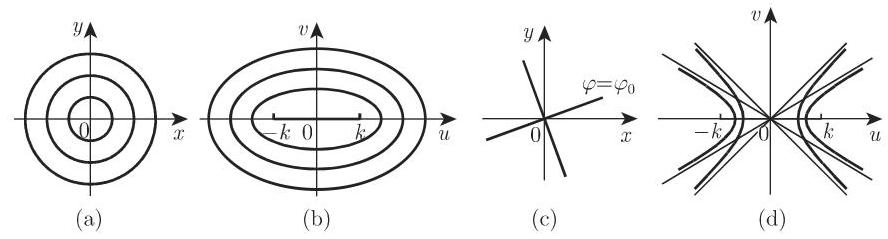
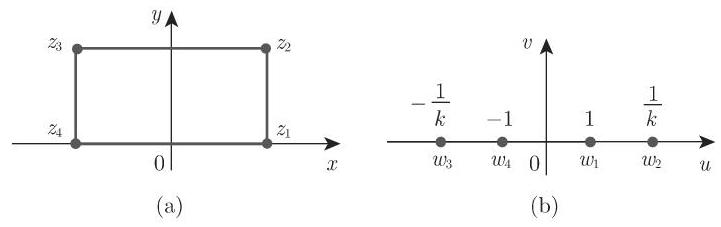
3. 线性分式函数
对于以线性分式函数形式
给出的共形映射, 可以分 3 步实现其变换:
a) 线性函数:
b) 反演:
c) 线性函数 :
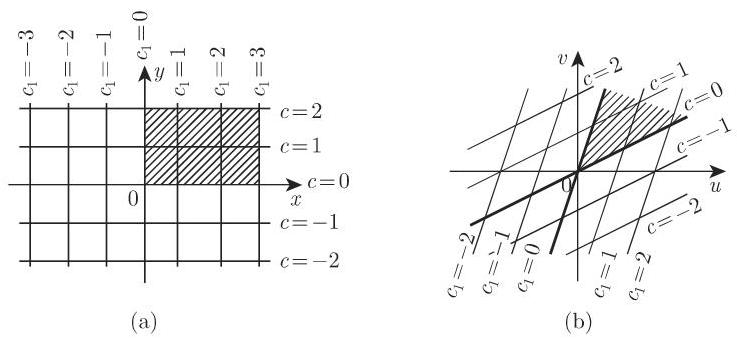
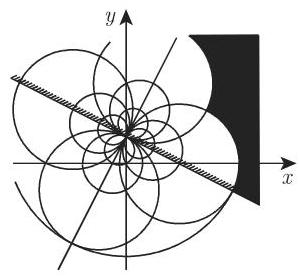
的两个点. 如果点
有正交笛卡儿网为其像的正交网被表示在图 14.12 中.
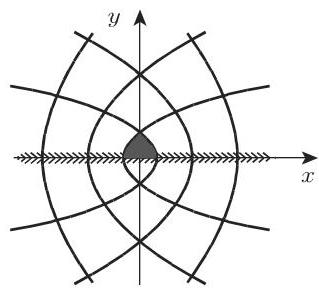
4. 二次函数
由二次函数
描述的共形映射有极坐标形式
并可作为
从极坐标表达式显然可知,
在笛卡儿坐标中的表达式表明,
这个映射的不动点是
5. 平方根
以
给出的共形映射把整个
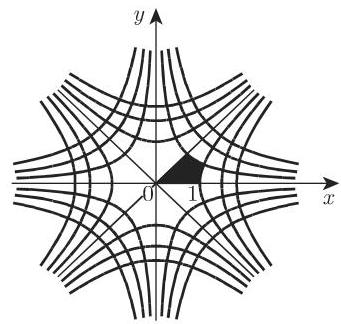
这个映射的不动点是
6. 线性与分式线性函数之和
用函数
给出的共形映射,根据 (14.8),以极坐标表示
其焦点是实轴上的点
是双值的.
相应于
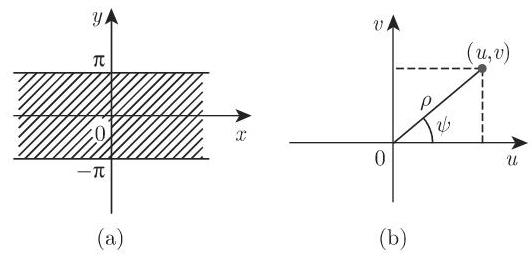
7. 对数
用对数函数形式
给出的共形映射当
从这个表达式即知,坐标线
对数函数
局限于考察
8. 指数函数
用指数函数形式 (亦见第 990 页 14.5.2,1.)
给出的共形映射在极坐标中有形式
从
如果
9. 施瓦茨-克里斯托费尔 (Christoffel) 公式
由施瓦茨-克里斯托费尔公式
复常数
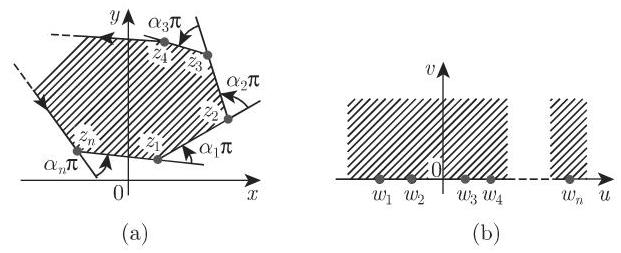
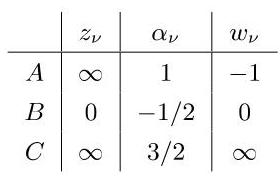
为了确定
考虑到映射对应 “
考虑到映射对应 “
14.1.3.3 施瓦茨反射原理
1. 叙述
假设
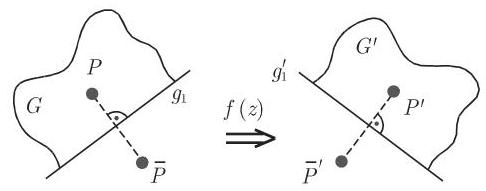
2. 应用
这个原理的应用使得施行运算以及具有直线边界平面区域的表示变得容易了: 如果直线边界是一条流线 (图 14.22 中的孤立边界), 那么源被反射为源, 汇被反射为汇, 并且旋度被反射为相反旋转方向的旋度. 如果直线边界是一条位势线 (图 14.23 中的高导电边界), 那么源被反射为汇, 汇被反射为源, 并且旋度被反射为相同旋转方向的旋度.
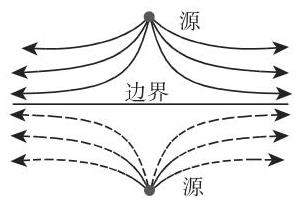
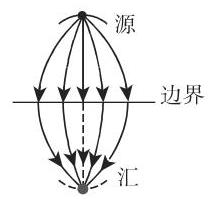
14.1.3.4 复位势
1. 复位势的概念
考虑
a) 无源场
的可积性条件, 因而有
对于场
b) 无旋场
的可积性条件, 因而有
如果场既是无源的,又是无旋的,那么函数
那么这个函数被称为场
此时,在物理学和电工学中通常记号意义下 (参见第 941 页 13.3.1.6,2.)
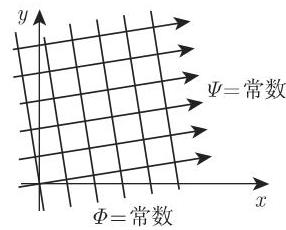
2. 齐次场的复位势
当
是一个场的复位势,该场的位势线平行于
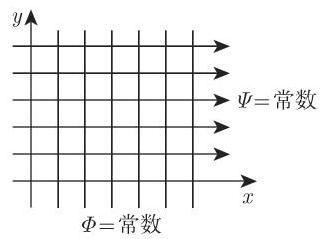
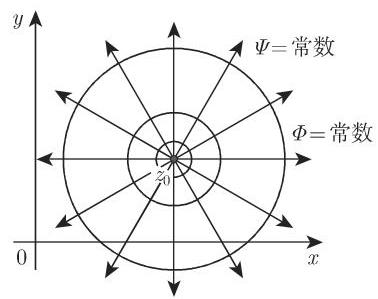
3. 源与汇的复位势
在点
在点
方向线从
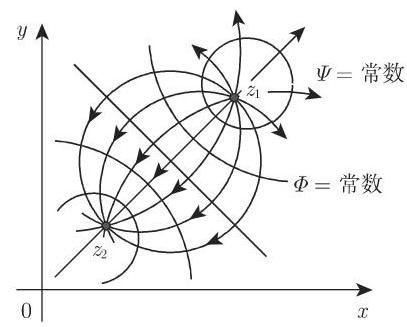
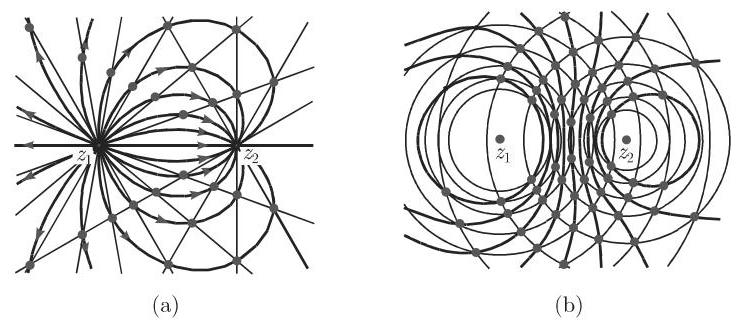
4. 源一汇系统的复位势
对于在点
位势线
5. 偶极子的复位势
一个在
6. 旋度的复位势
如果旋度的强度是
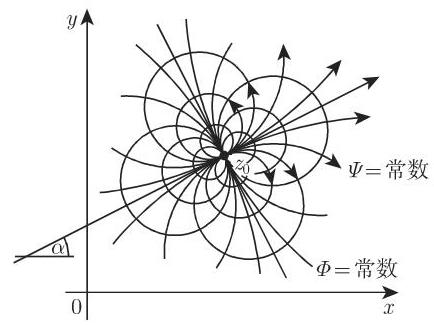
与图 14.26 比较,方向线和位势线的作用互换了. 对于复的
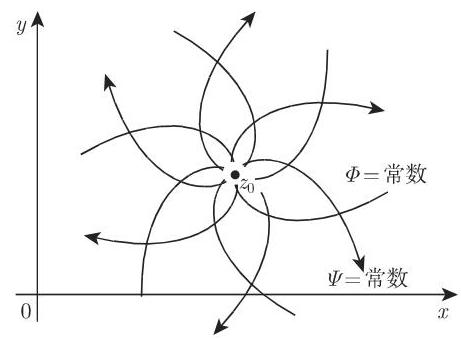
14.1.3.5 叠加原理
1. 复位势的叠加
一个由一些源、汇和旋度组成的系统是一些单个场的叠加, 即通过把它们的复位势和流函数相加而得到该系统的函数. 由于拉普拉斯微分方程
2. 向量场的合成
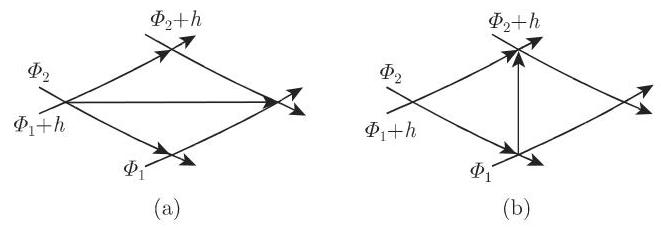
(1)积分 除了把复位势相加以外, 还可以通过应用于权函数的积分来构作新的场.
其中
(2) 麦克斯韦 (Maxwell) 对角线方法 如果想做具有位势
强度商为
14.1.3.6 复平面的任意映射
函数
被定义,如果实变量的两个函数
a) 坐标线的变换
b) 几何图形的变换
c) 黎曼曲面 对于几个不同的