Appearance
19.1.2 多项式方程的解
为求有效解需要这些函数值
19.1.2.1 霍纳格式
1. 实数情况
为通过
这里
递推公式
可以根据 (19.12) 对比
即得到多项式序列
... | ||||||||
... | ||||||||
... | ||||||||
... | ||||||||
... | ||||||||
(19.16)
从格式 (19.16) 得到多项式的值
(19.17)
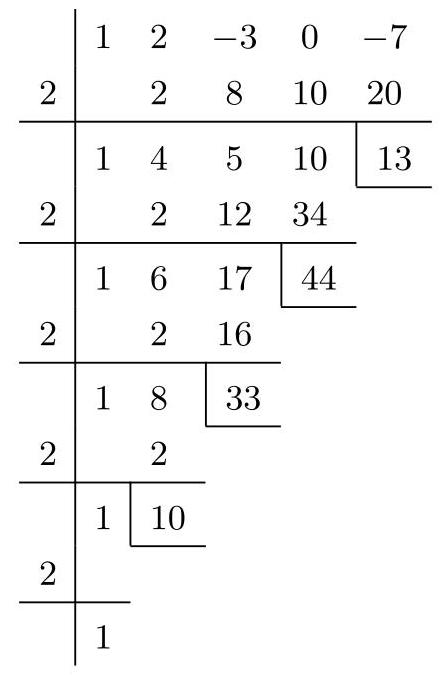
可得
注 (1) 多项式
(2) 霍纳格式也可以用来计算复系数
2. 复数情况
如果 (19.11) 中的系数
其中
于是
为得到 (19.18a) 科拉茨 (Collatz) 引进所谓双列霍纳格式 (two-row Horner scheme), 其构造如下:(19.18d)
19.1.2.2 根的位置
1. 实根、斯图姆序列
笛卡儿符号法则给出了多项式方程 (19.11) 是否有实根的原始思想.
a) 正实根的个数等于系数序列
改变符号的次数, 或扣除一个偶数.
b) 负实根的个数等于系数序列
改变符号的次数, 或扣除一个偶数.
2. 复根
为了在有界复平面区域上限定实数根或者复数根的位置, 考察如下多项式方程, 这是 (19.11) 的简单推广:
通过系统的重复试错,对 (19.20) 的正根决定一个上界
据此有
注 为确定带负实部的复根个数, 在电子技术所谓根轨迹理论中发展了一种特别的方法, 该方法可用来检验稳定性 (见 [19.14][19.40]).
19.1.2.3 数值方法
1. 一般方法
在 19.1.1 讨论的方法可用来求多项式方程的实数根. 牛顿法由于其快速收敛性以及函数值
迭代修正
2. 特殊方法
贝尔斯托 (Bairstow) 法常用于求成对的根, 尤其是成对的共轭复根. 该方法类似于霍纳格式
如果需要计算根的绝对值的最大值与最小值, 可以选择使用伯努利方法 (见[19.38]).
格雷费 (Graeffe) 法有某些历史重要性. 它同时给出包括复共轭根在内的所有的根; 然而其计算量非常巨大 ([19.14],[19.40]).