3.1.2 圆函数与双曲函数的几何定义

3.1.2.1 圆函数或三角函数的定义

1. 用单位圆定义

一个角 $\alpha$ 的三角函数是就半径 $R=1$ 的单位圆和一个直角三角形的锐角 (图 3.5(a),(b)) 借助邻边 $b$ 、对边 $a$ 和斜边 $c$ 来定义的. 在单位圆中一个角的度量由一条固定半径 $\overline{OA}$ (长度 1) 和一条逆时针 (正向) 移动的半径 $\overline{OC}$ 做成:

正弦: $\sin \alpha =\overline{BC}=\frac{a}{c}$ ,(3.3)

余弦: $\cos \alpha =\overline{OB}=\frac{b}{c}$ ,(3.4)

正切: $\tan \alpha =\overline{AD}=\frac{a}{b}$ ,(3.5)

余切 $:\cot \alpha =\overline{EF}=\frac{b}{a}$ ,(3.6)

正割: $\sec \alpha =\overline{OD}=\frac{c}{b}$ ,(3.7)

余割: $\csc \alpha =\overline{OF}=\frac{c}{a}$ .(3.8)

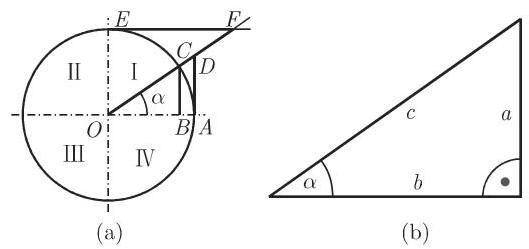
2. 三角函数的符号

依赖于移动的半径 $\overline{OC}$ 所在单位圆的象限 (图 3.5(a)),这些函数具有唯一定义的符号, 它们可以从表 2.2(见第 101 页) 中确定.

3. 由扇形面积给出的三角函数定义

函数 $\sin \alpha ,\cos \alpha ,\tan \alpha$ 定义为 $R=1$ 的单位圆的线段 $\overline{BC},\overline{OB},\overline{AD}$ (图 3.6), 其中自变量是圆心角 $\alpha =\mathrm{\$}AOC$ . 对于这个定义我们也可以使用扇形 $COK$ 的面积 $t$ ,它表示为图 3.6 中的阴影面积. 使用以弧度度量的圆心角 $2\alpha$ ,对于 $R=1$ 我们得到其面积 $t=\frac{1}{2}{R}^{2}2\alpha =\alpha$ . 因此,我们有如同在 $\left(3.3\right)\sim \left(3.5\right)$ 中一样的等式 $\sin t=\overline{BC},\cos t=\overline{OB},\tan t=\overline{AD}$ .

3.1.2.2 双曲函数的定义

为了与 (3.3)-(3.5) 中三角函数的定义作类比,现以方程为 $x^2-y^2=1$ 的双曲线 (仅使用图 3.7 中右边一支) 的相应弧三角形面积代替方程为 $x^2+y^2=1$ 的单位圆的扇形面积. 用 $t$ 表示 $COK$ 的面积,即图 3.7 中的阴影面积,双曲函数的定义等式为

$$\begin{array}{}\text{(3.9)}& \sinh t=\overline{BC},\end{array}$$$$\begin{array}{}\text{(3.10)}& \cosh t=\overline{OB},\end{array}$$$$\begin{array}{}\text{(3.11)}& \tanh t=\overline{AD}\text{.}\end{array}$$

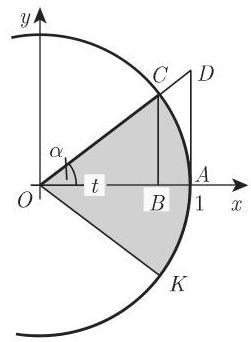
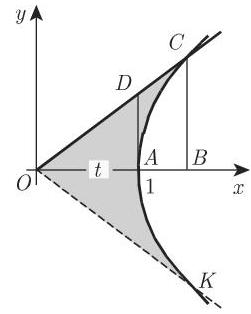
利用积分计算面积 $t$ ,并将结果用 $\overline{BC},\overline{OB}$ 和 $\overline{AD}$ 表示,得

$$\begin{array}{}\text{(3.12)}& t=\ln \left(\overline{BC}+\sqrt{{\overline{BC}}^2+1}\right)=\ln \left(\overline{OB}+\sqrt{{\overline{OB}}^2-1}\right)=\frac{1}{2}\ln \frac{1+\overline{AD}}{1-\overline{AD}},\end{array}$$

于是, 从现在起, 双曲函数可以用指数函数表示成

$$\begin{array}{}\text{(3.13a)}& \overline{BC}=\frac{{\mathrm{e}}^t-{\mathrm{e}}^{-t}}{2}=\sinh t,\end{array}$$$$\begin{array}{}\text{(3.13b)}& \overline{OB}=\frac{{\mathrm{e}}^t+{\mathrm{e}}^{-t}}{2}=\cosh t,\end{array}$$$$\begin{array}{}\text{(3.13c)}& \overline{AD}=\frac{{\mathrm{e}}^t-{\mathrm{e}}^{-t}}{{\mathrm{e}}^t+{\mathrm{e}}^{-t}}=\tanh t.\end{array}$$

这些等式所表示的是双曲函数最广为人知的定义.