13.3.1 向量场中的线积分和位势

13.3.1.1 向量场中的线积分

1. 定义

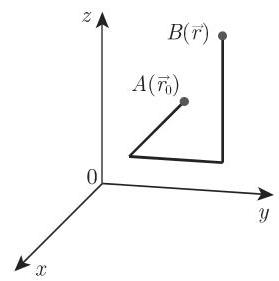
一个向量函数 $\overrightarrow{V}\left(\overrightarrow{r}\right)$ 沿一条可求长曲线 $\stackrel{⏜}{AB}$ (图 13.13) 的标量值线积分或线积分是标量值

$$\begin{array}{}\text{(13.99a)}& P={\int }_{\stackrel{⏜}{AB}}\overrightarrow{V}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{r}\end{array}$$

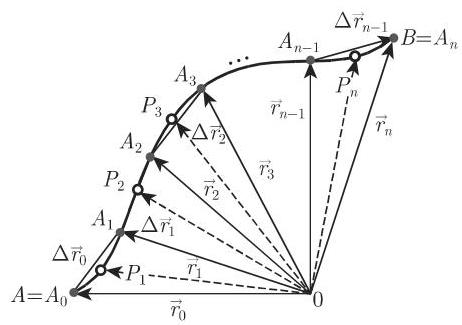
2. 5个步骤计算这个积分

a) 用分点 $A_1\left({\overrightarrow{r}}_1\right),A_2\left({\overrightarrow{r}}_2\right),\cdots ,A_{n-1}\left({\overrightarrow{r}}_{n-1}\right)\left(A=A_0,B=A_n\right)$ 把路径 $\stackrel{⏜}{AB}$ 分成 $n$ 个小弧段 (图 13.13),用向量 ${\overrightarrow{r}}_i-{\overrightarrow{r}}_{i-1}=\mathrm{\Delta }{\overrightarrow{r}}_{i-1}$ 来逼近这些弧.

b) 在每个小弧段的内部或边界任意选取位置向量为 ${\overrightarrow{\xi }}_i$ 的点 $P_i$ .

c) 在这些所选取的点处计算函数值 $\overrightarrow{V}\left({\overrightarrow{\xi }}_i\right)$ 与相应的 $\mathrm{\Delta }{\overrightarrow{r}}_{i-1}$ 的内积.

d) 取所有 $n$ 个积之和.

e) 当 $\left|△{\overrightarrow{r}}_{i-1}\right|\to 0$ 时,显然亦当 $n\to \mathrm{\infty }$ 时计算和 $\sum _{i=1}^n\tilde{\overrightarrow{V}}\left({\overrightarrow{\xi }}_i\right)\cdot \mathrm{\Delta }{\overrightarrow{r}}_{i-1}$ 的极限.

如果这个极限与诸点 $A_i$ 和 $P_i$ 的选取无关,则它被称为线积分

$$\begin{array}{}\text{(13.99b)}& {\int }_{\stackrel{⏜}{AB}}\overrightarrow{V}\cdot \mathrm{d}\overrightarrow{r}=\underset{\begin{array}{c}\left|△{\overrightarrow{r}}_{i-1}\right|\to 0\\ n\to \mathrm{\infty }\end{array}}{lim}\sum _{i=1}^n\tilde{\overrightarrow{V}}\left({\overrightarrow{\xi }}_i\right)\cdot △{\overrightarrow{r}}_{i-1}.\end{array}$$

线积分 (13.99a),(13.99b) 存在性的一个充分条件是,向量函数 $\overrightarrow{V}\left(\overrightarrow{r}\right)$ 和曲线 $\stackrel{⏜}{AB}$ 是连续的,并且曲线有连续改变的切线. 一个向量函数 $\overrightarrow{V}\left(\overrightarrow{r}\right)$ 是连续的,如果其分量, 3 个标量函数是连续的.

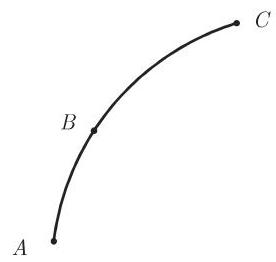
13.3.1.2 力学中线积分的解释

如果 $\overrightarrow{V}\left(\overrightarrow{r}\right)$ 是一个力场,即 $\overrightarrow{V}\left(\overrightarrow{r}\right)=\overrightarrow{F}\left(\overrightarrow{r}\right)$ ,则线积分 (13.99a) 表示当一个粒子 $m$ 沿路径 $\stackrel{⏜}{AB}$ 移动时 $\overrightarrow{F}$ 所做的功 (见第 939 页图 13.13,图 13.14).

13.3.1.3 线积分的性质

$$\begin{array}{}\text{(13.100)}& {\int }_{\stackrel{⏜}{ABC}}\overrightarrow{V}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{r}={\int }_{\stackrel{⏜}{AB}}\overrightarrow{V}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{r}+{\int }_{\stackrel{⏜}{BC}}\overrightarrow{V}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{r}\text{(图13.14),}\end{array}$$$$\begin{array}{}\text{(13.101)}& {\int }_{\stackrel{⏜}{AB}}\overrightarrow{V}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{r}=-{\int }_{\stackrel{⏜}{BA}}\overrightarrow{V}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{r},\end{array}$$$$\begin{array}{}\text{(13.102)}& {\int }_{\stackrel{⏜}{AB}}\left[\overrightarrow{V}\left(\overrightarrow{r}\right)+\overrightarrow{W}\left(\overrightarrow{r}\right)\right]\cdot \mathrm{d}\overrightarrow{r}={\int }_{\stackrel{⏜}{AB}}\overrightarrow{V}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{r}+{\int }_{\stackrel{⏜}{AB}}\overrightarrow{W}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{r},\end{array}$$$$\begin{array}{}\text{(13.103)}& {\int }_{\stackrel{⏜}{AB}}c\overrightarrow{V}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{r}=c{\int }_{\stackrel{⏜}{AB}}\overrightarrow{V}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{r}\text{ (}c\text{为常数). }\end{array}$$

13.3.1.4 笛卡儿坐标系中的线积分

在笛卡儿坐标系中下述公式成立:

$$\begin{array}{}\text{(13.104)}& {\int }_{\stackrel{⏜}{AB}}\overrightarrow{V}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{r}={\int }_{\stackrel{⏜}{AB}}\left(V_x\mathrm{d}x+V_y\mathrm{d}y+V_z\mathrm{d}z\right).\end{array}$$

13.3.1.5 沿向量场中一条闭曲线的积分

一个线积分被称为周线积分 (contour integral), 如果积分路径是一条闭曲线. 如果标量积分值用 $P$ 表示,闭曲线用 $C$ 表示,则用下述记号:

$$\begin{array}{}\text{(13.105)}& P={\oint }_C\overrightarrow{V}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{r}\end{array}$$

13.3.1.6 保守场或位势场

1. 定义

如果一个向量场中的线积分 (13.99a) 的值 $P$ 仅依赖于初始点 $A$ 和终点 $B$ ,而与连接它们的路径无关, 则该场被称为保守场 (conservative field) 或位势场 (pota-tial field). 在保守场中的周线积分之值恒为零:

$$\begin{array}{}\text{(13.106)}& {\oint }_C\overrightarrow{V}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{r}=0.\end{array}$$

保守场总是无旋的:

$$\begin{array}{}\text{(13.107)}& \mathrm{rot}\overrightarrow{V}=\overrightarrow{0}\end{array}$$

并且反之, 此等式是一个向量场成为保守场的一个充分条件. 当然, 必须假设场函数 $\overrightarrow{V}$ 关于相应的坐标的偏导数是连续的,并且 $\overrightarrow{V}$ 的定义域是单连通的. 这个条件也称为可积性条件 (integrability condition) (参见第 692 页 8.3.4.2), 它在笛卡儿坐标系中有下述形式

$$\begin{array}{}\text{(13.108)}& \frac{\partial V_x}{\partial y}=\frac{\partial V_y}{\partial x},\frac{\partial V_y}{\partial z}=\frac{\partial V_z}{\partial y},\frac{\partial V_z}{\partial x}=\frac{\partial V_x}{\partial z}.\end{array}$$

2. 保守场的位势

一个保守场的位势, 或者其位势函数, 是标量函数

$$\begin{array}{}\text{(13.109a)}& U\left(\overrightarrow{r}\right)={\int }_{{\overrightarrow{r}}_0}^{\overrightarrow{r}}\overrightarrow{V}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{r}.\end{array}$$

在保守场中,它作为具有一个固定初始点 $A\left({\overrightarrow{r}}_0\right)$ 和一个变动终点 $B\left(\overrightarrow{r}\right)$ 的线积分来计算

$$\begin{array}{}\text{(13.109b)}& U\left(\overrightarrow{r}\right)={\int }_{\stackrel{⏜}{AB}}\overrightarrow{V}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{r}.\end{array}$$

注 在物理学中,一个函数 $\overrightarrow{V}\left(\overrightarrow{r}\right)$ 的位势 $U^{\ast }\left(\overrightarrow{r}\right)$ 经常被认为有相反的符号

$$\begin{array}{}\text{(13.110)}& U^{\ast }\left(\overrightarrow{r}\right)=-{\int }_{{\overrightarrow{r}}_0}^{\overrightarrow{r}}\overrightarrow{V}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{r}=-U\left(\overrightarrow{r}\right).\end{array}$$

3. 梯度、线积分和位势之间的关系

如果关系式 $\overrightarrow{V}\left(\overrightarrow{r}\right)=\mathrm{grad}U\left(\overrightarrow{r}\right)$ ,则 $U\left(\overrightarrow{r}\right)$ 是场 $\overrightarrow{V}\left(\overrightarrow{r}\right)$ 的位势,并且反之, $\overrightarrow{V}\left(\overrightarrow{r}\right)$ 是保守场或位势场. 在物理学中, 相应于 (13.110), 经常用相反的符号.

4. 保守场中位势的计算

如果在笛卡儿坐标系中给定函数 $\overrightarrow{V}\left(\overrightarrow{r}\right)=V_x\overrightarrow{i}+V_y\overrightarrow{j}+V_z\overrightarrow{k}$ ,则其位势函数 $U$ 的全微分为

$$\begin{array}{}\text{(13.111a)}& \mathrm{d}U=V_x\mathrm{d}x+V_y\mathrm{d}y+V_z\mathrm{d}z.\end{array}$$

这里,系数 $V_x,V_y,V_z$ 必须满足可积性条件 (13.108). 从方程组

$$\begin{array}{}\text{(13.111b)}& \frac{\partial U}{\partial x}=V_x,\frac{\partial U}{\partial y}=V_y,\frac{\partial U}{\partial z}=V_z\end{array}$$

即得 $U$ . 在实践中,可以通过沿 3 段平行于坐标轴并相连的直线段 (图 13.15) 的积分来计算位势:

$$U={\int }_{{\overrightarrow{r}}_0}^{\overrightarrow{r}}\overrightarrow{V}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{r}=U\left(x_0,y_0,z_0\right)+{\int }_{x_0}^x{V}_x\left(x,y_0,z_0\right)\mathrm{d}x$$$$\begin{array}{}\text{(13.112)}& +{\int }_{y_0}^y{V}_y\left(x,y,z_0\right)\mathrm{d}y+{\int }_{z_0}^z{V}_z\left(x,y,z\right)\mathrm{d}z.\end{array}$$