Appearance
5.8.2 无向图的遍历
5.8.2.1 边序列或路
1. 边序列或路
在一个无向图
称作长
如果
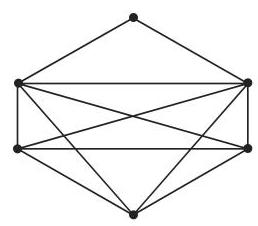
在图 5.38 中,
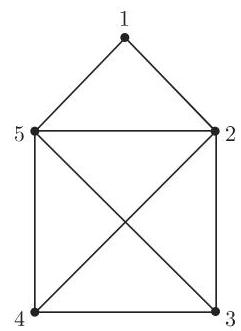
2. 连通图、分量
如果在图
3. 顶点间的距离
无向图中两个顶点
4. 最短路问题
设
有一个解决此问题的丹齐格有效算法, 它是对有向图叙述的, 并且也可类似地应用于无向图 (参见第 551 页 5.8.6).
每个图
在每条边的权都为 1 的情形,即
存在从顶点
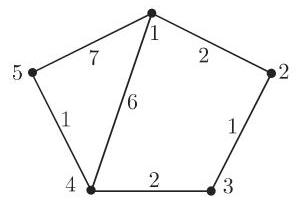
图 5.39 中给出的加权图有距离矩阵
图 5.40 中给出的图有关联矩阵
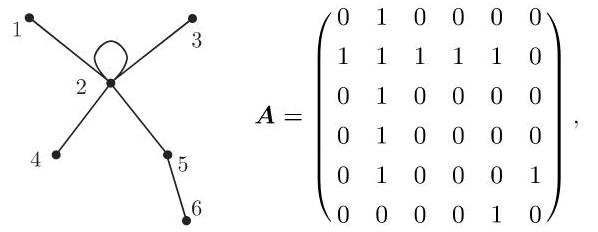
5.8.2.2 欧拉迹
1. 欧拉迹、欧拉图
含有图
含有闭欧拉迹的连通图是一个欧拉图.
图
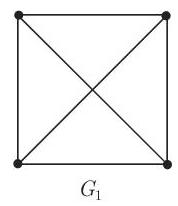
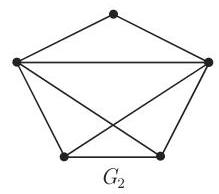
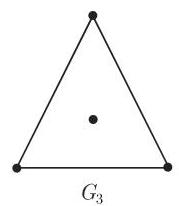
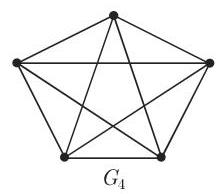
2. 欧拉-希尔霍尔策 (Euler-Hierholzer) 定理
有限连通图是欧拉图, 当且仅当它的所有顶点的次数都是正偶数.
3. 闭欧拉迹的构造
如果
4. 开欧拉迹
图
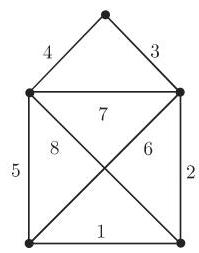
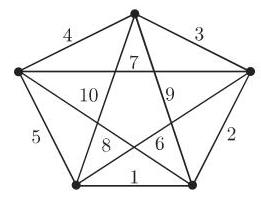
5. 中国邮递员问题
问题是: 邮递员必须至少一次通过他的服务区的所有街道且回到出发地, 并且要使路程尽可能短; 这个问题可以用图论术语叙述如下: 设
这个问题的命名源于中国数学家管梅谷, 他首先研究此问题. 为解此问题要区分两种情形:
(1)
(2)
解这个问题的一个有效算法是埃德蒙兹 (Edmonds) 和约翰逊 (Johnson) 给出的 (见 [5.49]).
5.8.2.3 哈密顿圈
1. 哈密顿圈
哈密顿圈是覆盖图中所有顶点的基本圈.
在图 5.47 中, 粗线条表示一个哈密顿圈.
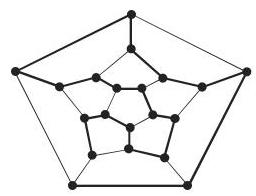
在面为五边形的十二面体的图中构造哈密顿圈游戏的想法可以追溯到哈密顿爵士.
注 刻画有哈密顿圈的图的问题导致一个经典的 NP 完全问题. 因此在此不能给出确定哈密顿圈的有效算法.
2. 狄拉克定理
如果简单图
图 5.48 给出一个图, 它有一个哈密顿圈, 但并不满足下述奥尔定理的假设.
3. 奥尔 (Ore) 定理
如果简单图
4. 波萨 (Posa) 定理
设简单图
(1) 对于
(2) 若