Appearance
11.5.1 阿贝尔积分方程
把积分方程对物理问题的首批应用之一是由阿贝尔 (Abel) 考虑的. 一个质点在一个铅垂平面中沿着一条曲线,仅在重力影响下从点
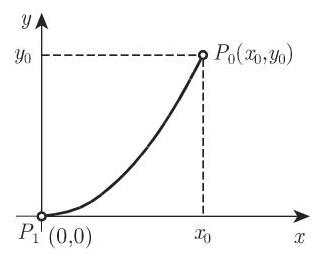
质点在曲线一个点处的速度是
下落时间作为
如果
下一个问题是当下落时间被给定后,作为
并改变记号,把
现在考虑稍微一般的方程
当
乘以
改变左端的积分次序, 得到
可以用代换
将此结果代入 (11.71b). 在关于
Appearance
把积分方程对物理问题的首批应用之一是由阿贝尔 (Abel) 考虑的. 一个质点在一个铅垂平面中沿着一条曲线,仅在重力影响下从点

质点在曲线一个点处的速度是
下落时间作为
如果
下一个问题是当下落时间被给定后,作为
并改变记号,把
现在考虑稍微一般的方程
当
乘以
改变左端的积分次序, 得到
可以用代换
将此结果代入 (11.71b). 在关于