5.9.2 模糊集的连接 (聚合)

模糊集可以通过算子加以聚合. 对于怎样将通常的集合运算加以推广, 如模糊集的并、交及补, 有几个不同的建议.

5.9.2.1 模糊集的聚合概念

1. 模糊集并、模糊集交

集合 $A\cup B$ 和 $A\cap B$ 中的任意元素 $x\in X$ 的隶属等级应该只与两个模糊集 $A$ 和 $B$ 中元素的隶属等级 ${\mu }_A\left(x\right)$ 和 ${\mu }_B\left(x\right)$ 有关. 模糊集的并和交借助两个函数

$$\begin{array}{}\text{(5.343)}& s,t:\left[0,1\right]\times \left[0,1\right]\to \left[0,1\right]\end{array}$$

定义, 并且它们用下列方式定义:

$$\begin{array}{}\text{(5.344)}& {\mu }_{A\cup B}\left(x\right)\text{:=}s\left({\mu }_A\left(x\right),{\mu }_B\left(x\right)\right),\end{array}$$$$\begin{array}{}\text{(5.345)}& {\mu }_{A\cap B}\left(x\right)\text{:=}t\left({\mu }_A\left(x\right),{\mu }_B\left(x\right)\right).\end{array}$$

隶属等级 ${\mu }_A\left(x\right)$ 和 ${\mu }_B\left(x\right)$ 被映为新的隶属等级. 函数 $t$ 和 $s$ 称作 $t$ 范数和 $t$ 余范数; 后者也称为 $s$ 范数.

解释 函数 ${\mu }_{A\cup B}$ 和 ${\mu }_{A\cap B}$ 表示隶属真值,它们由隶属真值 ${\mu }_A\left(x\right)$ 和 ${\mu }_B\left(x\right)$ 的聚合得到.

2. $t$ 范数的定义

$t$ 范数是 $\left[0,1\right]$ 中的一个二元运算 $t$ :

$$\begin{array}{}\text{(5.346)}& t:\left[0,1\right]\times \left[0,1\right]\to \left[0,1\right].\end{array}$$

它是对称、结合、单调增加的, 它以 0 作为零元素, 以 1 作为中性元素. 对于 $x,y,z,v,w\in \left[0,1\right]$ ,下列性质成立:

(E1) 交换性

$$\begin{array}{}\text{(5.347a)}& t\left(x,y\right)=t\left(y,x\right).\end{array}$$

(E2) 结合性

$$\begin{array}{}\text{(5.347b)}& t\left(x,t\left(y,z\right)\right)=t\left(t\left(x,y\right),z\right).\end{array}$$

(E3) 与中性元素及零元素的特殊运算

$t\left(x,1\right)=x$ ,并且由于(E1),有 $t\left(1,x\right)=x;t\left(x,0\right)=t\left(0,x\right)=0$ .(5.347c)

(E4) 单调性

如果 $x\le v$ 并且 $y\le w$ ,那么有 $t\left(x,y\right)\le t\left(v,w\right)$ .(5.347d)

3. $s$ 范数的定义

$s$ 范数是 $\left[0,1\right]$ 中的一个二元函数:

$$\begin{array}{}\text{(5.348)}& s:\left[0,1\right]\times \left[0,1\right]\to \left[0,1\right].\end{array}$$

它有下列性质: (E1) 交换性

$$\begin{array}{}\text{(5.349a)}& s\left(x,y\right)=s\left(y,x\right).\end{array}$$

(E2) 结合性

$$\begin{array}{}\text{(5.349b)}& s\left(x,s\left(y,z\right)\right)=s\left(s\left(x,y\right),z\right).\end{array}$$

(E3) 与中性元素及零元素的特殊运算

$$\begin{array}{}\text{(5.349c)}& s\left(x,0\right)=s\left(0,x\right)=x;s\left(x,1\right)=s\left(1,x\right)=1.\end{array}$$

(E4) 单调性

如果 $x\le v$ 并且 $y\le w$ ,那么 $s\left(x,y\right)\le s\left(v,w\right)$ .(5.349d)

借助这些性质可以引进 $t$ 范数的类 $T$ 和 $s$ 范数的类 $S$ . 仔细地研究可给出下列的关系:

$$\begin{array}{}\text{(5.349e)}& min\{x,y\}\ge t\left(x,y\right),\mathrm{\forall }t\in T,\mathrm{\forall }x,y\in \left[0,1\right],\end{array}$$

以及

$$\begin{array}{}\text{(5.349f)}& max\{x,y\}\le s\left(x,y\right),\mathrm{\forall }s\in S,\mathrm{\forall }x,y\in \left[0,1\right].\end{array}$$

5.9.2.2 模糊集的实用聚合运算

1. 两个模糊集的交

两个模糊集 $A$ 和 $B$ 的交 $A\cap B$ 通过在它们的隶属函数 ${\mu }_A\left(x\right)$ 和 ${\mu }_B\left(x\right)$ 上的极小值运算 $min\{\cdot ,\cdot \}$ 定义. 基于先前的要求有

$$\begin{array}{}\text{(5.350a)}& C\text{:=}A\cap B\text{以及}{\mu }_C\left(x\right)\text{:=}min\left\{{\mu }_A\left(x\right),{\mu }_B\left(x\right)\right\},\mathrm{\forall }x\in X\text{,}\end{array}$$

其中

$$\begin{array}{}\text{(5.350b)}& min\{a,b\}\text{:=}\{\begin{array}{ll}a,& a\le b,\\ b,& a>b.\end{array}\end{array}$$

交运算对应于两个隶属函数的 AND 运算 (图 5.72). 隶属函数 ${\mu }_C\left(x\right)$ 定义为 ${\mu }_A\left(x\right)$ 和 ${\mu }_B\left(x\right)$ 的极小值.

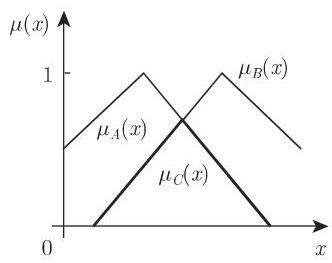
2. 两个模糊集的并

两个模糊集的并 $A\cup B$ 通过在它们的隶属函数 ${\mu }_A\left(x\right)$ 和 ${\mu }_B\left(x\right)$ 上的极大值运算 $max\{\cdot ,\cdot \}$ 定义:

$$\begin{array}{}\text{(5.351a)}& C\text{:=}A\cup B\text{并且}{\mu }_C\left(x\right)\text{:=}max\left\{{\mu }_A\left(x\right),{\mu }_B\left(x\right)\right\},\mathrm{\forall }x\in X\text{,}\end{array}$$

其中

$$\begin{array}{}\text{(5.351b)}& max\{a,b\}\text{:=}\{\begin{array}{ll}a,& a\ge b,\\ b,& a<b.\end{array}\end{array}$$

交运算对应于逻辑 $\mathrm{OR}$ 运算. 图 5.73 表明 ${\mu }_C\left(x\right)$ 是隶属函数 ${\mu }_A\left(x\right)$ 和 ${\mu }_B\left(x\right)$ 的极大值.

$t$ 范数 $t\left(x,y\right)=min\{x,y\}$ 和 $s$ 范数 $s\left(x,y\right)=max\{x,y\}$ 分别定义两个模糊集的交和并 (图 5.74 和图 5.75).

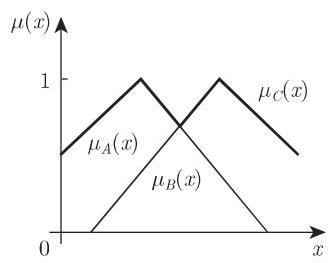
3. 其他聚合

其他聚合有有界聚合、代数聚合、极端和, 以及有界差分、代数积和极端积 (表 5.8).

例如, 代数和定义为

$C\text{:=}A+B$ 并且 ${\mu }_C\left(x\right)\text{:=}{\mu }_A\left(x\right)+{\mu }_B\left(x\right)-{\mu }_A\left(x\right)\cdot {\mu }_B\left(x\right)$ (对所有 $x\in X$ ).(5.352a)

类似地,对于并 (5.531a,5.531b),这个和也属于 $s$ 范数类. 它们都包括在表 5.8 的左边的列中. 表 5.9 给出这些运算在布尔逻辑和模糊逻辑中的比较.

表 $5.8t$ 范数和 $s$ 范数, $p\in \mathbb{R}$

作者	$t$ 范数	$s$ 范数
Zadeh	交: $t\left(x,y\right)=min\{x,y\}$	并: $s\left(x,y\right)=max\{x,y\}$
Lukasiewicz	有界差: $t_b\left(x,y\right)=max\{0,x+y-1\}$	有界和: $s_b\left(x,y\right)=min\{1,x+y\}$
	代数积: $t_a\left(x,y\right)=xy$	代数和: $s_a\left(x,y\right)=x+y-xy$
	极端积: $t_{\mathrm{dp}}\left(x,y\right)=\{\begin{array}{ll}min\{x,y\},& x=1\text{ 或 }y=1,\\ 0,& \text{ 其他 }\end{array}$	极端和: $s_{\mathrm{ds}}\left(x,y\right)=\{\begin{array}{ll}max\{x,y\},& x=0\text{ 或 }y=0,\\ 1,& \text{ 其他 }\end{array}$
Hamacher $\left(p\ge 0\right)$	$t_{\mathrm{h}}\left(x,y\right)=\frac{xy}{p+\left(1-p\right)\left(x+y-xy\right)}$	$s_{\mathrm{h}}\left(x,y\right)=\frac{x+y-xy-\left(1-p\right)xy}{1-\left(1-p\right)xy}$
Einstein	$t_{\mathrm{e}}\left(x,y\right)=\frac{xy}{1+\left(1-x\right)\left(1-y\right)}$	$s_{\mathrm{e}}\left(x,y\right)=\frac{x+y}{1+xy}$
Frank $\left(p>0,p\ne 1\right)$	$t_{\mathrm{f}}\left(x,y\right)={\log }_p\left[1+\frac{\left(p^x-1\right)\left(p^y-1\right)}{p-1}\right]$	$s_{\mathrm{f}}\left(x,y\right)=1-{\log }_p\left[1+\frac{\left(p^{1-x}-1\right)\left(p^{1-y}-1\right)}{p-1}\right]$
Yager $\left(p>0\right)$	$t_{\mathrm{ya}}\left(x,y\right)=1-min\left\{1,{({(1-x)}^p+{(1-y)}^p)}^{1/p}\right\}$	$s_{\mathrm{ya}}\left(x,y\right)=min\left\{1,{(x^p+y^p)}^{1/p}\right\}$
Schweizer $\left(p>0\right)$	$t_{\mathrm{s}}\left(x,y\right)=max{\{0,x^{-p}+y^{-p}-1\}}^{-1/p}$	$s_{\mathrm{s}}\left(x,y\right)=1-max{\{0,{(1-x)}^{-p}+{(1-y)}^p-1\}}^{-1/p}$
Dombi $\left(p>0\right)$	$t_{\mathrm{do}}\left(x,y\right)={\{1+{[{\left(\frac{1-x}{x}\right)}^p+{\left(\frac{1-y}{y}\right)}^p]}^{1/p}\}}^{-1}$	$s_{\mathrm{do}}\left(x,y\right)=1-{\{1+{[{\left(\frac{x}{1-x}\right)}^p+{\left(\frac{y}{1-y}\right)}^p]}^{1/p}\}}^{-1}$
Weber $\left(p\ge -1\right)$	$t_{\mathrm{w}}\left(x,y\right)=max\{0,\left(1+p\right)\left(x+y-1\right)-pxy\}$	$s_{\mathrm{w}}\left(x,y\right)=min\{1,x+y+pxy\}$
Dubois $\left(0\le p\le 1\right)$	$t_{\mathrm{du}}\left(x,y\right)=\frac{xy}{max\{x,y,p\}}$	$s_{\mathrm{du}}\left(x,y\right)=\frac{x+y-xy-min\{x,y,\left(1-p\right)\}}{max\{\left(1-x\right),\left(1-y\right),p\}}$

注: 对于表中所列的 $t$ 范数和 $s$ 范数,有下列顺序: $t_{\mathrm{dp}}\le t_b\le t_{\mathrm{e}}\le t_a\le t_{\mathrm{h}}\le t\le s\le s_h\le s_a\le s_e\le s_b\le s_{\mathrm{ds}}$

算子	布尔逻辑	模糊逻辑 $\left({\mu }_A,{\mu }_B\in \left[0,1\right]\right)$
AND	$C=A\wedge B$	${\mu }_{A\cap B}=min\left\{{\mu }_A,{\mu }_B\right\}$
OR	$C=A\vee B$	${\mu }_{A\cup B}=max\left\{{\mu }_A,{\mu }_B\right\}$
NOT	$C=\mathrm{\neg }A$	${\mu }_A^C=1-{\mu }_A\left({\mu }_A^C\text{ 是 }{\mu }_A\text{ 的补 }\right)$

类似于将和扩充为并运算的概念, 交也可以通过 (例如) 有界积、代数积和极端积来扩充. 例如, 代数积是用下列方式定义的:

$$\begin{array}{}\text{(5.352b)}& C\text{:=}A\cdot B\text{并且}{\mu }_C\left(x\right)\text{:=}{\mu }_A\left(x\right)\cdot {\mu }_B\left(x\right)\text{(对每个}x\in X\text{).}\end{array}$$

类似于交(5.350a,5.350b),它也属于 $t$ 范数类,并且它也可以在表 5.8 的中间一列中找到.

5.9.2.3 补偿算子

有时算子必须介于 $t$ 范数和 $s$ 范数之间; 它们称作补偿算子. $\lambda$ 算子和 $\gamma$ 算子是补偿算子的例子.

1. $\lambda$ 算子

$${\mu }_{A\lambda B}\left(x\right)=\lambda \left[{\mu }_A\left(x\right){\mu }_B\left(x\right)\right]+\left(1-\lambda \right)\left[{\mu }_A\left(x\right)+{\mu }_B\left(x\right)-{\mu }_A\left(x\right){\mu }_B\left(x\right)\right],\lambda \in \left[0,1\right].$$

(5.353)

情形 $\lambda =0$ 方程 (5.353) 产生称作代数和的形式 (表 5.8, $s$ 范数); 它属于 OR 算子.

情形 $\lambda =1$ 方程 (5.353) 产生称作代数积的形式 (表 5.8, $t$ 范数); 它属于 AND 算子.

2. $\gamma$ 算子

$$\begin{array}{}\text{(5.354)}& {\mu }_{A\gamma B}\left(x\right)={\left[{\mu }_A\left(x\right){\mu }_B\left(x\right)\right]}^{1-\gamma }{[1-(1-{\mu }_A\left(x\right))(1-{\mu }_B\left(x\right))]}^{\gamma },\gamma \in \left[0,1\right].\end{array}$$

情形 $\gamma =1$ 方程 (5.354) 产生代数和表达式.

情形 $\gamma =0$ 方程 (5.354) 产生代数积表达式.

将 $\gamma$ 算子应用于任意个模糊集,给出

$$\begin{array}{}\text{(5.355)}& \mu \left(x\right)={[\prod _{i=1}^n{\mu }_i\left(x\right)]}^{1-\gamma }{[1-\prod _{i=1}^n(1-{\mu }_i\left(x\right))]}^{\gamma },\end{array}$$

并且当带权 ${\delta }_i$ 时:

$$\mu \left(x\right)={[\prod _{i=1}^n{\mu }_i{\left(x\right)}^{{\delta }_i}]}^{1-\gamma }{[1-\prod _{i=1}^n{(1-{\mu }_i\left(x\right))}^{{\delta }_i}]}^{\gamma },x\in X,\sum _{i=1}^n{\delta }_i=1,\gamma \in \left[0,1\right].$$

(5.356)

5.9.2.4 扩张原理

上述讨论过将基本的集合运算推广到模糊集. 现在将映射的概念扩充到模糊区域. 概念的基础是不明确语句的接受等级. 经典的映射 $\mathrm{\Phi }:X^n\to Y$ 将一个清晰的函数值 $\mathrm{\Phi }\left(x_1,\cdots ,x_n\right)\in Y$ 指派给点 $\left(x_1,\cdots ,x_n\right)\in X^n$ . 这个映射可以如下地扩充到模糊变量: 模糊映射是 $\hat{\mathrm{\Phi }}:F{\left(X\right)}^n\to F\left(Y\right)$ ,它将一个模糊函数值 $\hat{\mathrm{\Phi }}\left({\mu }_1,\cdots ,{\mu }_n\right)$ 指派给由隶属函数 $\left({\mu }_1,\cdots ,{\mu }_n\right)\in F{\left(X\right)}^n$ 给出的模糊向量变量 $\left(x_1,\cdots ,x_n\right)$ .

5.9.2.5 模糊补

函数 $c:\left[0,1\right]\to \left[0,1\right]$ 称作补函数,如果它具有下列性质: 对于任何 $x,y\in$ $\left[0,1\right]$ ,

(EK1) 边界条件 $c\left(0\right)=1$ 且 $c\left(1\right)=0$ .(5.357a)

(EK2) 单调性 $x<y\Rightarrow c\left(x\right)\ge c\left(y\right)$ .(5.357b)

(EK3) 对合性 $c\left(c\left(x\right)\right)=x$ .(5.357c)

(EK4) 连续性 $c\left(x\right)$ 对每个 $x\in \left[0,1\right]$ 是连续的.(5.357d)

$◼\mathbf{A}$:最常用的 (连续且对合的) 补函数是

$$\begin{array}{}\text{(5.358)}& c\left(x\right)\text{:=}1-x.\end{array}$$

$◼\mathbf{B}$: 其他连续且对合的补函数是菅野 (Sugeno) 补:

$$c_{\lambda }\left(x\right)\text{:=}\left(1-x\right){(1+\lambda x)}^{-1},\lambda \in \left(-1,\mathrm{\infty }\right),$$

以及耶格尔 (Yager) 补:

$$c_p\left(x\right)\text{:=}{(1-x^p)}^{1/p},p\in \left(0,1\right).$$