19.4.1 初值问题

下面讨论求解初值问题的基本方法.

$$\begin{array}{}\text{(19.93)}& y^{\prime }=f\left(x,y\right),y\left(x_0\right)=y_0\end{array}$$

在选定的插值节点集 $x_i$ 上求解未知函数 $y\left(x\right)$ 的近似值 $y_i$ . 通常考虑预先给定步长 $h$ 的等距插值节点

$$\begin{array}{}\text{(19.94)}& x_i=x_0+ih\left(i=0,1,2,\cdots \right).\end{array}$$

19.4.1.1 欧拉多边形法

初值问题 (19.33) 的积分表达式可由下面的积分给出

$$\begin{array}{}\text{(19.95)}& y\left(x\right)=y_0+{\int }_{x_0}^{x}f\left(x,y\left(x\right)\right)\mathrm{d}x.\end{array}$$

这就是近似的出发点

$$\begin{array}{}\text{(19.96)}& y\left(x_1\right)=y_0+{\int }_{x_0}^{x_0+h}f\left(x,y\left(x\right)\right)\mathrm{d}x\approx y_0+hf\left(x_0,y_0\right)=y_1,\end{array}$$

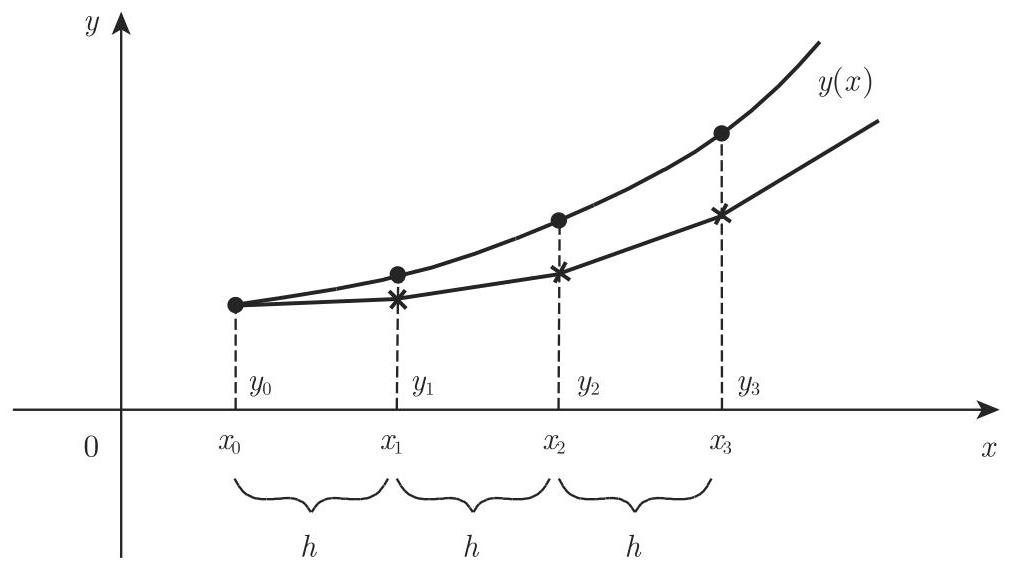
被推广为欧拉折线法或欧拉多边形法

$$\begin{array}{}\text{(19.97)}& y_{i+1}=y_i+hf\left(x_i,y_i\right)\left(i=0,1,2,\cdots ;y\left(x_0\right)=y_0\right).\end{array}$$

几何插值见图 19.5, 对比 (19.96) 与泰勒展开

$$\begin{array}{}\text{(19.98)}& y\left(x_1\right)=y\left(x_0+h\right)=y_0+f\left(x_0,y_0\right)h+\frac{y^{\prime \prime }\left(\xi \right)}{2}{h}^2,\end{array}$$

其中 $x_0<\xi <x_0+h$ ,表明近似值 $y_1$ 具有 $h^2$ 阶误差. 其精度可以通过减小步长 $h$ 来改进. 实际计算表明步长减半可使近似值 $y_i$ 的误差减半.

用欧拉法可以快速看到解曲线的近似形状.

19.4.1.2 龙格-库塔法

1. 计算格式

方程 $y^{\prime }\left(x\right)=f\left(x,y\right)$ 在每一点 $\left(x_0,y_0\right)$ 确定一个方向,解曲线通过点 $\left(x_0,y_0\right)$ 的切线方向. 在下一个插值点前欧拉法沿着该方向. 龙格-库塔法在点 $\left(x_0,y_0\right)$ 与该曲线下一个可能的点 $\left(x_0+h,y_1\right)$ 之间考虑更多的点,适当选取这些附加点以得到 $y_1$ 更准确的值. 依赖于 “辅助点” 的数目与排列,有不同阶的龙格-库塔法. 这里给出了四阶方法 (参见第 1263 页 19.4.1.5). (欧拉法是一阶龙格-库塔法.)

对从 $x_0$ 到 $x_1=x_0+h$ 这一步,四阶计算格式在 (19.99) 中得到 (19.93) 的 $y_1$ 的近似值. 遵照同样的格式进行下一步.

根据 (19.99) 龙格-库塔法的误差在每一步有 $h^5$ 阶,因此适当选取步长可以得到高精度.(19.99)

$x$	$y$	$k=h\cdot f\left(x,y\right)$
$x_0$	$y_0$	$k_1$
$x_0+h/2$	$y_0+k_1/2$	$k_2$
$x_0+h/2$	$y_0+k_2/2$	$k_3$
$x_0+h$	$y_0+k_3$	$k_4$
$x_1=x_0+h$	$y_1=y_0+\frac{1}{6}\left(k_1+2k_2+2k_3+k_4\right)$

$◼y^{\prime }=\frac{1}{4}\left(x^2+y^2\right)$ ,其中 $y\left(0\right)=0.y\left(0.5\right)$ 由一步确定,即 $h=0.5$ (见下表). 8 位数字的准确值为 0.01041860 .

$x$	$y$	$k=\frac{1}{8}\left(x^2+y^2\right)$
0	0	0
0.25	0	0.00781250
0.25	0.00390625	0.00781441
0.5	0.00781441	0.03125763
0.5	0.01041858

2. 注

(1) 对于特殊的微分方程 $y^{\prime }=f\left(x\right)$ ,龙格-库塔法化为辛普森公式 (参见第 1254 页 19.3.2.3).

(2) 对于大量的积分步, 有时候必须改变步长. 改变步长可由原步长重复加倍的精度检验来决定. 若由单倍步长计算 $y\left(x_0+2h\right)$ 得近似值 $y_2\left(h\right)$ ,而由双倍步长计算得 $y_2\left(2h\right)$ ,则误差 $R_2\left(h\right)=y\left(x_0+h\right)-y_2\left(h\right)$ 的估计为

$$\begin{array}{}\text{(19.100)}& R_2\left(h\right)\approx \frac{1}{15}\left[y_2\left(h\right)-y_2\left(2h\right)\right].\end{array}$$

关于步长改变的文献见 [19.31].

(3) 龙格-库塔法对高阶常微分方程也适用, 见 [19.31]. 高阶常微分方程可写成一阶常微分方程组. 于是根据 (19.99), 尽管微分方程之间相互关联, 计算可以并行进行.

19.4.1.3 多步法

由于我们仅从 $y_i$ 计算 $y_{i+1}$ ,因此欧拉法 (19.97) 与龙格-库塔法 (19.99) 都称为单步法. 一般的线性多步法有如下形式:

---

$$y_{i+k}+{\alpha }_{k-1}{y}_{i+k-1}+{\alpha }_{k-2}{y}_{i+k-2}+\cdots +{\alpha }_1{y}_{i+1}+{\alpha }_0{y}_i$$

---

$$\begin{array}{}\text{(19.101)}& =h\left({\beta }_k{f}_{i+k}+{\beta }_{k-1}{f}_{i+k-1}+\cdots +{\beta }_1{f}_{i+1}+{\beta }_0{f}_i\right),\end{array}$$

适当选取常数 ${\alpha }_i$ 和 ${\beta }_j\left(j=0,1,\cdots ,k;{\alpha }_k=1\right)$ . 若 ${\alpha }_0+{\beta }_0\ne 0$ ,公式 (19.101) 称为 $k$ 步法. 若 ${\beta }_k=0$ ,因为此时 (19.101) 的右端 $f_{i+j}=f\left(x_{i+j},y_{i+j}\right)$ 仅包含已知的值为 $y_i,y_{i+1},\cdots ,y_{i+k-1}$ ,故称为显式的. 若 ${\beta }_k\ne 0$ ,此时 (19.101) 两端都需要求新的值 $y_{i+k}$ ,则称为隐式的.

在 $k$ 步法中, $k$ 个初值 $y_0,y_1,\cdots ,y_{k-1}$ 必须已知. 这些初值可以由单步法求得.

若 (19.93) 中的导数 $y^{\prime }\left(x_i\right)$ 由差分公式代替 (参见第 727 页 9.1.1.5,1.),或 (19.95) 中的积分由求积公式近似 (参见第 1252 页 19.3.1), 则由特殊的多步法来求解初值问题 (19.93).

特殊多步法的例子如下.

1. 中点法则

(19.93) 中的导数 $y^{\prime }\left(x_{i+1}\right)$ 由插值节点 $x_i$ 和 $x_{i+2}$ 之间的割线斜率代替,即

$$\begin{array}{}\text{(19.102)}& y_{i+2}-y_i=2h{f}_{i+1}.\end{array}$$

2. 米尔恩 (Milne) 法则

(19.95) 中的积分由辛普森公式近似

$$\begin{array}{}\text{(19.103)}& y_{i+2}-y_i=\frac{h}{3}\left(f_i+4f_{i+1}+f_{i+2}\right).\end{array}$$

3. 亚当斯-巴什福思 (Adams-Bashforth) 法则

(19.95) 中的积分由基于 $k$ 个插值节点 $x_i,x_{i+1},\cdots ,x_{i+k-1}$ 的拉格朗日插值多项式 (参见第 1277 页 19.6.1.2) 代替. 在 $x_{i+k-1}$ 与 $x_{i+k}$ 之间积分得到

$$y_{i+k}-y_{i+k-1}=\sum _{j=0}^{k-1}\left[{\int }_{x_{i+k-1}}^{x_{i+k}}{L}_j\left(x\right)\mathrm{d}x\right]f\left(x_{i+j},y_{i+j}\right)=h\sum _{j=0}^{k-1}{\beta }_{j}f\left(x_{i+j},y_{i+j}\right).$$

(19.104)

方法 (19.104) 对于 $y_{i+k}$ 是显式的. 系数 ${\beta }_j$ 的计算见 [19.4].

19.4.1.4 预估-校正法

实际上, 隐式多步法相较于显式多步法有很大的优越性, 因为在相同的精度下隐式法允许大得多的步长. 但是隐式多步法通常需要求解非线性方程来得到近似值 $y_{i+k}$ . 从 (19.101) 可得如下形式:

$$\begin{array}{}\text{(19.105)}& y_{i+k}=h\sum _{j=0}^k{\beta }_j{f}_{i+j}-\sum _{j=0}^{k-1}{\alpha }_j{y}_{i+j}=F\left(y_{i+k}\right).\end{array}$$

求解方程 (19.105) 需要迭代. 其具体过程是: 根据显式公式确定初值 $y_{i+k}^{\left(0\right)}$ ,称之为预估子, 然后用迭代公式校正

$$\begin{array}{}\text{(19.106)}& y_{i+k}^{(\mu +1)}=F\left(y_{i+k}^{\left(\mu \right)}\right)\left(\mu =0,1,2,\cdots \right),\end{array}$$

这称为由隐式法得到的校正子. 特殊的预估-校正公式有

(1)

$$\begin{array}{}\text{(19.107a)}& y_{i+1}^{\left(0\right)}=y_i+\frac{h}{12}\left(5f_{i-2}-16f_{i-1}+23f_i\right),\end{array}$$$$\begin{array}{}\text{(19.107b)}& y_{i+1}^{(\mu +1)}=y_i+\frac{h}{12}\left(-f_{i-1}+8f_i+5f_{i+1}^{\left(\mu \right)}\right)\left(\mu =0,1,\cdots \right);\end{array}$$

(2)

$$\begin{array}{}\text{(19.108a)}& y_{i+1}^{\left(0\right)}=y_{i-2}+9y_{i-1}-9y_i+6h\left(f_{i-1}+f_i\right),\end{array}$$$$\begin{array}{}\text{(19.108b)}& y_{i+1}^{(\mu +1)}=y_{i-1}+\frac{h}{3}\left(f_{i-1}+4f_i+f_{i+1}^{\left(\mu \right)}\right)\left(\mu =0,1,\cdots \right).\end{array}$$

辛普森公式作为 (19.108b) 中的校正子在数值上是不稳定的, 它可以被替换为

$$\begin{array}{}\text{(19.109)}& y_{i+1}^{(\mu +1)}=0.9y_{i-1}+0.1y_i+\frac{h}{24}\left(0.1f_{i-2}+6.7f_{i-1}+30.7f_i+8.1f_{i+1}^{\left(\mu \right)}\right).\end{array}$$

19.4.1.5 收敛性、相容性、稳定性

1. 整体离散误差和收敛性

单步法可以写成一般形式

$$\begin{array}{}\text{(19.110)}& y_{i+1}=y_i+hF\left(x_i,y_i,h\right)\left(i=0,1,2,\cdots ;y_0\text{ 给定 }\right),\end{array}$$

这里 $F\left(x,y,h\right)$ 称为单步法的增长函数或者顺向函数. 由 (19.110) 得到的近似解依赖于步长 $h$ ,记为 $y\left(x,h\right)$ . 它与初值问题 (19.93) 的准确解 $y\left(x\right)$ 的差被称为整体离散误差 $g\left(x,h\right)$ (见 (19.111)). 若 $p$ 是满足

$$\begin{array}{}\text{(19.111)}& g\left(x,h\right)=y\left(x,h\right)-y\left(x\right)=O\left(h^p\right)\end{array}$$

的最大的自然数,称单步法 (19.110) 是 $p$ 阶收敛的. 公式 (19.111) 表明,若 $h\to 0$ , 步长 $h=\frac{x-x_0}{n}$ ,对于初值问题区域内的每一 $x$ ,近似解 $y\left(x,h\right)$ 收敛到准确解 $y\left(x\right)$ .

| 欧拉法 (19.97) 有一阶收敛性 $p=1$ . 对于龙格-库塔法 (19.99) 则有 $p=4$ .

2. 局部离散误差与相容性

根据 (19.111),收敛阶表明近似解 $y\left(x,h\right)$ 逼近准确解 $y\left(x\right)$ 的好坏程度. 此外, 一个有趣的问题是增长函数 $F\left(x,y,h\right)$ 逼近导数 $y^{\prime }=f\left(x,y\right)$ 的程度. 为此目的, 引进所谓局部离散误差 $l\left(x,h\right)$ (见 (19.112)). 若 $p$ 是满足

$$\begin{array}{}\text{(19.112)}& l\left(x,h\right)=\frac{y\left(x+h\right)-y\left(x\right)}{h}-F\left(x,y,h\right)=O\left(h^p\right)\end{array}$$

的最大的自然数,则称单步法 (19.110) 是 $p$ 阶相容的.

由 (19.112) 直接得到对相容的单步法

$$\begin{array}{}\text{(19.113)}& \underset{h\to 0}{lim}F\left(x,y,h\right)=f\left(x,y\right).\end{array}$$

$◼$ 欧拉法 (19.97) 有一阶相容性 $p=1$ . 龙格-库塔法 (19.99) 则有四阶相容性 $p=4$ .

3. 对初值扰动的稳定性

单步法在实施过程中,舍入误差 $O\left(1/h\right)$ 加到整体离散误差 $O\left(h^p\right)$ 上. 因此我们需要选择一个不太小的有限步长 $h>0$ . 在初值扰动或者 $x_i\to \mathrm{\infty }$ 时数值解 $y_i$ 如何表现也是一个重要的问题.

在常微分方程理论下, 如果

$$\begin{array}{}\text{(19.114)}& \left|\tilde{y}\left(x\right)-y\left(x\right)\right|\le \left|{\tilde{y}}_0-y_0\right|,\end{array}$$

则称初值问题 (19.93) 关于初值扰动是稳定的. 这里 $\tilde{y}\left(x\right)$ 为 (19.93) 关于扰动初值 ${\tilde{y}}_0\left(x_0\right)={\tilde{y}}_0$ 的解. 估计 (19.114) 告诉我们,解的差的绝对值不大于初值的扰动.

一般地, 由于 (19.114) 难以检验, 因此仅考虑线性试验问题

$$\begin{array}{}\text{(19.115)}& y^{\prime }=\lambda y\text{,其中}y\left(x_0\right)=y_0\left(\lambda \le 0\text{为常数}\right)\end{array}$$

用于这一特殊初值问题的单步法是稳定的. 若用一个步长为 $h>0$ 的相容的方法求解上述线性试验问题 (19.115), 得到的近似解满足条件

$$\begin{array}{}\text{(19.116)}& \left|y_i\right|\le \left|y_0\right|\end{array}$$

则称此法对初值扰动是绝对稳定的.

应用欧拉多边形法求解方程 (19.115) 得到解 $y_{i+1}=\left(1+\lambda h\right)y_i\left(i=0,1,\cdots \right)$ . 显然,若 $\left|1+\lambda h\right|\le 1$ ,则 (19.116) 成立,因此步长必须满足 $-2\le \lambda h\le 0$ .

4. 刚性微分方程组

包括化学动力学问题在内的许多应用问题, 可以归结为这样的微分方程, 其解由递减收敛到零的不同的指数项组成. 这些方程称为刚性微分方程. 例如

$$\begin{array}{}\text{(19.117)}& y\left(x\right)=C_1{\mathrm{e}}^{{\lambda }_{1}x}+C_2{\mathrm{e}}^{{\lambda }_{2}x}\left(C_1,C_2,{\lambda }_1,{\lambda }_2\text{ 为常数 }\right),\end{array}$$

其中 ${\lambda }_1<0,{\lambda }_2<0$ 而且 $\left|{\lambda }_1\right|<<\left|{\lambda }_2\right|$ ,例如 ${\lambda }_1=-1,{\lambda }_2=-1000$ . 含 ${\lambda }_2$ 的项对解函数并无显著影响,但在数值方法中影响步长 $h$ 的选取. 在这种情况下,选取适当的数值方法特别重要 (见 [19.29], [19.6]).