Appearance
2.7.3 振动的描述
2.7.3.1 问题表述
在工程和物理中常常会遇到如下由时间决定的量
也称之为正弦量, 它们对时间的依赖产生谐振荡. 如图 2.39 所示, 式 (2.136) 是一般正弦曲线.
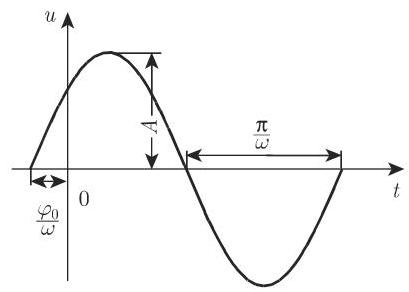
一般正弦曲线与简单正弦曲线
a) 振幅,即曲线上的点与时间轴
b) 周期
c) 初始角
量
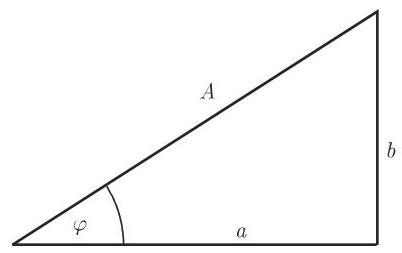
其中
2.7.3.2 振动的叠加
振动叠加中最简单的情况是两个具有相同频率的振动叠加, 得到的仍是具有相同频率的谐振荡:
其中
此处
几个具有相同频率的正弦函数的线性组合也可能产生具有相同频率的一般正弦函数 (谐振荡):
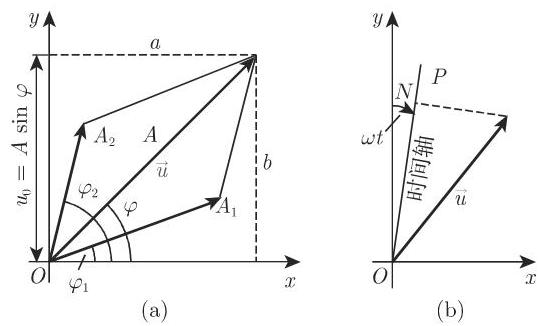
2.7.3.3 振动的向量图
一般正弦曲线 (2.136),(2.137) 可由极坐标
给定时间
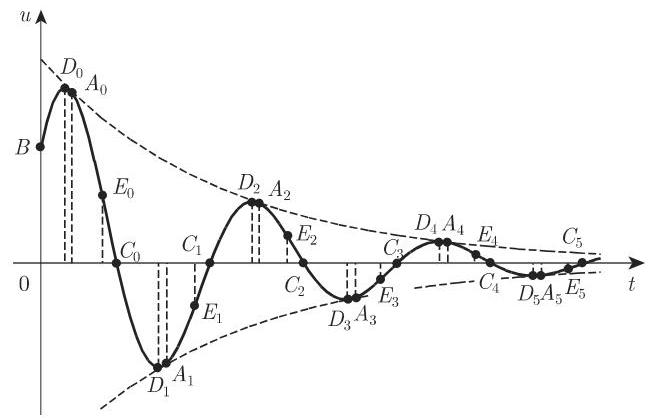
2.7.3.4 振荡的阻尼
函数
产生一阻尼振荡曲线(图 2.42).
随着曲线渐近地趋近
相交, 与坐标轴的交点
当
阻尼的对数衰减率