3.5.2 平面解析几何

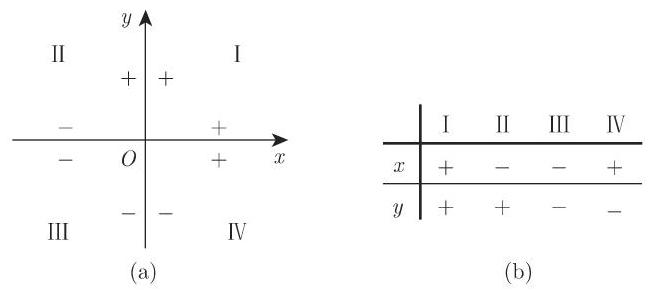
3.5.2.1 基本概念、平面坐标系

平面的每个点 $P$ 的位置可以用任意一个坐标系给出. 确定点的位置的数称为坐标. 大多数情况下使用笛卡儿坐标和极坐标.

1. 笛卡儿坐标

点 $P$ 的笛卡儿坐标是在已给的确定尺度下该点到两个相互垂直的坐标轴的符号距离 (图 3.120). 坐标轴的交点 $O$ 称为原点. 水平坐标轴称为横轴,通常为 $x$ 轴, 垂直坐标轴称为纵轴,通常为 $y$ 轴.

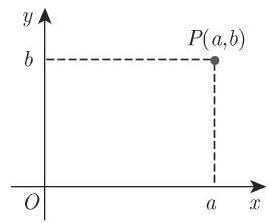
在这些轴上给定了正向: 通常 $x$ 轴的正向朝右, $y$ 轴的正向朝上. 点 $P$ 的坐标的正负取决于该点在哪半轴上的投影 (图 3.121). 坐标 $x$ 和 $y$ 分别称为点 $P$ 的横坐标和纵坐标. 具有横坐标 $a$ 和纵坐标 $b$ 的点记作 $P\left(a,b\right).x,y$ 平面被坐标轴分成四个象限 I, II, III和 IV (图 3.121(a)).

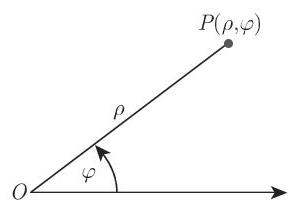
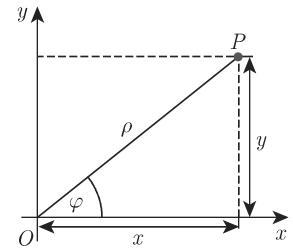
2. 极坐标

点 $P$ 的极坐标 (图 3.122) 是极径 $\rho$ ,即该点到一个给定的极点 $O$ 的距离,以及极角 $\phi$ ,即直线 $OP$ 与一条给定的穿过极点的射线 (极轴)之间的夹角. 极点也称为原点. 如果从极轴出发按逆时针度量则极角为正的, 否则为负.

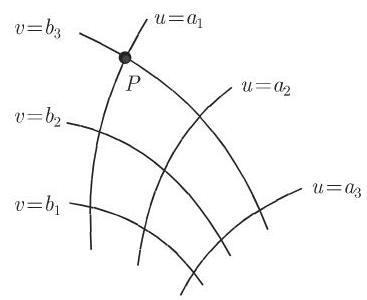
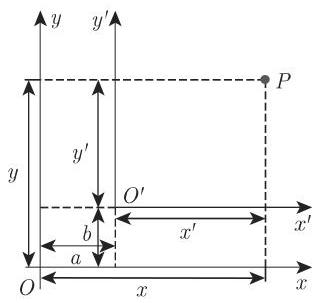
3. 曲线坐标系

这一坐标系由平面上两个单参数曲线族, 即坐标曲线族 (图 3.123) 构成. 通过平面上的每一点恰好有两个族中一条曲线. 它们在该点彼此相交. 对应于该点的参数是它的曲线坐标. 在图 3.123 中点 $P$ 具有曲线坐标 $u=a_1$ 和 $v=b_3$ . 在笛卡儿坐标系中, 坐标曲线是平行于坐标轴的直线; 在极坐标系中, 坐标曲线是以极点为圆心的同心圆和从极点发出的射线.

3.5.2.2 坐标变换

在将一个笛卡儿坐标系变换成另外一个笛卡儿坐标系时, 坐标将按确定的法则发生改变.

1. 坐标轴的平移

将横坐标轴移动 $a$ 单位,纵坐标轴移动 $b$ 单位 (图 3.124). 假设点 $P$ 在平移前具有坐标 $x,y$ ,之后具有坐标 $x^{\prime },y^{\prime }$ . 新原点 $O^{\prime }$ 的旧坐标是 $a,b$ . 新旧坐标之间的关系如下:

$$\begin{array}{}\text{(3.286a)}& x=x^{\prime }+a,y=y^{\prime }+b,\end{array}$$$$\begin{array}{}\text{(3.286b)}& x^{\prime }=x-a,y^{\prime }=y-b.\end{array}$$

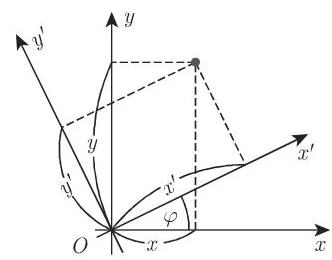
2. 坐标轴的旋转

将坐标轴旋转一个角度 $\phi$ (图 3.125),得到如下的坐标变换:

$$x^{\prime }=x\cos \phi +y\sin \phi ,$$$$\begin{array}{}\text{(3.287a)}& y^{\prime }=-x\sin \phi +y\cos \phi ,\end{array}$$$$x=x^{\prime }\cos \phi -y^{\prime }\sin \phi ,$$$$\begin{array}{}\text{(3.287b)}& y=x^{\prime }\sin \phi +y^{\prime }\cos \phi .\end{array}$$

属于 (3.287a) 的矩阵

$$\mathbf{D}=\left(\begin{array}{cc}\cos \phi & \sin \phi \\ -\sin \phi & \cos \phi \end{array}\right)\text{ 用于 }\left(\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\mathbf{D}\left(\begin{array}{l}x\\ y\end{array}\right)\text{ 和 }\left(\begin{array}{l}x\\ y\end{array}\right)={\mathbf{D}}^{-1}\left(\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right)$$

(3.287c)

称为旋转矩阵.

一般来说, 一个笛卡儿坐标系到另一个笛卡儿坐标系的变换可以分作两步: 坐标轴的平移和旋转.

评论 利用这里讨论的所谓坐标变换虽然改变了坐标系, 但所表示的对象仍然处在它的位置. 相比之下, 利用所谓的几何变换将改变对象, 但坐标系却仍处在它的位置而不发生改变.

在第 308 页 3.5.4.1, 我们用

$$\begin{array}{}\text{(3.288)}& \left(\begin{array}{l}{x}_P^{\prime }\\ y_P^{\prime }\end{array}\right)=\mathbf{R}\left(\begin{array}{l}{x}_P\\ y_P\end{array}\right)\end{array}$$

刻画一个对象的旋转,其中 $\mathbf{R}$ 是旋转矩阵. $\mathbf{D}$ 和 $\mathbf{R}$ 之间存在关系

$$\begin{array}{}\text{(3.289)}& \mathbf{R}={\mathbf{D}}^{-1}.\end{array}$$

3. 笛卡儿坐标与极坐标之间的变换

假设原点与极点重合并且横坐标轴与极轴重合 (图 3.126), 则有

$$\begin{array}{}\text{(3.290a)}& x=\rho \left(\phi \right)\cos \phi ,y=\rho \left(\phi \right)\sin \phi \left(-\pi <\phi \le \pi ,\rho \ge 0\right);\end{array}$$$$\begin{array}{}\text{(3.290b)}& \rho =\sqrt{x^2+y^2},\end{array}$$$$\begin{array}{}\text{(3.290c)}& \phi =\{\begin{array}{ll}\arctan \frac{y}{x}+\pi ,& x<0,\\ \arctan \frac{y}{x},& x>0,\\ \frac{\pi }{2},& x=0,y>0,\\ -\frac{\pi }{2},& x=0,y<0,\\ \text{ 求首次,}& x=y=0.\end{array}\end{array}$$

3.5.2.3 平面上的特殊点

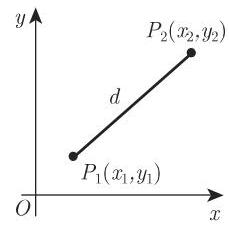
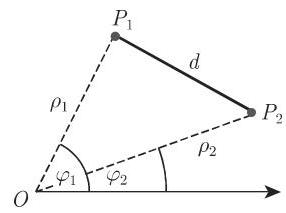
1. 两点之间的距离

如果在笛卡儿坐标系中给定两点 $P_1\left(x_1,y_1\right)$ 和 $P_2\left(x_2,y_2\right)$ (图 3.127),则它们的距离是

$$\begin{array}{}\text{(3.291)}& d=\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}.\end{array}$$

如果它们由极坐标给出为 $P_1\left({\rho }_1,{\phi }_1\right)$ 和 $P_2\left({\rho }_2,{\phi }_2\right)$ (图 3.128),则它们的距离是

$$\begin{array}{}\text{(3.292)}& d=\sqrt{{\rho }_1^2+{\rho }_2^2-2{\rho }_1{\rho }_2\cos \left({\phi }_2-{\phi }_1\right)}.\end{array}$$

2. 质心坐标

具有质量 $m_i\left(i=1,2,\cdots ,n\right)$ 的质点系 $M_i\left(x_i,y_i\right)$ 的质心坐标(x, y)由下列公式计算:

$$\begin{array}{}\text{(3.293)}& x=\frac{\sum m_i{x}_i}{\sum m_i},y=\frac{\sum m_i{y}_i}{\sum m_i}.\end{array}$$

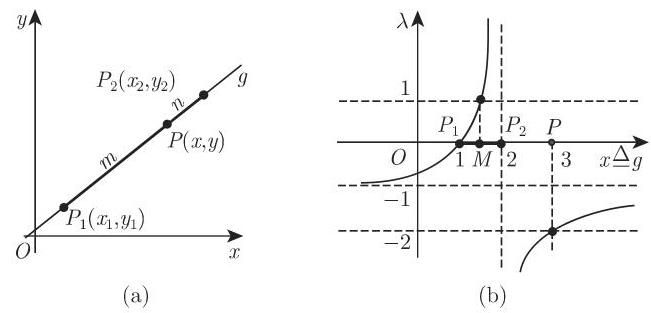
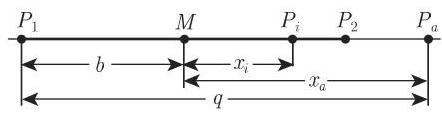
3. 线段的分割

(1) 定比分割 线段 $\overline{P_1{P}_2}$ 的具有分割比 $\frac{\overline{P_{1}P}}{\overline{P{P}_2}}=\frac{m}{n}=\lambda$ 点 $P$ 的坐标由公式

$$\begin{array}{}\text{(3.294a)}& x=\frac{n{x}_1+m{x}_2}{n+m}=\frac{x_1+\lambda x_2}{1+\lambda },\end{array}$$$$\begin{array}{}\text{(3.294b)}& y=\frac{n{y}_1+m{y}_2}{n+m}=\frac{y_1+\lambda y_2}{1+\lambda }\end{array}$$

计算. 对于线段 $\overline{P_1{P}_2}$ 的中点 $M$ ,因为 $\lambda =1$ ,有

$$\begin{array}{}\text{(3.294c)}& x=\frac{x_1+x_2}{2},\end{array}$$$$\begin{array}{}\text{(3.294d)}& y=\frac{y_1+y_2}{2}.\end{array}$$

可以定义 $\overline{P_{1}P}$ 和 ${\overline{PP}}_2$ 的符号. 它们的符号的正负依赖于它们的方向是否与 $\overline{P_1{P}_2}$ 一致. 因此在情形 $\lambda <0$ 下,公式 (3.294a, b) 得到线段 $\overline{P_1{P}_2}$ 之外的一点. 这称为外分.

如果 $P$ 在线段 $\overline{P_1{P}_2}$ 之内,它称为内分. 我们定义

a) 如果 $P=P_1$ ,则 $\lambda =0$ ,

b) 如果 $P=P_2$ ,则 $\lambda =\mathrm{\infty }$ ,

c) 如果 $P$ 是直线 $g$ 的一个无穷远点或反常点,即如果 $P$ 在 $g$ 上距离 $\overline{P_1{P}_2}$ 无穷远,则 $\lambda =-1$ .

图 3.129(b) 显示的是 $\lambda$ 的形状.

对于一点 $P$ ,如果 $P_2$ 是线段 $\overline{P_{1}P}$ 的中点,则成立有 $\lambda =\frac{\overline{P_{1}P}}{\overline{P{P}_2}}=-2$ .

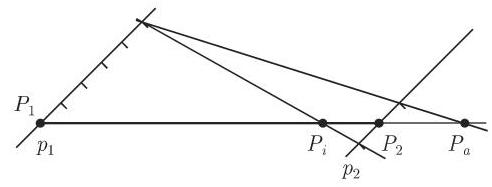
(2) 调和分割 如果一个线段的内分和外分具有相同的绝对值 $\left|\lambda \right|$ ,则产生调和分割. $P_i$ 和 $P_a$ 分别表示内分点和外分点, ${\lambda }_i$ 和 ${\lambda }_a$ 分别表示内分比和外分比. 则

$$\begin{array}{}\text{(3.295a)}& \frac{\overline{P_1{P}_i}}{\overline{P_i{P}_2}}={\lambda }_i=\frac{\overline{P_1{P}_a}}{\overline{P_a{P}_2}}=-{\lambda }_a\end{array}$$

或

$$\begin{array}{}\text{(3.295b)}& {\lambda }_i+{\lambda }_a=0.\end{array}$$

如果 $M$ 表示线段 $\overline{P_1{P}_2}$ 的中点,它与 $P_1$ 的距离是 $b$ (图 3.130), $P_i$ 和 $P_a$ 与 $M$ 的距离分别记作 $x_i$ 和 $x_a$ ,则

$$\begin{array}{}\text{(3.296)}& \frac{b+x_i}{b-x_i}=\frac{x_a+b}{x_i-b}\text{ 或 }\frac{x_i}{b}=\frac{b}{x_a},\text{ 即,}{x}_i{x}_a=b^2.\end{array}$$

名称调和分割与调和平均有关. 在图 3.131 中,对于 $\lambda =5:1$ 表示了调和分割, 与图 3.14 类似. 根据 (3.295a),线段 $\overline{P_1{P}_i}=p$ 和 $\overline{P_1{P}_a}=q$ 的调和平均 $r$ 与第 25 页 (1.67b) 一致, 等于

$$\begin{array}{}\text{(3.297)}& r=\frac{2pq}{p+q}=2b\text{ (参见图 3.132). }\end{array}$$

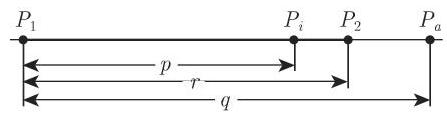
(3) 黄金分割 一线段 $a$ 的黄金分割是将它分成两部分 $x$ 和 $a-x$ 使得 $x$ 部分与整个线段和 $a-x$ 部分与 $x$ 部分具有相同的比:

$$\begin{array}{}\text{(3.298a)}& \frac{x}{a}=\frac{a-x}{x}.\end{array}$$

在此情形, $x$ 是 $a$ 和 $a-x$ 的几何平均 (参见第 2 页 1.1.1.2 中的黄金分割),它成立有

$$\begin{array}{}\text{(3.298b)}& x=\sqrt{a\left(a-x\right)},\end{array}$$$$\begin{array}{}\text{(3.298c)}& x=\frac{a\left(\sqrt{5}-1\right)}{2}\approx 0.618\cdot a.\end{array}$$

该线段的 $x$ 部分可以如图 3.133(a) 所示通过几何作图给出.

评论 1 线段 $x$ 也是具有外接圆半径 $a$ 的正十边形的边长 (参见第 182 页3.1.5.3).

评论 3 下面的几何问题也导致黄金分割方程: 给定一个具有常数边长 $a$ 和变量边长 $a-x$ 的矩形. 求 $x$ 的值使得该矩形的面积 $a\left(a-x\right)$ 等于以 $x$ 为边长的正方形的面积 $x^2$ (图 3.133(b)).

3.5.2.4 面积

1. 凸多边形面积

如果给定凸多边形的顶点 $P_1\left(x_1,y_1\right),P_2\left(x_2,y_2\right),\cdots ,P_n\left(x_n,y_n\right)$ ,则它的面积是

$$S=\frac{1}{2}\left[\left(x_1-x_2\right)\left(y_1+y_2\right)+\left(x_2-x_3\right)\left(y_2+y_3\right)+\cdots +\left(x_n-x_1\right)\left(y_n+y_1\right)\right].$$

(3.299)

如果按反时针顺序计数顶点, 则公式 (3.299) 和 (3.300) 得出正的面积, 否则面积为负.

2. 三角形面积

如果给定三角形的顶点 $P_1\left(x_1,y_1\right),P_2\left(x_2,y_2\right)$ 和 $P_3\left(x_3,y_3\right)$ (图 3.134),则其面积可以用以下公式计算:

$$S=\frac{1}{2}\left|\begin{array}{lll}{x}_1& y_1& 1\\ x_2& y_2& 1\\ x_3& y_3& 1\end{array}\right|=\frac{1}{2}\left[x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right]$$$$\begin{array}{}\text{(3.300)}& =\frac{1}{2}\left[\left(x_1-x_2\right)\left(y_1+y_2\right)+\left(x_2-x_3\right)\left(y_2+y_3\right)+\left(x_3-x_1\right)\left(y_3+y_1\right)\right].\end{array}$$

如果 $\left|\begin{array}{lll}{x}_1& y_1& 1\\ x_2& y_2& 1\\ x_3& y_3& 1\end{array}\right|=0$ 成立,则三点 $P_1,P_2,P_3$ 共线.(3.301)

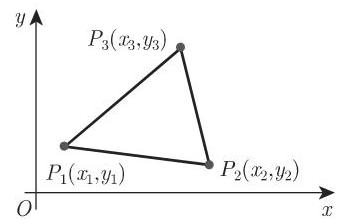
3.5.2.5 曲线方程

对于坐标 $x$ 和 $y$ 而言,方程 $F\left(x,y\right)=0$ 常常对应于一条曲线,它具有如下性质: 这条曲线上的每个点 $P$ 的坐标满足该方程,反之,坐标满足该方程的任何点都在这条曲线上. 这些点的集合也称几何轨迹, 或简称轨迹. 如果平面上没有任何实点满足方程 $F\left(x,y\right)=0$ ,则不存在任何实曲线,这时我们谈论的就是一条虚曲线.

$◼\mathbf{A}$: $x^2+y^2+1=0$ ,

$◼$ $\mathbf{B}:y-\ln \left(1-x^2-\cosh x\right)=0$ .

如果 $F\left(x,y\right)$ 是一个多项式,则相应于方程 $F\left(x,y\right)=0$ 的曲线称为代数曲线, 该多项式的次数也是曲线的次数或阶数(参见第 83 页 2.3.4). 如果曲线方程不能够变形成 $F\left(x,y\right)=0$ ,其中 $F\left(x,y\right)$ 是多项式,则该曲线称为超越曲线.

曲线方程可以在任何一个坐标系中以相同的方式定义. 但本书从现在起只使用笛卡儿坐标系, 除非另作说明.

3.5.2.6 直线

1. 直线方程

每个坐标线性方程都表示一条直线, 反之, 每条直线的方程都是一个坐标线性方程.

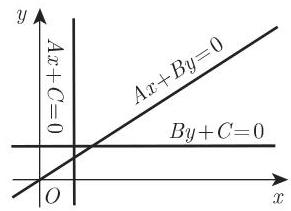
(1) 直线的一般方程

$$\begin{array}{}\text{(3.302)}& Ax+By+C=0\left(A,B,C\text{ 是常数 }\right).\end{array}$$

当 $A=0$ 时直线平行于 $x$ 轴, $B=0$ 时直线平行于 $y$ 轴, $C=0$ 时直线通过原点 (图 3.135).

(2) 直线的斜截式方程 与 $y$ 轴不平行的任何一条直线可以用如下形式的方程表示:

$$\begin{array}{}\text{(3.303)}& y=kx+b\left(k,b\text{ 是常数 }\right).\end{array}$$

量 $k$ 称为是直线的斜率或角系数; 它等于该直线与 $x$ 轴正向夹角的正切 (图 3.136). 直线在 $y$ 轴上的截距是 $b$ . 斜率和 $b$ 的值都可以为负,这取决于直线的位置.

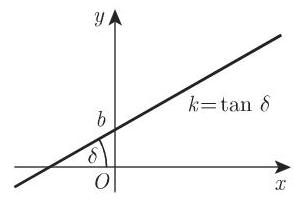
(3) 直线的点斜式方程 以给定方向 (图 3.137) 通过一给定点 $P_1\left(x_1,y_1\right)$ 的直线方程是

$$\begin{array}{}\text{(3.304)}& y-y_1=k\left(x-x_1\right)\text{,其中 }k=\tan \delta .\end{array}$$

(4) 直线的两点式方程 如果给定直线上两点 $P_1\left(x_1,y_1\right)$ 和 $P_2\left(x_2,y_2\right)$ (图 3.138), 则直线的方程是

$$\begin{array}{}\text{(3.305)}& \frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}.\end{array}$$

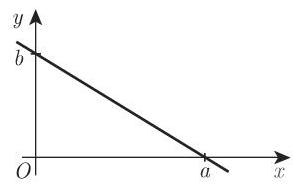
(5) 直线的截距式方程 如果直线在坐标轴上的截距是 $a$ 和 $b$ ,考虑它们的符号, 则直线的方程是 (图 3.139)

$$\begin{array}{}\text{(3.306)}& \frac{x}{a}+\frac{y}{b}=1\end{array}$$

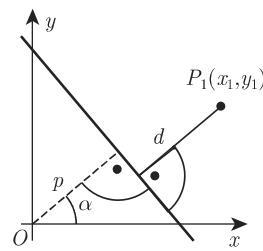
(6) 直线方程的法线式 (黑塞法式) 设 $p$ 是原点到直线的距离, $\alpha$ 是 $x$ 轴与过原点的法线之间的夹角 (图 3.140),其中 $p>0$ ,而 $0\le \alpha <2\pi$ ,则直线方程的黑塞法式为

$$\begin{array}{}\text{(3.307)}& x\cos \alpha +y\sin \alpha -p=0.\end{array}$$

黑塞法式可以从直线的一般方程 (3.302) 通过乘以正规化因子

$$\begin{array}{}\text{(3.308)}& \mu =\pm \frac{1}{\sqrt{A^2+B^2}}\end{array}$$

得到. $\mu$ 的符号必须和 (3.302) 中 $C$ 的符号相反.

(7)直线的极坐标方程(图 3.141) 设 $p$ 是极点到直线的距离 (从极点到直线的法线段), $\alpha$ 是极轴与过极点到直线的法线之间的夹角,则该直线的极坐标方程为

$$\begin{array}{}\text{(3.309)}& \rho =\frac{p}{\cos \left(\phi -\alpha \right)}.\end{array}$$

2. 点到直线的距离

点 $P_1\left(x_1,y_1\right)$ 到一条直线的距离 $d$ (图 3.140) 可以通过将该点的坐标代入黑塞法式 (3.307) 左边得到

$$\begin{array}{}\text{(3.310)}& d=x_1\cos \alpha +y_1\sin \alpha -p.\end{array}$$

如果 $P_1$ 和原点位于直线的两侧,则有 $d>0$ ,否则有 $d<0$ .

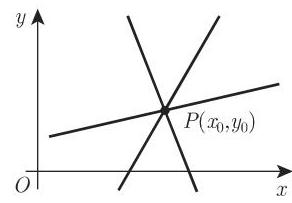
3. 直线的交点

(1) 两条直线的交点 为了得到两条直线的交点坐标 $\left(x_0,y_0\right)$ ,需要解它们的方程构成的方程组. 如果两条直线的方程是

$$\begin{array}{}\text{(3.311a)}& A_{1}x+B_{1}y+C_1=0,A_{2}x+B_{2}y+C_2=0,\end{array}$$

则它们的解为

$$\begin{array}{}\text{(3.311b)}& x_0=\frac{\left|\begin{array}{ll}{B}_1& C_1\\ B_2& C_2\end{array}\right|}{\left|\begin{array}{ll}{A}_1& B_1\\ A_2& B_2\end{array}\right|},y_0=\frac{\left|\begin{array}{ll}{C}_1& A_1\\ C_2& A_2\end{array}\right|}{\left|\begin{array}{ll}{A}_1& B_1\\ A_2& B_2\end{array}\right|}.\end{array}$$

如果 $\left|\begin{array}{ll}{A}_1& B_1\\ A_2& B_2\end{array}\right|=0$ 成立,则两条直线平行. 如果 $\frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}$ 成立,则两条直线重合.

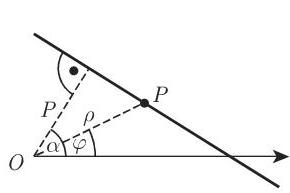
(2)直线束 如果有第三条直线

$$\begin{array}{}\text{(3.312a)}& A_{3}x+B_{3}y+C_3=0\end{array}$$

通过前两条直线的交点 (图 3.142), 则关系

$$\begin{array}{}\text{(3.312b)}& \left|\begin{array}{lll}{A}_1& B_1& C_1\\ A_2& B_2& C_2\\ A_3& B_3& C_3\end{array}\right|=0\end{array}$$

必须满足.

方程

$$\begin{array}{}\text{(3.312c)}& \left(A_{1}x+B_{1}y+C_1\right)+\lambda \left(A_{2}x+B_{2}y+C_2\right)=0\left(-\mathrm{\infty }<\lambda <+\mathrm{\infty }\right)\end{array}$$

给出了通过两条直线 (3.311a) 的交点 $P_0\left(x_0,y_0\right)$ 的全部直线 $(A_{2}x+B_{2}y+C_2=$ 0 除外). (3.312c) 定义了以 $P_0\left(x_0,y_0\right)$ 为中心的平面束. 如果最初的两条直线方程由法线式给出,则 $\lambda =\pm 1$ 时得到交点处角的平分线方程 (图 3.143).

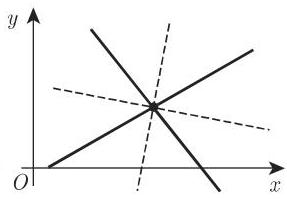
4. 两条直线的夹角

图 3.144 中有两条相交直线. 如果它们的方程由一般式

$$\begin{array}{}\text{(3.313a)}& A_{1}x+B_{1}y+C_1=0\text{ 和 }{A}_{2}x+B_{2}y+C_2=0\end{array}$$

给出,则对于角 $\phi$ 成立有

$$\begin{array}{}\text{(3.313b)}& \tan \phi =\frac{A_1{B}_2-A_2{B}_1}{A_1{A}_2+B_1{B}_2},\end{array}$$$$\begin{array}{}\text{(3.313c)}& \cos \phi =\frac{A_1{A}_2+B_1{B}_2}{\sqrt{A_1^2+B_1^2}\sqrt{A_2^2+B_2^2}},\end{array}$$$$\begin{array}{}\text{(3.313d)}& \sin \phi =\frac{A_1{B}_2-A_2{B}_1}{\sqrt{A_1^2+B_1^2}\sqrt{A_2^2+B_2^2}}.\end{array}$$

借助两条相交直线的斜率 $k_1$ 和 $k_2$ 则有

$$\begin{array}{}\text{(3.313e)}& \tan \phi =\frac{k_2-k_1}{1+k_1{k}_2},\end{array}$$$$\begin{array}{}\text{(3.313f)}& \cos \phi =\frac{1+k_1{k}_2}{\sqrt{1+k_1^2}\sqrt{1+k_2^2}},\end{array}$$$$\begin{array}{}\text{(3.313g)}& \sin \phi =\frac{k_2-k_1}{\sqrt{1+k_1^2}\sqrt{1+k_2^2}},\end{array}$$

这里的角 $\phi$ 是按从第一条直线到第二条直线的逆时针方向度量的.

对于平行直线 (图 3.145(a)) 有等式 $\frac{A_1}{A_2}=\frac{B_1}{B_2}$ 或 $k_1=k_2$ 成立.

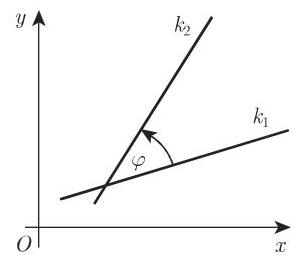
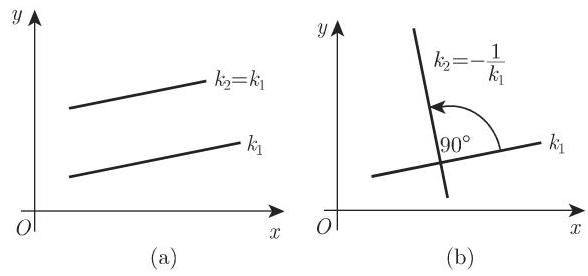
对于垂直 (正交) 直线 (图 3.145(b)) 有 $A_1{A}_2+B_1{B}_2=0$ 或 $k_2=-\frac{1}{k_1}$ 成立.

3.5.2.7 圆

1. 圆的定义

与给定的点具有相同的给定距离的点的轨迹称为圆. 给定的距离称为该圆的半径而给定的点称为该圆的圆心.

2. 圆的笛卡儿坐标方程

当圆心在原点时 (图 3.146(a)), 圆的笛卡儿坐标方程为

$$\begin{array}{}\text{(3.314a)}& x^2+y^2=R^2.\end{array}$$

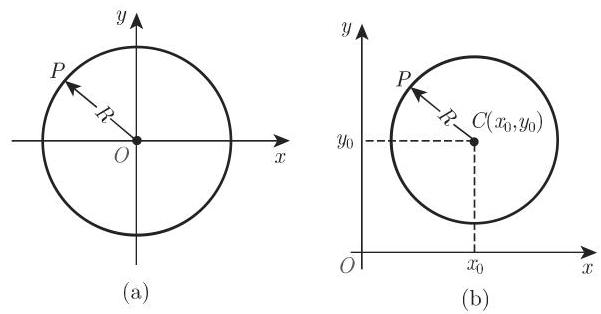
如果圆心在点 $C\left(x_0,y_0\right)$ (图 3.146(b)),则方程为

$$\begin{array}{}\text{(3.314b)}& {(x-x_0)}^2+{(y-y_0)}^2=R^2.\end{array}$$

一般的二次方程

$$\begin{array}{}\text{(3.315a)}& a{x}^2+2bxy+c{y}^2+2dx+2ey+f=0\end{array}$$

只有当 $b=0$ 和 $a=c$ 时才成为圆的方程. 在此情形该方程总能变换成形式

$$\begin{array}{}\text{(3.135b)}& x^2+y^2+2mx+2ny+q=0.\end{array}$$

对于该圆的半径和圆心坐标有下列等式成立:

$$\begin{array}{}\text{(3.316a)}& R=\sqrt{m^2+n^2-q},\end{array}$$$$\begin{array}{}\text{(3.316b)}& x_0=-m,y_0=-n.\end{array}$$

如果 $q>m^2+n^2$ 成立,则该方程定义了一条虚曲线; 如果 $q=m^2+n^2$ ,则曲线只是单独一个点 $P\left(x_0,y_0\right)$ .

3. 圆的参数表达式

$$\begin{array}{}\text{(3.317)}& x=x_0+R\cos t,y=y_0+R\sin t,\end{array}$$

其中 $t$ 是动半径与 $x$ 轴正向之间的夹角 (图 3.147).

4. 圆的极坐标方程

在与图 3.148 对应的一般情形中, 圆的极坐标方程为

$$\begin{array}{}\text{(3.318a)}& {\rho }^2-2\rho {\rho }_0\cos \left(\phi -{\phi }_0\right)+{\rho }_0^2=R^2.\end{array}$$

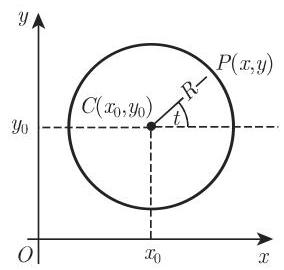
如果圆心在极轴上且圆通过极点 (图 3.149), 则方程具有形式

$$\begin{array}{}\text{(3.318b)}& \rho =2R\cos \phi \end{array}$$

5. 圆的切线

由 (3.314a) 给出的圆在点 $P\left(x_0,y_0\right)$ 处的切线 (图 3.150) 方程具有形式

$$\begin{array}{}\text{(3.319)}& x{x}_0+y{y}_0=R^2.\end{array}$$

3.5.2.8 椭圆

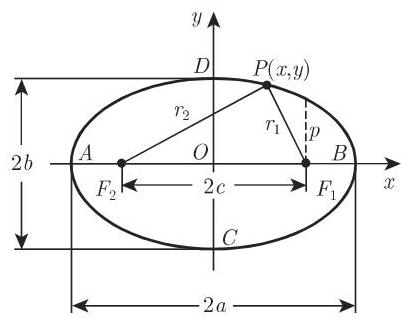
1. 椭圆的要素

在图 3.151 中, $AB=2a$ 是长轴, $CD=2b$ 是短轴, $A,B,C,D$ 是顶点, $F_1,F_2$ 是两侧与中心距离为 $c=\sqrt{a^2-b^2}$ 的焦点, $e=\frac{c}{a}<1$ 是数值离心率, $p=\frac{b^2}{a}$ 是半焦弦, 即过焦点平行于短轴的弦的一半.

2. 椭圆的方程

如果坐标轴与椭圆的长短轴重合, 椭圆的方程具有标准形式. 这一方程以及这一方程的参数形式是

$$\begin{array}{}\text{(3.320a)}& \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\end{array}$$$$\begin{array}{}\text{(3.320b)}& x=a\cos t,y=b\sin t.\end{array}$$

关于用极坐标给出的椭圆方程, 参见第 280 页 3.5.2.11, 6..

3. 椭圆的定义, 焦点性质

椭圆是与两个给定点 (焦点) 的距离之和等于常数 $2a$ 的点的轨迹. 这两段距离也称为椭圆上的点的焦半径,可以由如下等式表示为坐标 $x$ 的函数:

$$\begin{array}{}\text{(3.321)}& r_1=\overline{F_{1}P}=a-ex,r_2=\overline{F_{2}P}=a+ex,r_1+r_2=2a.\end{array}$$

在此以及在下面的笛卡儿坐标公式中, 我们假设椭圆方程是由标准形式给出的.

4. 椭圆的准线

椭圆的准线是与椭圆的短轴平行并和它距离为 $d=a/e$ 的直线 (图 3.152). 椭圆上的每个点 $P\left(x,y\right)$ 满足等式

$$\begin{array}{}\text{(3.322)}& \frac{r_1}{d_1}=\frac{r_2}{d_2}=e\end{array}$$

这一性质也可以当作椭圆的定义.

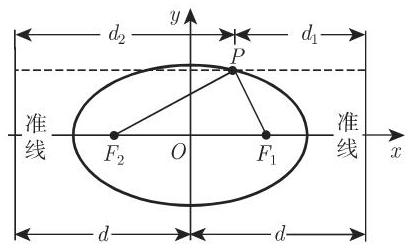
5. 椭圆的直径

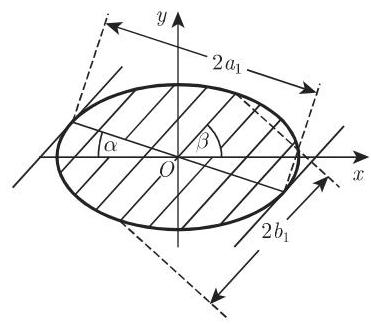
通过椭圆中心的弦称为椭圆的直径. 椭圆的中心也是该直径的中点 (图 3.153). 平行于同一直径的所有弦的中点的轨迹也是一条直径; 它称为前一条直径的共轭直径. 对于两条共轭直径的斜率 $k$ 和 $k^{\prime }$ ,等式

$$\begin{array}{}\text{(3.323)}& k{k}^{\prime }=\frac{-b^2}{a^2}\end{array}$$

成立. 如果 $2a_1$ 和 $2b_1$ 是两条共轭直径的长, $\alpha$ 和 $\beta$ 是两条直径与长轴所夹的锐角, 从而 $k=-\tan \alpha$ 和 $k^{\prime }=\tan \beta$ 成立,则有下面形式的阿波罗尼奥斯定理:

$$\begin{array}{}\text{(3.324)}& a_1{b}_1\sin \left(\alpha +\beta \right)=ab,a_1^2+b_1^2=a^2+b^2.\end{array}$$

6. 椭圆的切线

在点 $P\left(x_0,y_0\right)$ 处椭圆的切线由方程

$$\begin{array}{}\text{(3.325)}& \frac{x{x}_0}{a^2}+\frac{y{y}_0}{b^2}=1\end{array}$$

给出. 椭圆在点 $P$ 处的法线和切线 (图 3.154) 是连接点 $P$ 与焦点的半径所形成的内角和外角的角平分线. 如果有等式

$$\begin{array}{}\text{(3.326)}& A^2{a}^2+B^2{b}^2-C^2=0\end{array}$$

成立,则直线 $Ax+By+C=0$ 是该椭圆的切线.

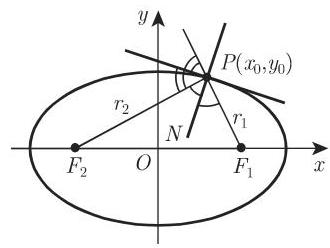
7. 椭圆的曲率半径 (图 3.154)

如果 $u$ 表示切线与连接切点 $P\left(x_0,y_0\right)$ 和焦点的径向量之间的夹角,则曲率半径是

$$\begin{array}{}\text{(3.327)}& R=a^2{b}^2{(\frac{x_0^2}{a^4}+\frac{y_0^2}{b^4})}^{\frac{3}{2}}=\frac{{\left(r_1{r}_2\right)}^{\frac{3}{2}}}{ab}=\frac{p}{{\sin }^{3}u}.\end{array}$$

在顶点 $A$ 和 $B$ 以及 $C$ 和 $D$ ,曲率半径分别是 $R_A=R_B=\frac{b^2}{a}=p$ 和 $R_C=$$R_D=\frac{a^2}{b}.$

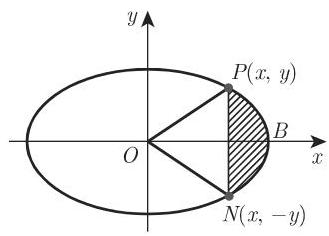
8. 椭圆的面积 (图 3.155)

a) 椭圆:

$$\begin{array}{}\text{(3.328a)}& S=\pi ab.\end{array}$$

b) 椭圆扇形 $BOP$ :

$$\begin{array}{}\text{(3.328b)}& S_{BOP}=\frac{ab}{2}\arccos \frac{x}{a}.\end{array}$$

c) 椭圆弓形 $PBN$ :

$$\begin{array}{}\text{(3.328c)}& S_{PBN}=ab\arccos \frac{x}{a}-xy.\end{array}$$

9. 椭圆的弧长和周长

就像抛物线一样,椭圆上两点 $A$ 和 $B$ 之间的弧长不能用初等方法来计算,而要用到第二类不完全椭圆积分 $E\left(k,\phi \right)$ .

椭圆的周长 (参见第 668 页 8.2.2.2,2.) 可以用具有数值离心率 $e=\frac{\sqrt{a^2-b^2}}{a}$ 和 $\phi =\frac{\pi }{2}$ (对于四分之一周长) 的第二类完全椭圆积分 $E\left(e\right)=E\left(e,\frac{\pi }{2}\right)$ 计算,它等于

$$\begin{array}{}\text{(3.329a)}& L=4aE\left(k,\frac{\pi }{2}\right)=4a{\int }_0^{\pi /2}\sqrt{1-k^2{\sin }^2\psi },\text{ 其中 }k=e=\frac{\sqrt{a^2-b^2}}{a}\end{array}$$

$L=4aE\left(E,\frac{\pi }{2}\right)=4aE\left(e\right)$ 的计算可以借助下面的方法完成:

a) 级数展开

$$L=4aE\left(e\right)=2\pi a\left[1-{\left(\frac{1}{2}\right)}^2{e}^2-{\left(\frac{1\cdot 3}{2\cdot 4}\right)}^2\frac{e^4}{3}-{\left(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\right)}^2\frac{e^6}{5}-\cdots \right],$$

(3.329b)

$$L=\pi \left(a+b\right)\left(1+\frac{{\lambda }^2}{4}+\frac{{\lambda }^4}{64}+\frac{{\lambda }^6}{256}+\frac{25{\lambda }^8}{16384}+\cdots \right)\text{,其中}\lambda =\frac{a-b}{a+b}\text{.}$$

(3.329c)

b) 近似公式

$$\begin{array}{}\text{(3.329d)}& L\approx \pi \left[1,5\left(a+b\right)-\sqrt{ab}\right]\end{array}$$

或

$$\begin{array}{}\text{(3.329e)}& L\approx \pi \left(a+b\right)\frac{64-3{\lambda }^4}{64-16{\lambda }^2}.\end{array}$$

c) 利用第 1424 页关于第二类完全椭圆积分的表 21.9.

d) 确定 (3.329a) 中积分的数值积分方法.

$◼$ 对于 $a=1.5,b=1$ 我们得到下面的 $L$ 的近似值: 根据 (3.329e) 得 $L\approx 7.9327$ , 借助第 1424 页表 21.9 得 $L\approx 7.94$ (参见第 654 页 8.1.4.3, $◼$ ),应用数值积分得更精确的值 $L\approx 7.932721$ .

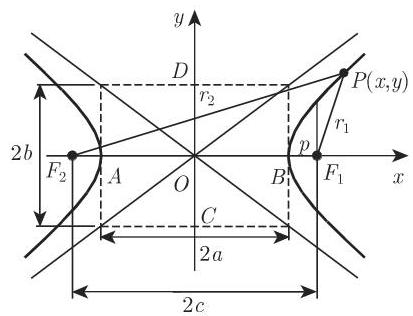
3.5.2.9 双曲线

1. 双曲线的要素

在图 3.156 中, $AB=2a$ 是实轴; $A,B$ 是顶点; $O$ 是中心; $F_1$ 和 $F_2$ 是在实轴上两侧与中心距离为 $c>a$ 的焦点; $CD=2b=2\sqrt{c^2-a^2}$ 是虚轴; $p=\frac{b^2}{a}$ 是双曲线的半焦弦,即垂直于实轴且过焦点的弦的一半; $e=\frac{c}{a}>1$ 是数值离心率.

2. 双曲线的方程

双曲线的标准方程 (即 $x$ 轴与实轴一致) 和参数方程是

$$\begin{array}{}\text{(3.330a)}& \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\end{array}$$$$\begin{array}{}\text{(3.330b)}& x=\pm a\cosh t,y=b\sinh t\left(-\mathrm{\infty }<t<+\mathrm{\infty }\right),\end{array}$$$$\begin{array}{}\text{(3.330c)}& x=\pm \frac{a}{\cos t},y=b\tan t\left(-\frac{\pi }{2}<t<\frac{\pi }{2}\right).\end{array}$$

极坐标的情形见第 280 页 3.5.2.11, 6..

3. 双曲线的定义, 焦点性质

双曲线是与两个给定点 (焦点) 的距离之差等于常数 $2a$ 的点的轨迹. 满足 $r_1-r_2=2a$ 的点属于双曲线的一支 (图 3.156 左边一支),满足 $r_2-r_1=2a$ 的点属于另一支 (图 3.156 右边一支). 这些距离也称为焦半径, 它们可以由下面的公式计算

$$\begin{array}{}\text{(3.331)}& r_1=\pm \left(ex-a\right),r_2=\pm \left(ex+a\right),r_2-r_1=\pm 2a,\end{array}$$

其中右边一支取正号, 左边一支取负号.

在此以及在下面的笛卡儿坐标公式中, 我们假设双曲线方程是由标准形式给出的.

4. 双曲线的准线

双曲线的准线是与实轴垂直并和虚轴距离为 $d=a/c$ 的直线 (图 3.157). 双曲线上的每个点 $P\left(x,y\right)$ 满足等式

$$\begin{array}{}\text{(3.332)}& \frac{r_1}{d_1}=\frac{r_2}{d_2}=e.\end{array}$$

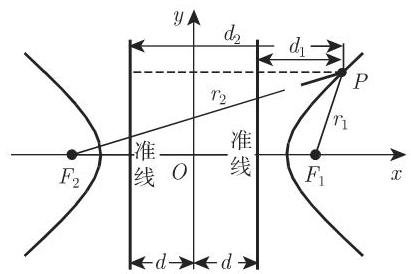
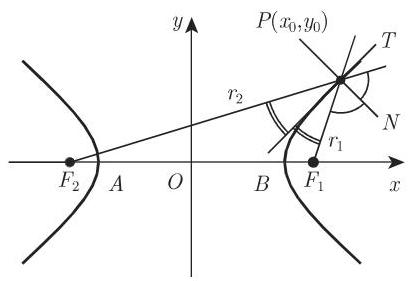
5. 双曲线的切线

在点 $P\left(x_0,y_0\right)$ 处双曲线的切线由方程

$$\begin{array}{}\text{(3.333)}& \frac{x{x}_0}{a_2}-\frac{y{y}_0}{b_2}=1\end{array}$$

给出. 双曲线在点 $P$ 处的法线和切线 (图 3.158) 是连接点 $P$ 与焦点的半径所形成的内角和外角的角平分线. 如果有等式

$$\begin{array}{}\text{(3.334)}& A^2{a}^2-B^2{b}^2-C^2=0\end{array}$$

成立,则直线 $Ax+By+C=0$ 是该椭圆的切线.

6. 双曲线的渐近线

双曲线的渐近线是当 $\left|x\right|\to \mathrm{\infty }$ 时被双曲线的两支无限趋近的直线(图 3.159). (关于渐近线的定义见第 338 页 3.6.1.4) 渐近线的斜率是 $k=\pm \tan \delta =\pm \frac{b}{a}$ . 渐近线的方程是

$$\begin{array}{}\text{(3.335)}& y=\pm \left(\frac{b}{a}\right)x.\end{array}$$

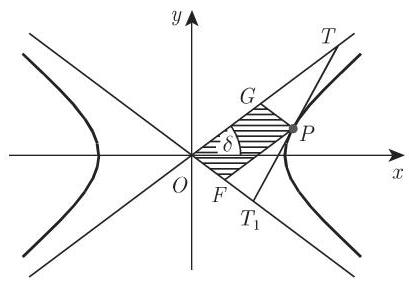
一条切线被渐近线所截,形成双曲线的一个切线段,即线段 $T{T}_1$ (图 3.159). 该切线段的中点是切点 $P$ ,因此有 $TP=T_{1}P$ . 对于任何切点 $P$ 来说,切线与渐近线之间的三角形 $TO{T}_1$ 的面积是相同的,它等于

$$\begin{array}{}\text{(3.336)}& S_{TO{T}_1}=ab.\end{array}$$

对于任何切点 $P$ ,由渐近线和两条过点 $P$ 且平行于渐近线的直线所确定的平行四边形 $OFPG$ 的面积是

$$\begin{array}{}\text{(3.337)}& S_{OFPG}=\frac{ab}{2}.\end{array}$$

7. 共轭双曲线 (图 3.160)

共轭双曲线具有方程

$$\begin{array}{}\text{(3.338)}& \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\text{ 和 }\frac{y^2}{b^2}-\frac{x^2}{a^2}=1,\end{array}$$

其中第二个方程对应的曲线在图 3.160 中用虚线表示. 它们有相同的渐近线, 因此它们之中的一个实轴是另一个的虚轴, 反之亦然.

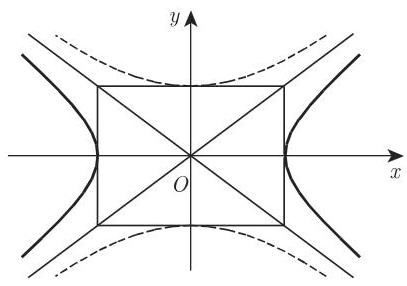
8. 双曲线的直径 (图 3.161)

双曲线的直径是双曲线两支之间过中心的弦, 双曲线的中心也是这些弦的中点. 具有斜率 $k$ 和 $k^{\prime }$ 的两条直径称为是共轭的,如果其中一条属于一个双曲线而另一条属于它的共轭,并且 $k{k}^{\prime }=\frac{b^2}{a^2}$ 成立. 平行于一条直径的弦的中点位于它的共轭直径上 (图 3.161). 两条共轭直径当中符合 $\left|k\right|<\frac{b}{a}$ 的一条与双曲线相交. 如果两条共轭直径的长是 $2a_1$ 和 $2b_1$ ,并且它们与实轴之间所夹的锐角是 $\alpha$ 和 $\beta <\alpha$ ,则有等式

$$\begin{array}{}\text{(3.339)}& a_1^2-b_1^2=a^2-b^2,ab=a_1{b}_1\sin \left(\alpha -\beta \right)\end{array}$$

成立.

9. 双曲线的曲率半径

双曲线在点 $P\left(x_0,y_0\right)$ (图 3.159) 处的曲率半径是

$$\begin{array}{}\text{(3.340a)}& R=a^2{b}^2{(\frac{x_0^2}{a^4}+\frac{y_0^2}{b^4})}^{3/2}=\frac{r_1{r}_2^{3/2}}{ab}=\frac{p}{{\sin }^{3}u},\end{array}$$

其中 $u$ 是切线与连接切点和焦点的径向量之间的夹角. 在顶点 $A$ 和 $B$ 处曲率半径是

$$\begin{array}{}\text{(3.340b)}& R_A=R_B=p=\frac{b^2}{a}.\end{array}$$

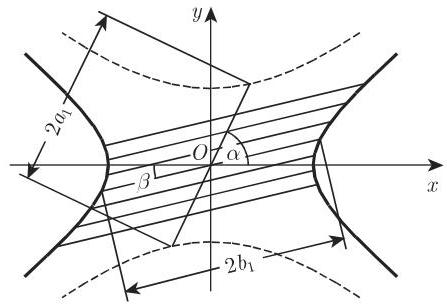
10. 双曲线中的面积(图 3.162)

a) 弓形 $APN$ :

$$\begin{array}{}\text{(3.341a)}& S_{APN}=xy-ab\ln \left(\frac{x}{a}+\frac{y}{b}\right)=xy-ab\mathrm{Arcosh}\frac{x}{a}.\end{array}$$

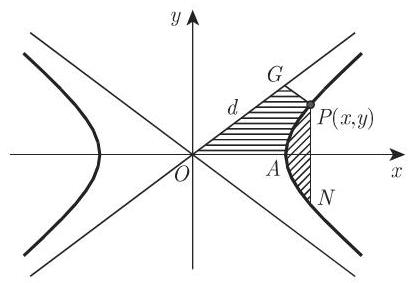
b) 面积 $OAPG$ :

$$\begin{array}{}\text{(3.341b)}& S_{OAPG}=\frac{ab}{4}+\frac{ab}{2}\ln \frac{2d}{c}.\end{array}$$

线段 $PG$ 平行于下面的渐近线, $c$ 是焦距, $d=OG$ .

11. 双曲线的弧长

就像抛物线一样,双曲线上两点 $A$ 和 $B$ 之间的弧长类似于椭圆的弧长 (参见第 270 页 3.5.2.8, 9.), 不能用初等方法来计算, 而要用到第二类不完全椭圆积分 $E\left(k,\phi \right)$ (参见第 654 页 8.1.4.3,2.).

12. 等边双曲线

等边双曲线具有相同长度的轴, 因此它的方程是

$$\begin{array}{}\text{(3.342a)}& x^2-y^2=a^2.\end{array}$$

等边双曲线的渐近线是直线 $y=\pm x$ ; 它们相互垂直. 如果渐近线与坐标轴重合 (图 3.163), 则其方程为

$$\begin{array}{}\text{(3.342b)}& xy=\frac{a^2}{2}.\end{array}$$

3.5.2.10 抛物线

1. 抛物线的要素

在图 3.164 中, $x$ 轴与抛物线的轴重合, $O$ 是抛物线的顶点, $F$ 是抛物线的焦点, 它位于 $x$ 轴上且与原点的距离为 $\frac{p}{2}$ ,其中 $p$ 称为抛物线的半焦弦. 准线记作 $N{N}^{\prime }$ ; 它是在与焦点相对的一侧距原点 $\frac{p}{2}$ 处与 $x$ 轴垂直相交的直线. 半焦弦等于过焦点与轴垂直的弦长的一半. 抛物线的数值离心率等于 1 (参见第 279 页 3.5.2.11, 4.).

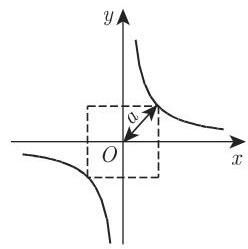
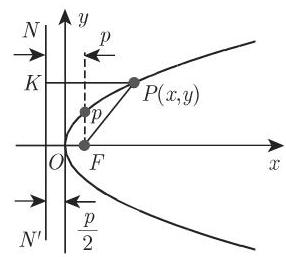
2. 抛物线的方程

如果原点是抛物线的顶点且位于抛物线左侧, $x$ 轴是抛物线的轴,则抛物线方程的标准形式为

$$\begin{array}{}\text{(3.343)}& y^2=2px\end{array}$$

关于极坐标形式的抛物线方程, 见第 280 页 3.5.2.11, 6., 具有垂直轴 (图 3.165) 的抛物线方程为

$$\begin{array}{}\text{(3.344a)}& y=a{x}^2+bx+c.\end{array}$$

由这一形式给出的抛物线的参数为

$$\begin{array}{}\text{(3.344b)}& p=\frac{1}{2\left|a\right|}.\end{array}$$

如果有 $a>0$ ,则抛物线开口朝上,当 $a<0$ 时,开口朝下. 顶点的坐标是

$$\begin{array}{}\text{(3.344c)}& x_0=-\frac{b}{2a},y_0=\frac{4ac-b^2}{4a}.\end{array}$$

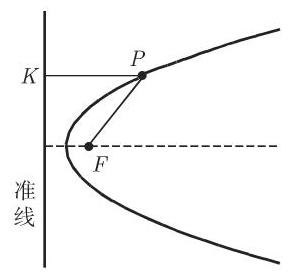
3. 抛物线的性质

(抛物线的定义)抛物线是到给定点 (焦点) 的距离与到给定直线 (准线) 的距离相等的点的轨迹 (图 3.164). 在此以及在下面的笛卡儿坐标公式中, 我们假设抛物线方程是由标准形式给出的, 因此成立等式

$$\begin{array}{}\text{(3.345)}& PF=PK=x+\frac{p}{2},\end{array}$$

其中 $FP$ 是起点在焦点而终点为抛物线上的点的径向量.

4. 抛物线的直径

抛物线的直径是平行于抛物线的轴的直线 (图 3.166). 抛物线的直径平分与其端点处的切线平行的弦 (图 3.166). 设弦的斜率为 $k$ ,则直径的方程是

$$\begin{array}{}\text{(3.346)}& y=\frac{p}{k}.\end{array}$$

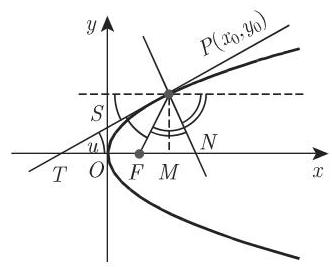
5. 抛物线的切线(图 3.167)

抛物线在点 $P\left(x_0,y_0\right)$ 处的切线方程是

$$\begin{array}{}\text{(3.347)}& y{y}_0=p\left(x+x_0\right).\end{array}$$

切线和法线是从焦点出发的半径与从切点出发的直径之间所夹的角的角平分线. 顶点处的切线,即 $y$ 轴平分切点与切线在抛物线的轴,即 $x$ 轴上的交点之间的切线段:

$$\begin{array}{}\text{(3.348)}& TS=SP,TO=OM=x_0,TF=FP.\end{array}$$

如果

$$p=2bk,$$

则方程 $y=kx+b$ 所表示的直线是抛物线的切线.(3.349)

6. 抛物线的曲率半径

在点 $P\left(x_0,y_0\right)$ 处法线 $PN$ (图 3.167) 的长为 $l_n$ ,则抛物线的曲率半径是

$$\begin{array}{}\text{(3.350a)}& R=\frac{{(p+2x_0)}^{3/2}}{\sqrt{p}}=\frac{p}{{\sin }^{3}u}=\frac{l_n^3}{p^2}\end{array}$$

而在顶点 $O$ 它是

$$\begin{array}{}\text{(3.350b)}& R=p\text{.}\end{array}$$

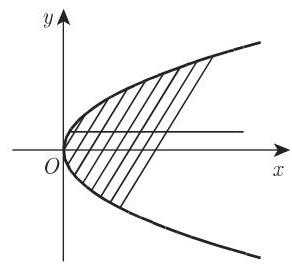
7. 抛物线中的面积(图 3.168)

a) 抛物线弓形 $PON$ :

$$\begin{array}{}\text{(3.351a)}& S_{OPN}=\frac{2}{3}{S}_{MQNP}\left(MQNP\text{ 是平行四边形 }\right).\end{array}$$

b) 面积 $OPR$ (抛物线曲线下的面积)

$$\begin{array}{}\text{(3.351b)}& S_{OPR}=\frac{2xy}{3}.\end{array}$$

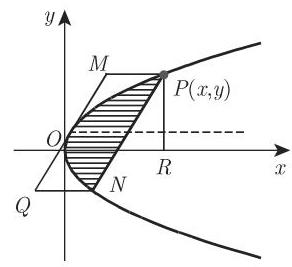
8. 抛物线的弧长

从顶点 $O$ 到点 $P\left(x,y\right)$ 的一段抛物线弧长为

$$\begin{array}{}\text{(3.352a)}& l_{OP}=\frac{p}{2}\left[\sqrt{\frac{2x}{p}\left(1+\frac{2x}{p}\right)}+\ln \left(\sqrt{\frac{2x}{p}}+\sqrt{1+\frac{2x}{p}}\right)\right]\end{array}$$$$\begin{array}{}\text{(3.352b)}& =-\sqrt{x\left(x+\frac{p}{2}\right)}+\frac{p}{2}\mathrm{Arsinh}\sqrt{\frac{2x}{p}}.\end{array}$$

对于 $\frac{x}{y}$ 值较小的情况,可以使用下面的近似公式

$$\begin{array}{}\text{(3.352c)}& l_{OP}\approx y\left[1+\frac{2}{3}{\left(\frac{x}{y}\right)}^2-\frac{2}{5}{\left(\frac{x}{y}\right)}^4\right].\end{array}$$

3.5.2.11 二次曲线 (圆锥曲线)

1. 二次曲线的一般方程

利用二次曲线的一般方程

$$\begin{array}{}\text{(3.353a)}& a{x}^2+2bxy+c{y}^2+2dx+2ey+f=0\end{array}$$

可以定义椭圆, 它的特殊情形 - 圆、双曲线、抛物线或作为奇异圆锥曲线的两条直线.

借助表 3.19 和表 3.20 给出的坐标变换可以将这个方程化简为标准形式.

评论 1 (3.353a) 中的系数并非特殊圆锥曲线中的参数.

评论 2 如果有两个系数 $(a$ 和 $b$ 或 $b$ 和 $c)$ 等于 0,则所需的坐标变换简化为坐标轴的平移.

方程 $c{y}^2+2dx+2ey+f=0$ 可以写成形式 ${(y-y_0)}^2=2p\left(x-x_0\right)$ ;

方程 $a{x}^2+2dx+2ey+f=0$ 可以写成形式 ${(x-x_0)}^2=2p\left(y-y_0\right)$ .

2. 二次曲线的不变量

二次曲线的不变量是如下三个量:

$$\begin{array}{}\text{(3.353b)}& \mathrm{\Delta }=\left|\begin{array}{lll}a& b& d\\ b& c& e\\ d& e& f\end{array}\right|,\delta =\left|\begin{array}{ll}a& b\\ b& c\end{array}\right|,S=a+c.\end{array}$$

它们在坐标系的旋转中保持不变, 即如果在坐标变换后曲线方程具有形式

$$\begin{array}{}\text{(3.353c)}& a^{\prime }{x}^{\prime 2}+2b^{\prime }{x}^{\prime }{y}^{\prime }+c^{\prime }{y}^{\prime 2}+2d^{\prime }{x}^{\prime }+2e^{\prime }{y}^{\prime }+f^{\prime }=0,\end{array}$$

则用新的常数计算 $\mathrm{\Delta },\delta$ 和 $S$ 这三个量将得到同样的值.

量 $\delta$ 和 $\mathrm{\Delta }$			曲线的形状
有心曲线 $\delta \ne 0$	$\delta >0$	$\mathrm{\Delta }\ne 0$	椭圆 a) 当 $\mathrm{\Delta }\cdot S<0$ : 实椭圆, b) 当 $\mathrm{\Delta }\cdot S>0$ : 虚椭圆 **
		$\mathrm{\Delta }=0$	一对具有实公共点的虚 ** 直线
	$\delta <0$	$\mathrm{\Delta }\ne 0$	双曲线
		$\mathrm{\Delta }=0$	一对相交直线
所需坐标变换			变换后方程的标准形式
原点平移到曲线的中心, 其坐标是 $x_0=\frac{be-cd}{\delta },y_0=\frac{bd-ae}{\delta }$ 2. 将坐标轴旋转 $\alpha$ 角, 这里 $\tan 2\alpha =\frac{2b}{a-c}$ $\sin 2\alpha$ 的符号必须和 $2b$ 的符号相一致. 这里新 $x^{\prime }$ 轴的斜率是 $k=\frac{c-a+\sqrt{{(c-a)}^2+4b^2}}{2b}$			$a^{\prime }{x}^{\prime 2}+c^{\prime }{y}^{\prime 2}+\frac{\mathrm{\Delta }}{\delta }=0$
			$a^{\prime }=\frac{a+c+\sqrt{{(a-c)}^2+4b^2}}{2}$ $c^{\prime }=\frac{a+c-\sqrt{{(a-c)}^2+4b^2}}{2}$ ( $a^{\prime }$ 和 $c^{\prime }$ 是二次方程 $u^2-Su+\delta =0$ 的根)

$\ast \mathrm{\Delta },\delta$ 和 $S$ 是(3.353b)中给出的数.

** 该曲线方程对应于一条虚曲线.

3. 二次曲线 (圆锥曲线) 的形状

如果一个对顶直圆锥被一个平面所截, 则导致圆锥曲线. 如果该平面不通过圆锥的顶点, 则结果是一个双曲线、一个抛物线或一个椭圆, 这取决于该平面是否平行于圆锥的两条母线, 一条母线或不平行于圆锥的任何母线. 如果该平面通过顶点, 则结果是一个奇异圆锥曲线,并有 $\mathrm{\Delta }=0$ . 圆柱,即顶点在无穷远处的奇异圆锥的圆锥曲线是平行线. 圆锥曲线的形状可以借助表 3.19 和表 3.20 来确定.

4. 二次曲线的一般性质

到定点 $F$ (焦点) 的距离与到定直线 (准线) 的距离之比为常数 $e$ 的点 (图 3.169) 的轨迹是具有数值离心率 $e$ 的二次曲线. 当 $e<1$ 时为椭圆,当 $e=1$ 时为抛物线, 当 $e>1$ 时为双曲线.

量 $\delta$ 和 $\mathrm{\Delta }$			曲线的形状
抛物曲线 ${}^{\ast },\delta =0$	$\mathrm{\Delta }\ne 0$	抛物线
	$\mathrm{\Delta }=0$	两条直线:	平行直线,当 $d^2-af>0$ , 二重直线,当 $d^2-af=0$ , 虚 ** 直线,当 $d^2-af<0$ .
所需坐标变换			变换后方程的标准形式

$\mathrm{\Delta }\ne 0$

1. 原点平移到抛物线的顶点,其坐标 $x_0$ 和 $y_0$

由方程 $a{x}_0+b{y}_0+\frac{ad+be}{S}=0$ 和 ${y^{\prime }}^2=2p{x}^{\prime }$

$\left(d+\frac{dc-be}{S}\right)x_0+\left(e+\frac{ae-bd}{S}\right)y_0+f=0p=\frac{ae-bd}{S\sqrt{a^2+b^2}}$

定义.

2. 将坐标轴旋转 $\alpha$ 角,

这里 $\tan \alpha =-\frac{a}{b};\sin \alpha$ 的符号必须不同于

$a$ 的符号.

将坐标轴旋转 $\alpha$ 角, $S{y^{\prime }}^2+2\frac{ad+be}{\sqrt{a^2+b^2}}{y}^{\prime }+f=0$ 可以

这里 $\tan \alpha =-\frac{a}{b};\sin \alpha$ 的符号必须不同于 变换成形式

$a$ 的符号. $\left(y^{\prime }-y_0^{\prime }\right)\left(y^{\prime }-y_1^{\prime }\right)=0$ .

$\ast$ 在 $\delta =0$ 的情形,假设系数 $a,b,c$ 都不等于 0 .

** 该曲线方程对应于一条虚曲线.

5. 通过五个点确定一条曲线

过平面上五个给定的点有且仅有一条二次曲线. 如果其中有三个点位于同一条直线上, 则它是奇异或退化圆锥曲线.

6. 二次曲线的极坐标方程

所有二次曲线都可以表示成极坐标方程

$$\begin{array}{}\text{(3.354)}& \rho =\frac{p}{1+e\cos \phi },\end{array}$$

其中 $p$ 是半焦弦, $e$ 是离心率. 这里极点位于焦点处,而极轴从焦点指向较近的顶点. 对于双曲线来说, 这个方程只定义了它的一支.