6.2.2 全微分和高阶微分

6.2.2.1 多元函数全微分的概念

1. 可微性

多元函数 $u=f\left(x_1,x_2,\cdots ,x_i,\cdots ,x_n\right)$ 称为在点 $P_0(x_{10},x_{20},\cdots ,x_{i0},\cdots$ , $x_{n0})$ 可微,若对任意小量 $\mathrm{\Delta }{x}_1,\mathrm{\Delta }{x}_2,\cdots ,\mathrm{\Delta }{x}_i,\cdots ,\mathrm{\Delta }{x}_n$ ,在点 $P(x_{10}+\mathrm{\Delta }{x}_1,x_{20}+$ $\mathrm{\Delta }{x}_2,\cdots ,x_{i0}+\mathrm{\Delta }{x}_i,\cdots ,x_{n0}+\mathrm{\Delta }{x}_n)$ 与在点 $P_0\left(x_{10},x_{20},\cdots ,x_{i0},\cdots ,x_{n0}\right)$ 处函数的全增量

$$\mathrm{\Delta }u=f\left(x_{10}+\mathrm{\Delta }{x}_1,x_{20}+\mathrm{\Delta }{x}_2,\cdots ,x_{i0}+\mathrm{\Delta }{x}_i,\cdots ,x_{n0}+\mathrm{\Delta }{x}_n\right)$$$$\begin{array}{}\text{(6.41a)}& -f\left(x_{10},x_{20},\cdots ,x_{i0},\cdots ,x_{n0}\right)\end{array}$$

与所有变量的偏微分之和

$$\begin{array}{}\text{(6.41b)}& {(\frac{\partial u}{\partial x_1}\mathrm{d}{x}_1+\frac{\partial u}{\partial x_2}\mathrm{d}{x}_2+\cdots +\frac{\partial u}{\partial x_n}\mathrm{d}{x}_n)}_{x_{10},x_{20},\cdots ,x_{n0}}\end{array}$$

相差为距离

$$\begin{array}{}\text{(6.41c)}& \overline{P_{0}P}=\sqrt{\mathrm{\Delta }{x}_1^2+\mathrm{\Delta }{x}_2^2+\cdots +\mathrm{\Delta }{x}_n^2}=\sqrt{\mathrm{d}{x}_1^2+\mathrm{d}{x}_2^2+\cdots +\mathrm{d}{x}_n^2}\end{array}$$

的高阶无穷小.

若多元连续函数的偏导数作为多元函数在一点的邻域内连续, 则该多元函数在这一点可微. 这是可微的充分非必要条件, 事实上, 即使偏导数在一点存在, 函数在该点也未必连续.

2. 全微分

若 $u$ 为可微函数,则和式 (6.41b) 称为函数的全微分,记为

$$\begin{array}{}\text{(6.42a)}& \mathrm{d}u=\frac{\partial u}{\partial x_1}\mathrm{d}{x}_1+\frac{\partial u}{\partial x_2}\mathrm{d}{x}_2+\cdots +\frac{\partial u}{\partial x_n}\mathrm{d}{x}_n.\end{array}$$

由 $n$ 维向量

$$\begin{array}{}\text{(6.42b)}& \mathrm{grad}\underset{―}{\mathbf{u}}={(\frac{\partial u}{\partial x_1},\frac{\partial u}{\partial x_2},\cdots ,\frac{\partial u}{\partial x_n})}^{\mathrm{T}},\end{array}$$$$\begin{array}{}\text{(6.42c)}& \mathbf{d}\underset{―}{\mathbf{r}}={(\mathrm{d}{x}_1,\mathrm{d}{x}_2,\cdots ,\mathrm{d}{x}_n)}^{\mathrm{T}},\end{array}$$

则全微分可以表示为标量积

$$\begin{array}{}\text{(6.42d)}& \mathrm{d}u={\left(\mathrm{grad}\underset{―}{u}\right)}^{\mathrm{T}}\cdot \mathbf{d}\underset{―}{r}.\end{array}$$

(6.42b) 中含 $n$ 个变元的向量为梯度,其定义见 926 页 13.2.2.

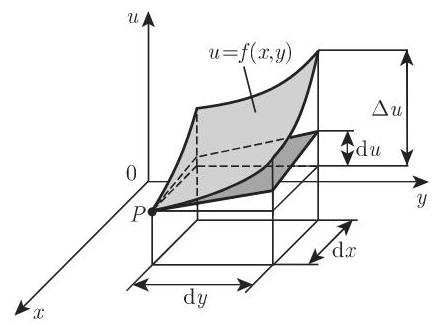
3. 几何表示

二元函数 $u=f\left(x,y\right)$ 在笛卡儿坐标系中表示一曲面,它的全微分的几何意义 (图 6.15): 若 $\mathrm{d}x,\mathrm{d}y$ 是 $x,y$ 的增量,则 $\mathrm{d}u$ 等于切平面 (在同一点) 的竖坐标 (参见第 281 页 3.5.3.1, 3.) 的增量.

由泰勒公式 (参见第 602 页 6.2.2.3, 1.), 可得对二元函数, 有

$$\begin{array}{}\text{(6.43a)}& f\left(x,y\right)=f\left(x_0,y_0\right)+\frac{\partial f}{\partial x}\left(x_0,y_0\right)\left(x-x_0\right)+\frac{\partial f}{\partial y}\left(x_0,y_0\right)\left(y-y_0\right)+R_1.\end{array}$$

忽略掉余项 $R_1$ ,有

$$\begin{array}{}\text{(6.43b)}& u=f\left(x_0,y_0\right)+\frac{\partial f}{\partial x}\left(x_0,y_0\right)\left(x-x_0\right)+\frac{\partial f}{\partial y}\left(x_0,y_0\right)\left(y-y_0\right),\end{array}$$

它给出了曲面 $u=f\left(x,y\right)$ 在点 $P_0\left(x_0,y_0,z_0\right)$ 的切平面方程.

4. 全微分的基本性质

与一元函数中的公式 (6.38) 类似, 全微分关于自变量也具有微分形式不变性.

5. 在误差计算中的应用

在误差计算中,常常使用全微分 $\mathrm{d}u$ 作为 $\mathrm{\Delta }u$ (参见 (6.41a)) 的误差估计 (具体例子参见第 1111 页 16.4.1.3, 5.). 由泰勒公式 (参见第 602 页 6.2.2.3, 1.), 有

$$\begin{array}{}\text{(6.44)}& \left|\mathrm{\Delta }u\right|=\left|\mathrm{d}u+R_1\right|\le \left|\mathrm{d}u\right|+\left|R_1\right|\approx \left|\mathrm{d}u\right|,\end{array}$$

即绝对误差 $\left|\mathrm{\Delta }u\right|$ 可用 $\left|\mathrm{d}u\right|$ 作初步近似,由此 $\mathrm{d}u$ 是 $\mathrm{\Delta }u$ 的线性近似.

6.2.2.2 高阶导数与微分

1. 二阶偏导数、施瓦茨交换定理

多元函数 $u=f\left(x_1,x_2,\cdots ,x_i,\cdots ,x_n\right)$ 的二阶偏导数分两种情况: 一种是对同一个变量的偏导数,如 $\frac{{\partial }^{2}u}{\partial x_1^2},\frac{{\partial }^{2}u}{\partial x_2^2},\cdots$ ; 另一种是对两个变量的偏导数,如 $\frac{{\partial }^{2}u}{\partial x_1\partial x_2}$ , $\frac{{\partial }^{2}u}{\partial x_2\partial x_3},\frac{{\partial }^{2}u}{\partial x_3\partial x_1},\cdots$ . 第二种情况称为混合偏导数. 若在一点混合偏导数连续,则对微分次序中独立的 $x_1,x_2$ ,有

$$\begin{array}{}\text{(6.45)}& \frac{{\partial }^{2}u}{\partial x_1\partial x_2}=\frac{{\partial }^{2}u}{\partial x_2\partial x_1}\text{ (施瓦茨交换定理). }\end{array}$$

类似地,可定义高阶偏导数,如 $\frac{{\partial }^{3}u}{\partial x_1^3},\frac{{\partial }^{3}u}{\partial x\partial y^2},\cdots$ .

2. 一元函数 $y=f\left(x\right)$ 的二阶微分

一元函数 $y=f\left(x\right)$ 的一阶微分的微分称为二阶微分,记为 ${\mathrm{d}}^{2}y,{\mathrm{d}}^{2}f\left(x\right)$ ,其中 ${\mathrm{d}}^{2}y=\mathrm{d}\left(\mathrm{d}y\right)=f^{\prime \prime }\left(x\right)\mathrm{d}{x}^2$ . 仅当 $x$ 为自变量时,才适于采用这样的符号,若 $x$ 由 $x=z\left(v\right)$ 的形式给出,上述符号就不再适用. 类似地可以定义高阶微分. 若变元 $x_1,x_2,\cdots ,x_i,\cdots ,x_n$ 本身是其他变元的函数,可得到更复杂的公式 (参见第 606 页 6.2.4).

3. 二元函数 $u=f\left(x,y\right)$ 的二阶全微分

$$\begin{array}{}\text{(6.46a)}& {\mathrm{d}}^{2}u=\mathrm{d}\left(\mathrm{d}u\right)=\frac{{\partial }^{2}u}{\partial x^2}\mathrm{d}{x}^2+2\frac{{\partial }^{2}u}{\partial x\partial y}\mathrm{d}x\mathrm{d}y+\frac{{\partial }^{2}u}{\partial y^2}\mathrm{d}{y}^2,\end{array}$$

或象征性地写为

$$\begin{array}{}\text{(6.46b)}& {\mathrm{d}}^{2}u={(\frac{\partial }{\partial x}\mathrm{d}x+\frac{\partial }{\partial y}\mathrm{d}y)}^{2}u.\end{array}$$

4. 二元函数的 $n$ 阶全微分

$$\begin{array}{}\text{(6.47)}& {\mathrm{d}}^{n}u={(\frac{\partial }{\partial x}\mathrm{d}x+\frac{\partial }{\partial y}\mathrm{d}y)}^{n}u.\end{array}$$

5. $m$ 元函数 $u=f\left(x_1,x_2,\cdots ,x_m\right)$ 的 $n$ 阶全微分

$$\begin{array}{}\text{(6.48)}& {\mathrm{d}}^{n}u={(\frac{\partial }{\partial x_1}\mathrm{d}{x}_1+\frac{\partial }{\partial x_2}\mathrm{d}{x}_2+\cdots +\frac{\partial }{\partial x_m}\mathrm{d}{x}_m)}^{n}u.\end{array}$$

6.2.2.3 多元函数的泰勒定理

1. 二元函数的泰勒定理

a) 第一种表示形式

$$f\left(x,y\right)=f\left(a,b\right)+{\frac{\partial f\left(x,y\right)}{\partial x}|}_{\left(x,y\right)=\left(a,b\right)}\left(x-a\right)+{\frac{\partial f\left(x,y\right)}{\partial y}|}_{\left(x,y\right)=\left(a,b\right)}\left(y-b\right)$$$$+\frac{1}{2!}\{{\frac{{\partial }^{2}f\left(x,y\right)}{\partial x^2}|}_{\left(x,y\right)=\left(a,b\right)}{(x-a)}^2+{2\frac{{\partial }^{2}f\left(x,y\right)}{\partial x\partial y}|}_{\left(x,y\right)=\left(a,b\right)}\left(x-a\right)\left(y-b\right)$$$$+{\frac{{\partial }^{2}f\left(x,y\right)}{\partial y^2}|}_{\left(x,y\right)=\left(a,b\right)}{(y-b)}^2\}+\frac{1}{3!}\{\cdots \}+\cdots +\frac{1}{n!}\{\cdots \}+R_n,$$

(6.49a)

其中(a, b)是展开式的中心, $R_n$ 是余项. 有时采用简写符号,如把

$${\frac{\partial f\left(x,y\right)}{\partial x}|}_{\left(x,y\right)=\left(x_0,y_0\right)},$$

简记为 $\frac{\partial f}{\partial x}\left(x_0,y_0\right)$ .

(6.49a) 中更高阶的项可以借助下列符号清晰地表示出来:

$$f\left(x,y\right)=f\left(a,b\right)+{\frac{1}{1!}\{(x-a)\frac{\partial }{\partial x}+(y-b)\frac{\partial }{\partial y}\}f(x,y)|}_{\left(x,y\right)=\left(a,b\right)}$$$$+{\frac{1}{2!}{\{(x-a)\frac{\partial }{\partial x}+(y-b)\frac{\partial }{\partial y}\}}^{2}f(x,y)|}_{\left(x,y\right)=\left(a,b\right)}$$$$+{\frac{1}{3!}\{\cdots {\}}^{3}f(x,y)|}_{\left(x,y\right)=\left(a,b\right)}+\cdots +{\frac{1}{n!}\{\cdots {\}}^{n}f(x,y)|}_{\left(x,y\right)=\left(a,b\right)}+R_n.$$

(6.49b)

这种符号形式的意思是: 利用二项式定理后微分符号 $\frac{\partial }{\partial x},\frac{\partial }{\partial y}$ 的幂表示函数 $f\left(x,y\right)$ 的高阶导数,然后让导数在点(a, b)取值.

b) 第二种表示形式

$$f\left(x+h,y+k\right)=f\left(x,y\right)+\frac{1}{1!}\left(\frac{\partial }{\partial x}h+\frac{\partial }{\partial y}k\right)f\left(x,y\right)+\frac{1}{2!}{(\frac{\partial }{\partial x}h+\frac{\partial }{\partial y}k)}^{2}f\left(x,y\right)$$$$+\frac{1}{3!}{(\frac{\partial }{\partial x}h+\frac{\partial }{\partial y}k)}^{3}f\left(x,y\right)+\cdots$$$$\begin{array}{}\text{(6.49c)}& +\frac{1}{n!}{(\frac{\partial }{\partial x}h+\frac{\partial }{\partial y}k)}^{n}f\left(x,y\right)+R_n.\end{array}$$

c) 余项 余项的表达式为

$$\begin{array}{}\text{(6.49d)}& R_n=\frac{1}{\left(n+1\right)!}{(\frac{\partial }{\partial x}h+\frac{\partial }{\partial y}k)}^{n+1}f\left(x+\mathrm{\Theta }h,y+\mathrm{\Theta }k\right)\left(0<\mathrm{\Theta }<1\right).\end{array}$$

2. $m$ 元函数的泰勒公式

用微分符号可类似地表示为

$$f\left(x+h,y+k,\cdots ,t+l\right)$$$$\begin{array}{}\text{(6.50a)}& =f\left(x,y,\cdots ,t\right)+\sum _{i=1}^n\frac{1}{i!}{(\frac{\partial }{\partial x}h+\frac{\partial }{\partial y}k+\cdots +\frac{\partial }{\partial t}l)}^{i}f\left(x,y,\cdots ,t\right)+R_n,\end{array}$$

其中余项可用如下表达式来计算

$$R_n=\frac{1}{\left(n+1\right)!}{(\frac{\partial }{\partial x}h+\frac{\partial }{\partial y}k+\cdots +\frac{\partial }{\partial t}l)}^{n+1}$$$$\begin{array}{}\text{(6.50b)}& \times f\left(x+\mathrm{\Theta }h,y+\mathrm{\Theta }k,\cdots ,t+\mathrm{\Theta }l\right)\left(0<\mathrm{\Theta }<1\right).\end{array}$$